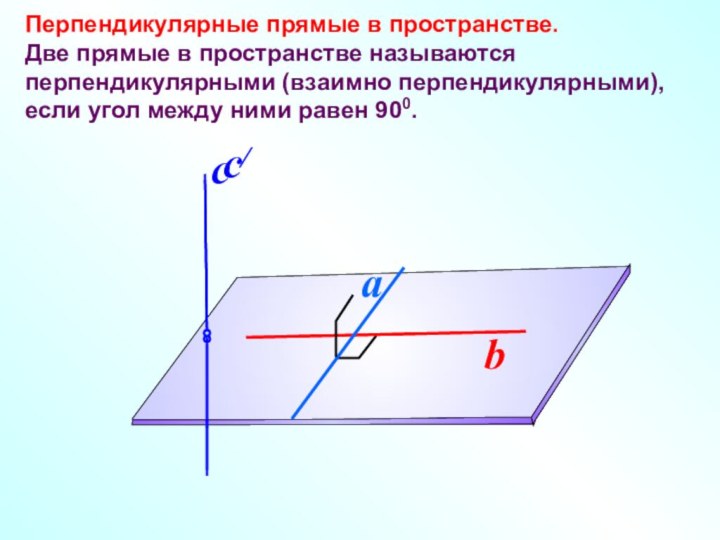
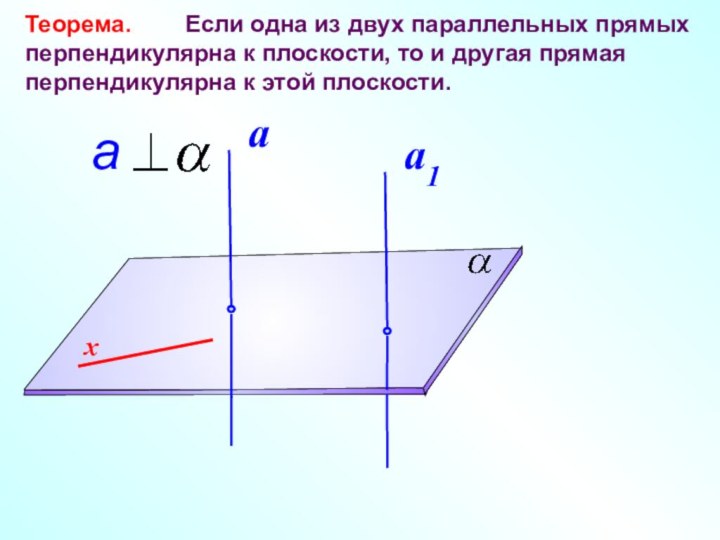
прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол
между ними равен 900.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





С
С
D
С
А
12 см
8 см
6см
А
D
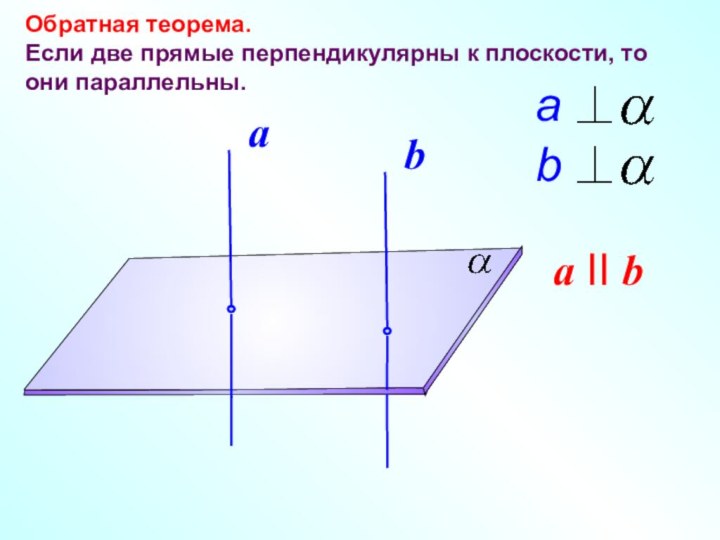
a
b
a
А
1
В
С
4
1
4
4
4
4
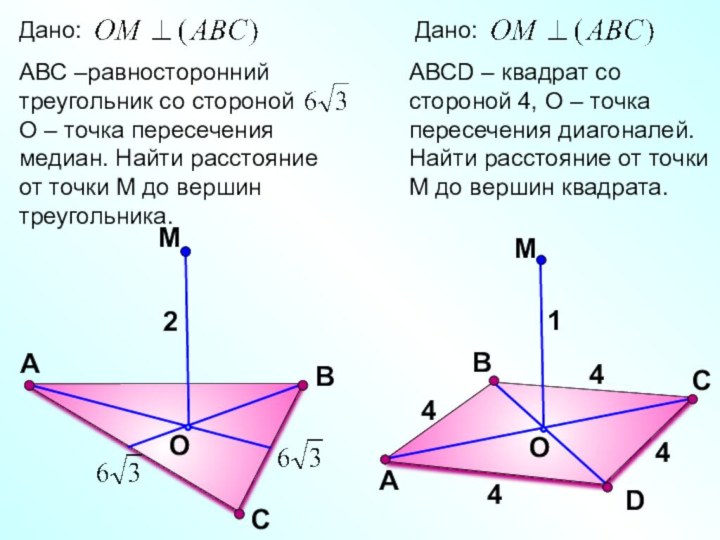
АВС –равносторонний треугольник со стороной
О – точка пересечения медиан. Найти расстояние от точки М до вершин треугольника.
Q
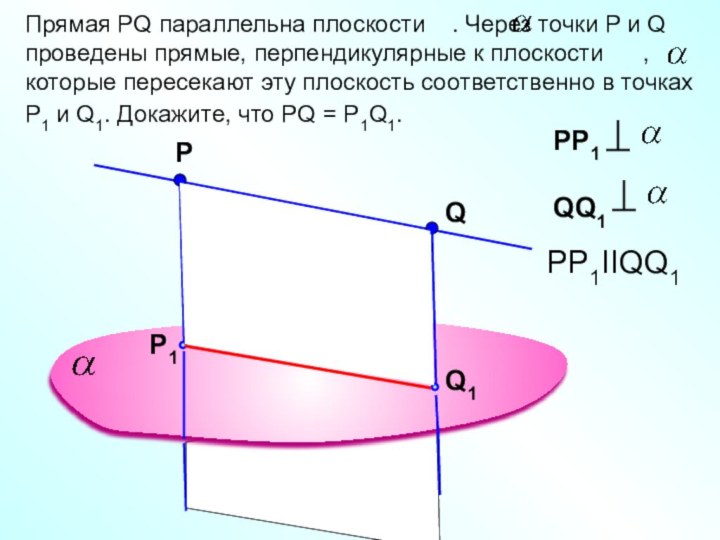
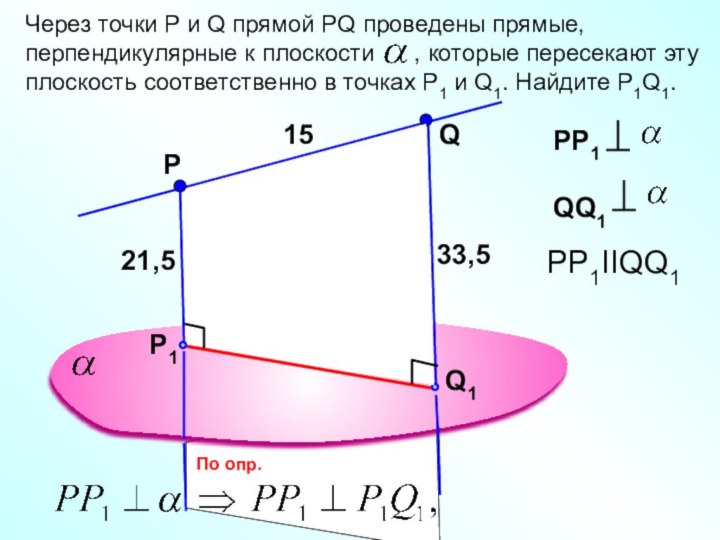
PP1IIQQ1