12
13
14
Тригонометрическая рулетка
15
16
17
финиш
23
33
1
3
18
0
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










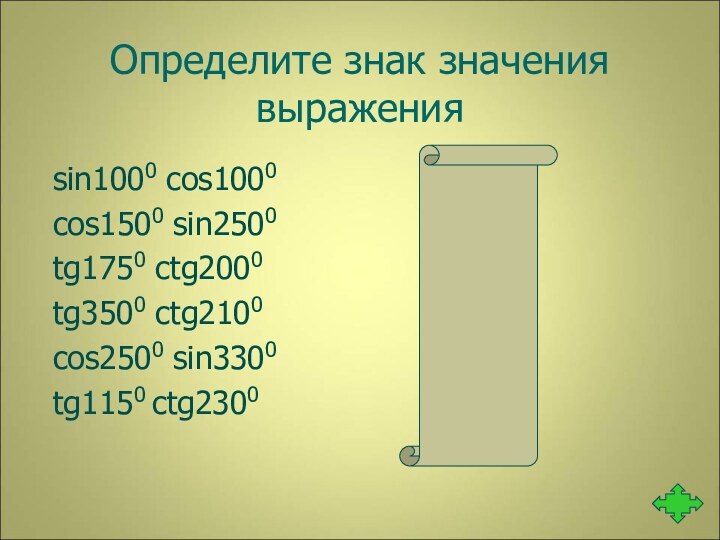










sin α < 0
cos α < 0
sin α < 0
cos α > 0
tg α < 0
tg α > 0
tg α > 0
tg α < 0
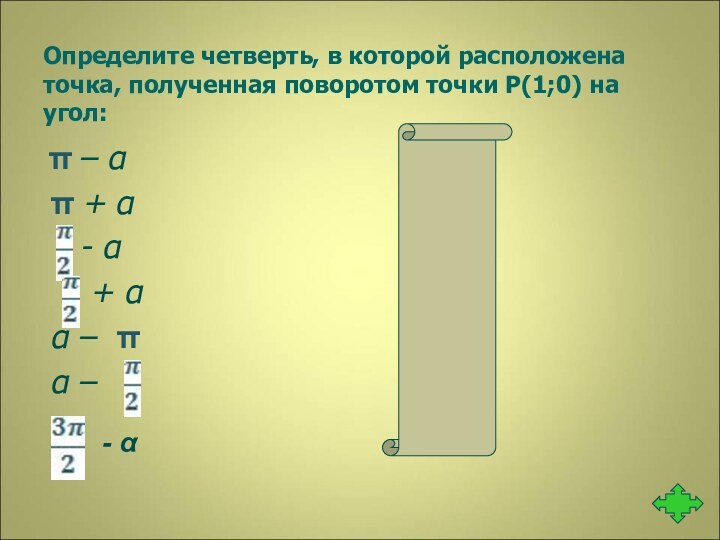
π
π
- α
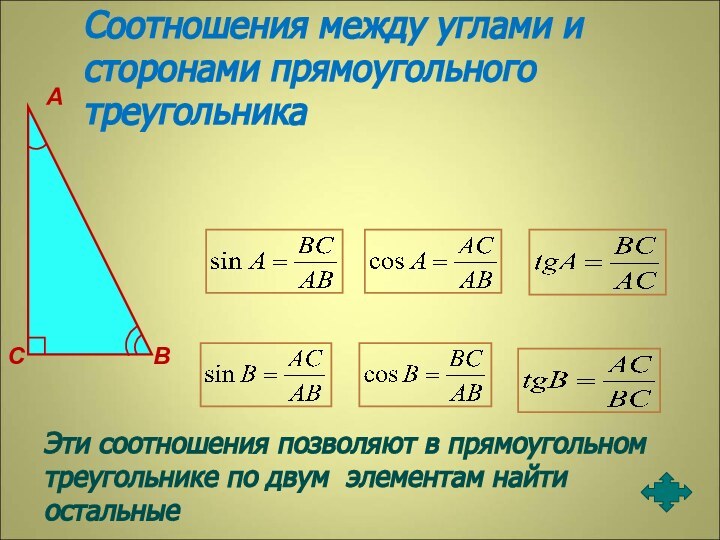
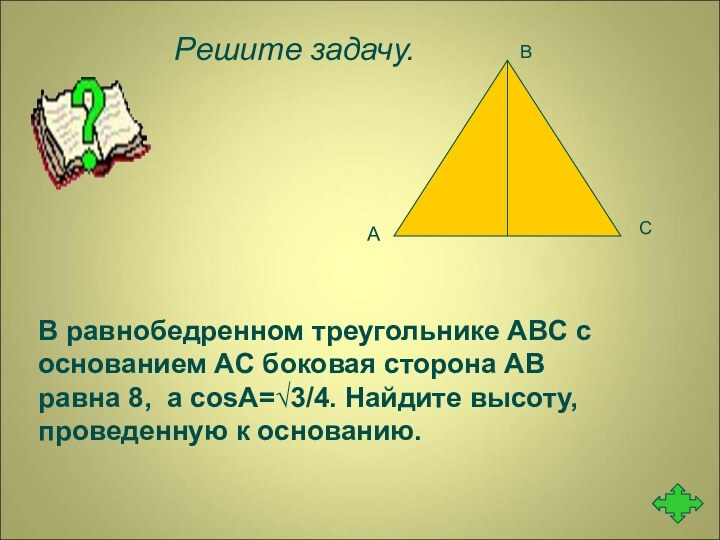
А
В
С