Слайд 2
ЦЕЛИ
1. Создать творческий проект по геометрии.
2. Обобщить, закрепить
и расширить знания, полученные в процессе изучение многогранников.
3. Формировать
навыки самостоятельной литературой и отбор необходимой информации.
4. Расширить кругозор математических знаний, выходя за приделы школьного курса геометрии.
5. Научиться моделировать правильные многогранники.
6.Формировать способность ставить перед собой задачи и учиться самостоятельно их решать.
7.Закрепить и улучшить навыки работы в программе Microsoft PowerPoint 2007
Слайд 3
Цели
Определение многогранника
Правильный многогранник
Пять типов
Происхождение названия
Тетраэдр
Октаэдр
Икосаэдр
Гексаэдр
Додекаэдр
Развертки
Платон
Платоновы тела
Олицетворение
СОДЕРЖАНИЕ
Тайна мировоззрения
Многогранники в
природе
Многогранники в архитектуре
Многогранники в животном мире
Используемая литература
Кресла
Вывод
Слайд 4
ОПРЕДЕЛЕНИЕ МНОГОГРАННИКА:
Часть пространства,
ограниченная совокупностью конечного числа плоских многоугольников, называется многогранной поверхностью
или многогранником.
Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами многогранника.
Слайд 5
Он выпуклый;
Все его грани равные правильные многоугольники;
В каждой
вершине сходится одно число РЕБЕР;
Все его двугранные углы равны
МНОГОГРАННИК
НАЗЫВАЕТСЯ ПРАВИЛЬНЫМ, ЕСЛИ:
Слайд 6
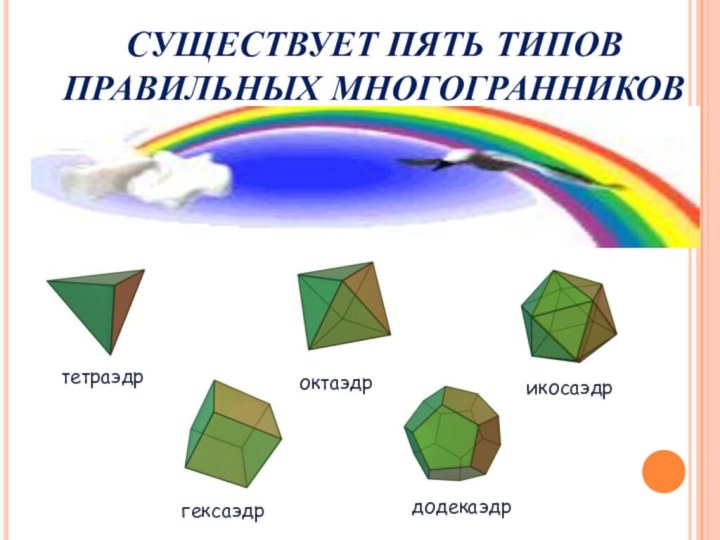
СУЩЕСТВУЕТ ПЯТЬ ТИПОВ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
тетраэдр
октаэдр
икосаэдр
гексаэдр
додекаэдр
Слайд 7
НАЗВАНИЕ КАЖДОГО МНОГОГРАННИКА ПРОИСХОДИТ ОТ ГРЕЧЕСКОГО НАЗВАНИЯ КОЛИЧЕСТВА
ЕГО ГРАНЕЙ И СЛОВА "ГРАНЬ".
«эдра» – грань
«тетра» - 4
«гекса»
- 6
«окта» - 8
«икоса» - 20
«додека» - 12
Слайд 8
ТЕТРАЭДР
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его
вершина является вершиной трех треугольников. У тетраэдра 4 грани,
6 ребер и 4 вершины
Слайд 9
ОКТАЭДР
Октаэдр составлен из восьми равносторонних треугольников . Каждая
его вершина является вершиной четырех треугольников. У октаэдра 8
граней, 12 ребер и 6 вершин.
Слайд 10
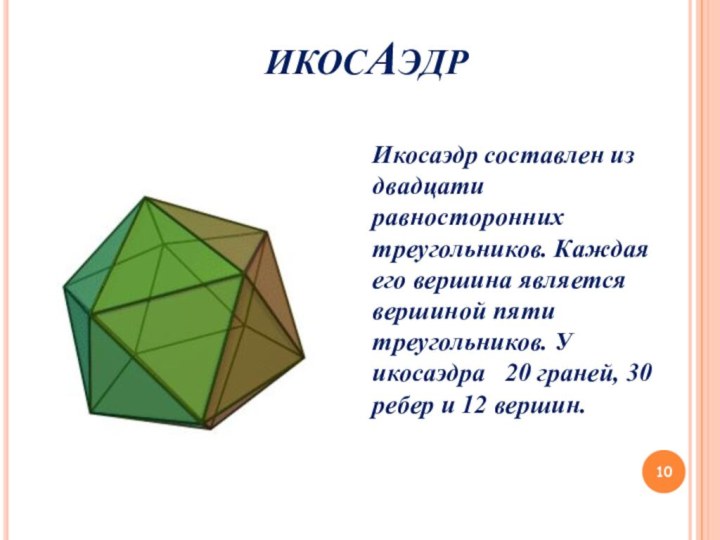
ИКОСАЭДР
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его
вершина является вершиной пяти треугольников. У икосаэдра 20
граней, 30 ребер и 12 вершин.
Слайд 11
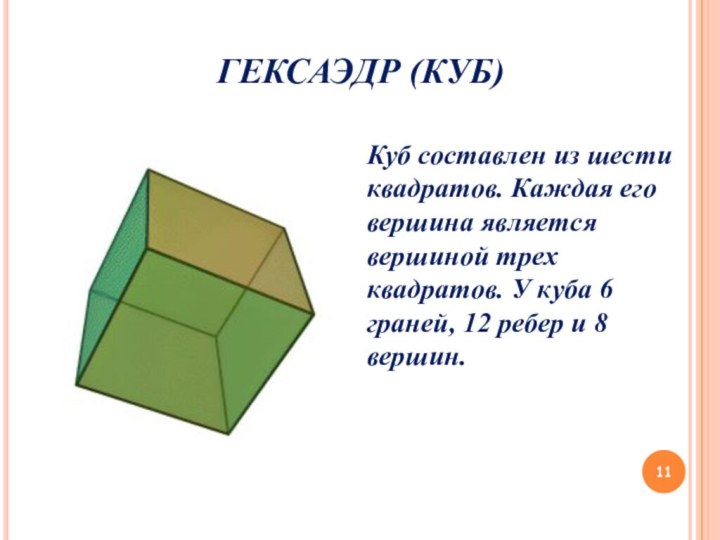
ГЕКСАЭДР (КУБ)
Куб составлен из шести квадратов. Каждая его
вершина является вершиной трех квадратов. У куба 6 граней,
12 ребер и 8 вершин.
Слайд 12
ДОДЕКАЭДР
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его
вершина является вершиной трех пятиугольников. У додекаэдра 30ребер,12
граней и 20 вершин.
Слайд 13
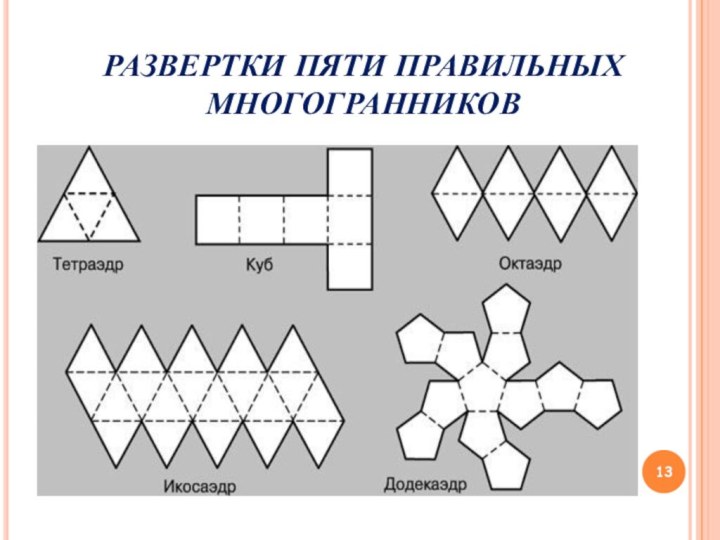
РАЗВЕРТКИ ПЯТИ ПРАВИЛЬНЫХ
МНОГОГРАННИКОВ
Слайд 14
В КАЖДОЙ ВЕРШИНЕ МНОГОГРАННИКА ДОЛЖНО СХОДИТЬСЯ СТОЛЬКО
ПРАВИЛЬНЫХ N – УГОЛЬНИКОВ, ЧТОБЫ СУММА ИХ УГЛОВ БЫЛА
МЕНЬШЕ 3600. Т.Е ДОЛЖНА ВЫПОЛНЯТЬСЯ ФОРМУЛА ΒK < 3600 ( Β-ГРАДУСНАЯ МЕРА УГЛА МНОГОУГОЛЬНИКА, ЯВЛЯЮЩЕГОСЯ ГРАНЬЮ МНОГОГРАННИКА, K – ЧИСЛО МНОГОУГОЛЬНИКОВ, СХОДЯЩИХСЯ В ОДНОЙ ВЕРШИНЕ МНОГОГРАННИКА.)
Слайд 15
Древнегреческий ученый и
философ ПЛАТОН
Ни
одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Со слов Бертрана Рассела: "Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”. Название "правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона.
Слайд 17
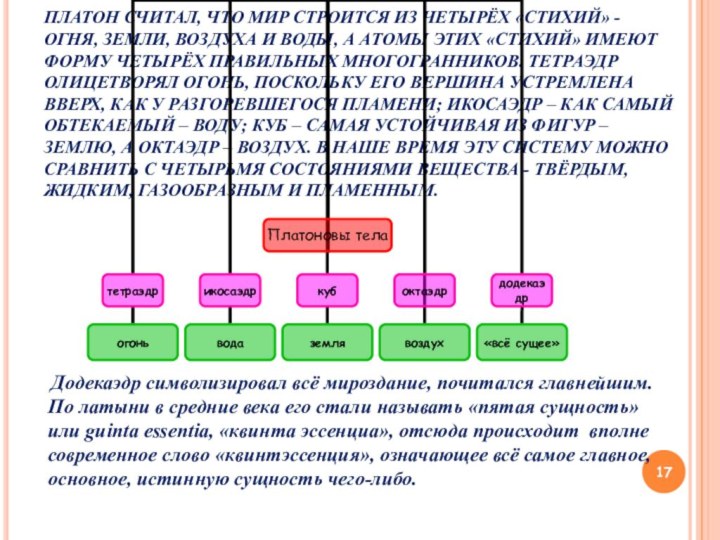
ПЛАТОН СЧИТАЛ, ЧТО МИР СТРОИТСЯ ИЗ ЧЕТЫРЁХ «СТИХИЙ»
- ОГНЯ, ЗЕМЛИ, ВОЗДУХА И ВОДЫ, А АТОМЫ ЭТИХ
«СТИХИЙ» ИМЕЮТ ФОРМУ ЧЕТЫРЁХ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ. ТЕТРАЭДР ОЛИЦЕТВОРЯЛ ОГОНЬ, ПОСКОЛЬКУ ЕГО ВЕРШИНА УСТРЕМЛЕНА ВВЕРХ, КАК У РАЗГОРЕВШЕГОСЯ ПЛАМЕНИ; ИКОСАЭДР – КАК САМЫЙ ОБТЕКАЕМЫЙ – ВОДУ; КУБ – САМАЯ УСТОЙЧИВАЯ ИЗ ФИГУР – ЗЕМЛЮ, А ОКТАЭДР – ВОЗДУХ. В НАШЕ ВРЕМЯ ЭТУ СИСТЕМУ МОЖНО СРАВНИТЬ С ЧЕТЫРЬМЯ СОСТОЯНИЯМИ ВЕЩЕСТВА - ТВЁРДЫМ, ЖИДКИМ, ГАЗООБРАЗНЫМ И ПЛАМЕННЫМ.
Додекаэдр символизировал всё мироздание, почитался главнейшим. По латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 18
ТАЙНА МИРОВОЗЗРЕНИЯ
По теории Платона вокруг тетраэдра описана сфера
Юпитера, вписанная в куб. Вокруг сферы Меркурия, ближайшей к
Солнцу планеты, описан октаэдр. Вокруг куба описана сфера Сатурна. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр.
Слайд 20
Правильные многогранники встречаются в живой природе. Например, скелет
одноклеточного организма феодарии по форме напоминает икосаэдр.
Чем же вызвана
такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной тощи.
Феодария
Слайд 21
Поваренная соль состоит из кристаллов в форме куба.
Минерал
куприт образует кристаллы в форме октаэдров.
Слайд 22
Кристаллы алмаза представляют собой гигантские полимерные молекулы и
обычно имеют форму октаэдров
Молекулы воды имеют форму тетраэдра
Слайд 26
ЕГИПЕТСКИЕ ПИРАМИДЫ
Они словно вырастают из песков пустыни -
колоссальные, величественные, подавляющие человека необычайными размерами и строгостью очертаний.
Стоя у подножия пирамиды, трудно себе представить, что эти огромные каменные горы созданы руками людей. А между тем они были действительно сложены из отдельных каменных глыб, как в наше время дети складывают пирамиды из кубиков.
Слайд 27
Египетские пирамиды хранят в себе огромное количество тайн
и загадок. Однако загадки внешних характеристик пирамид - это
еще цветочки. Поразительно также и то, что происходит внутри. До сих пор не известно точно, почему внутри пирамиды, ориентированной по сторонам света, проявляется эффект мумификации любой органики. Тела мелких животных, умерших в пирамиде, даже без бальзамирования мумифицируются и сохраняются очень длительное время. Важно заметить, что эффект мумификации наиболее сильно наблюдается в центре пирамиды, примерно на высоте 1/3 ее высоты. Примерно на этой высоте находились захоронения фараонов. Кроме того, в пирамиде тупые лезвия бритвы, положенные с сохранением ориентировки по сторонам света, в короткое время затачиваются.
ЕГИПЕТСКИЕ ПИРАМИДЫ
Слайд 28
ВИСЯЧИЕ САДЫ СЕМИРАМИДЫ
Дворец Навуходоносора был построен для его
жены Семирамиды на обширной кирпичной площадке, высоко поднимавшейся над
окружающей местностью. Пять дворов следовали один за другим с востока на запад, во дворы выходили двери многочисленных комнат. Фасад украшали стройные желтые колонны с голубыми завитками. Окон не было, и свет проникал через три широкие двери.
Слайд 29
МНОГОГРАННЫЕ БАШНИ СМОЛЕНСКОЙ КРЕПОСТИ
Слайд 31
СПАССКАЯ БАШНЯ КРЕМЛЯ
Четырехъярусная Спасская башня с надвратной церковью
Спаса Нерукотворного — главный въезд в Казанский кремль —
расположена в южном прясле крепостной стены. Возведена в XVI веке псковскими зодчими Иваном Ширяем и Постником Яковлевым по прозванию «Барма». Башня неоднократно перестраивалась, во все века ей как главной кремлевской башне уделяли особое внимание. Четыре яруса башни представляют из себя куб, многогранники и пирамиду.
Слайд 32
МЕЧЕТЬ
КУЛ-ШАРИФ
Одна из главных мусульманских мечетей республики Татарстан
и Казани. Расположена на территории Казанского кремля. Архитектура
этой мечети представляет собой сочетание различных многогранников.
Слайд 35
«ТАЙНАЯ ВЕЧЕРЯ» С. ДАЛИ
Сальвадор Дали на картине «Тайная
вечеря» изобразил И. Христа со своими учениками на фоне
огромного прозрачного додекаэдра. Учеными достаточно хорошо изучены правильные выпуклые многогранники, но сам ли человек их придумал? Скорее всего – нет, он «подсмотрел» их у природы.
Слайд 36
В эпоху Возрождения большой интерес к формам правильных
многогранников проявили скульпторы. архитекторы, художники. Леонардо да Винчи (1452
-1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли ''О божественной пропорции.''
Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.
“Меланхолия”
Слайд 38
Металлическое кресло Hedronics в виде многогранника
Слайд 39
Вывод
Во время работы над проектом мы узнали много
нового и интересного.
Благодаря правильным многогранникам открываются не только удивительные
свойства геометрических фигур, но и пути познания природной гармонии.
Мы создали творческий проект по геометрии.
Обобщили, закрепили и расширили знания, полученные в процессе изучение многогранников.
Сформировали навыки самостоятельной литературой и отбора необходимой информации.
Смоделировали правильные многогранники.
Расширили кругозор математических знаний, выходя за приделы школьного курса геометрии.
Научились моделировать правильные многогранники.
Закрепили и улучшили навыки работы в программе Microsoft PowerPoint 2007