не лежащей на данной прямой, можно провести перпендикуляр к
этой прямой, ................................................
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


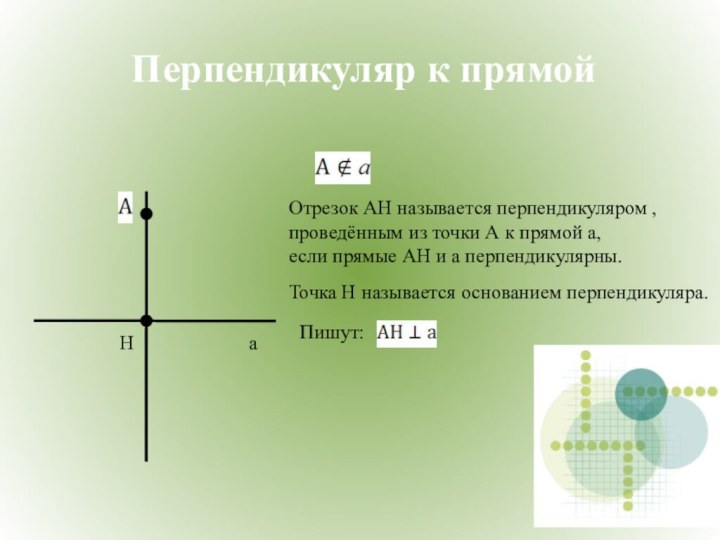



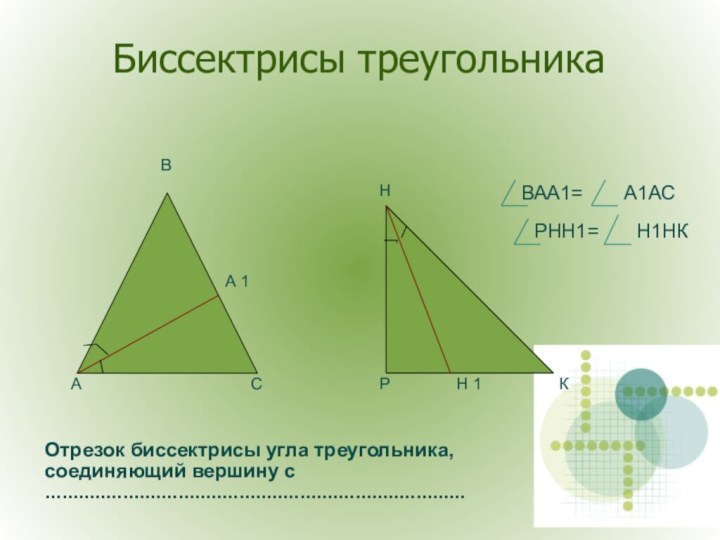
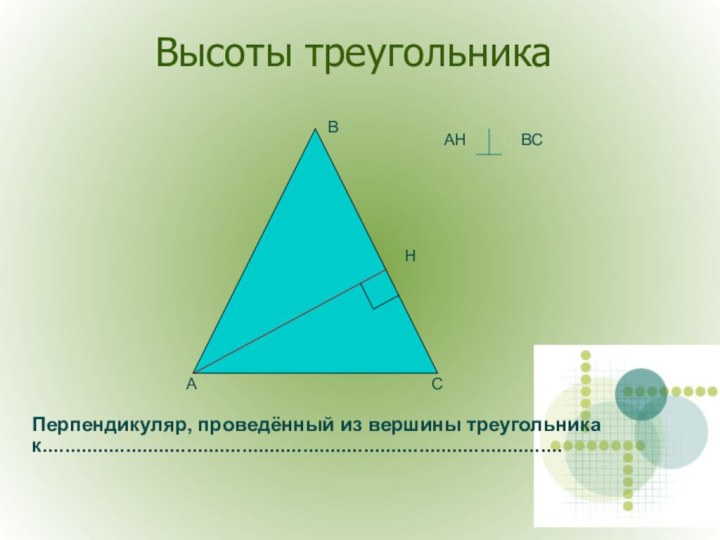

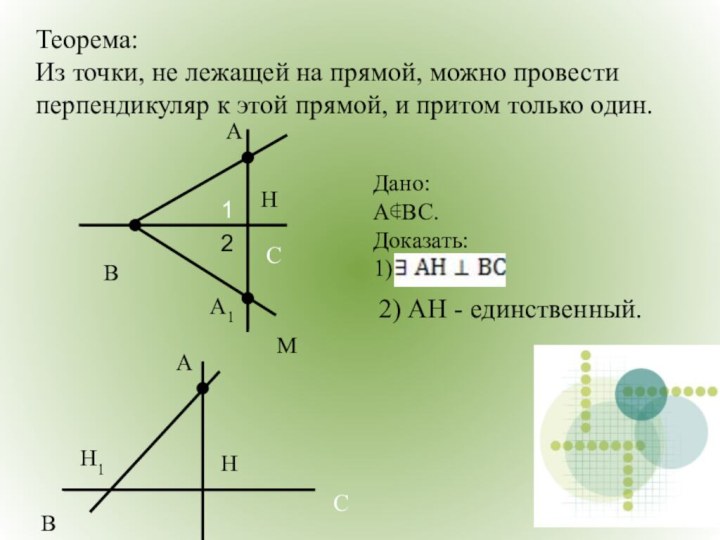



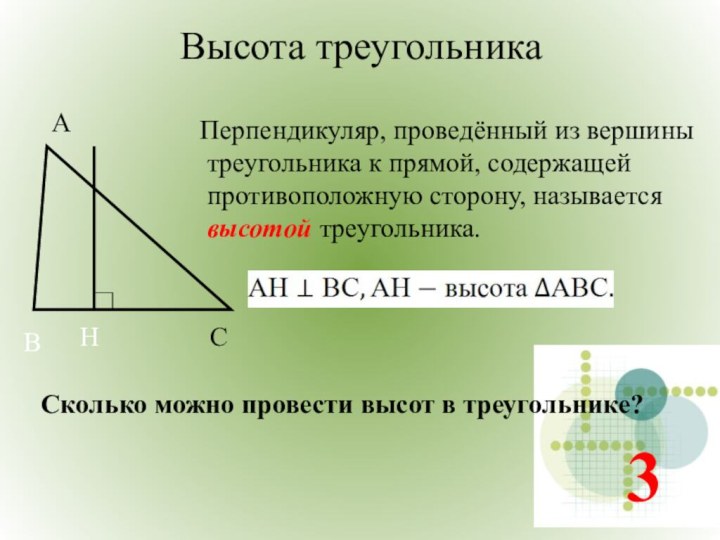


Точка Н называется основанием перпендикуляра.
Пишут:
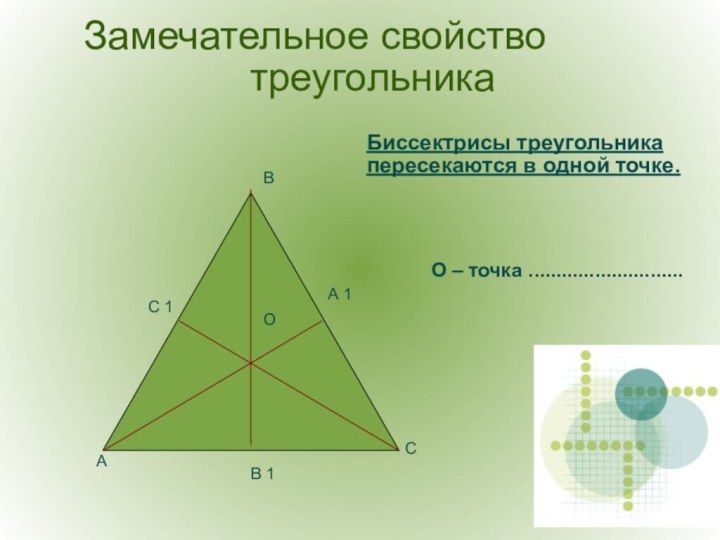
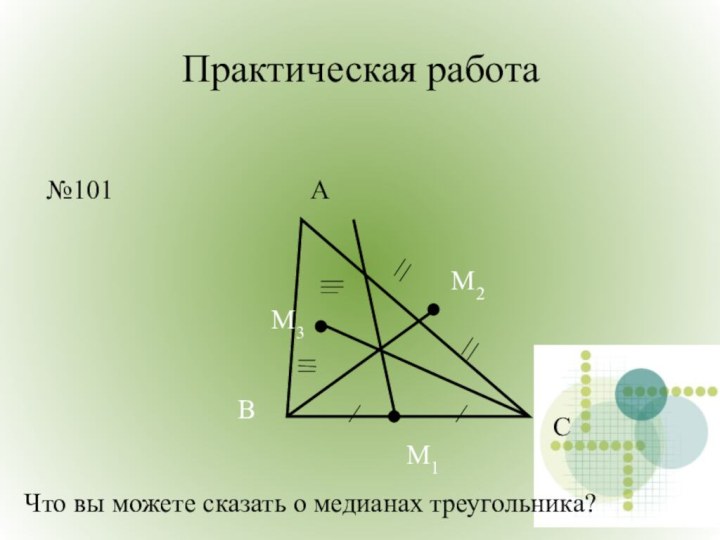
Медианы треугольника пересекаются в одной точке.
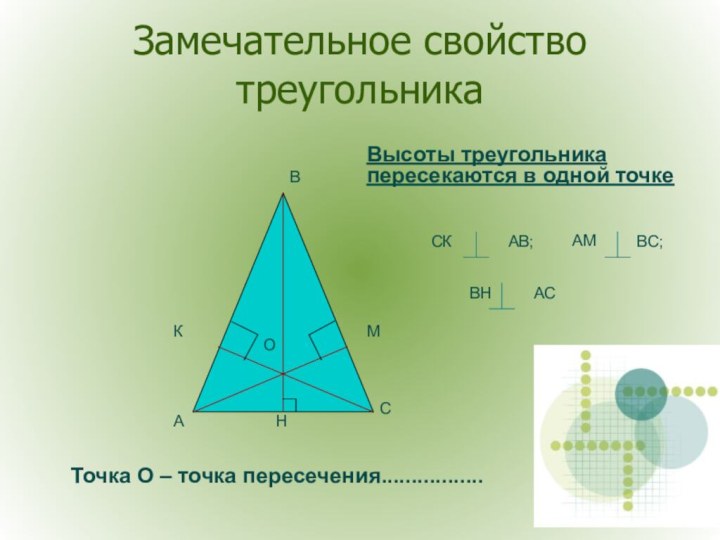
О – точка ............................
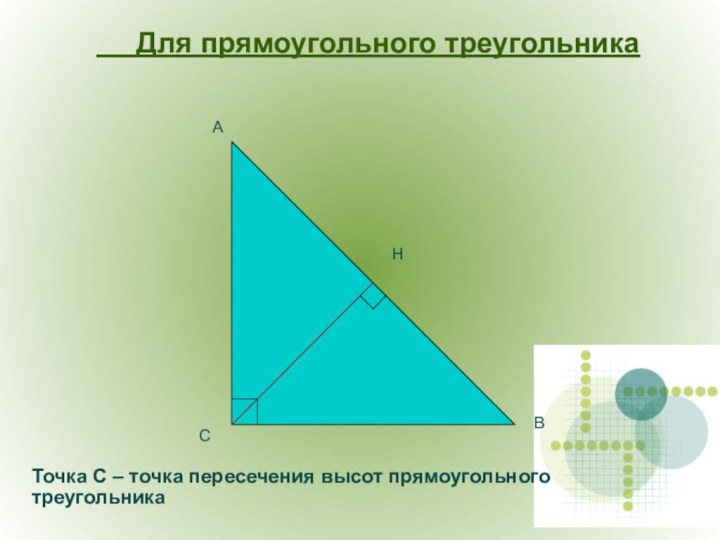
О – точка ............................
2) АН - единственный.
В
С
А
М
А1
Н
1
2
В
С
А
Н
Н1
3
3
3