и высшей красотой - красотой отточенной и строгой, возвышенно
чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»Бертран Рассел
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















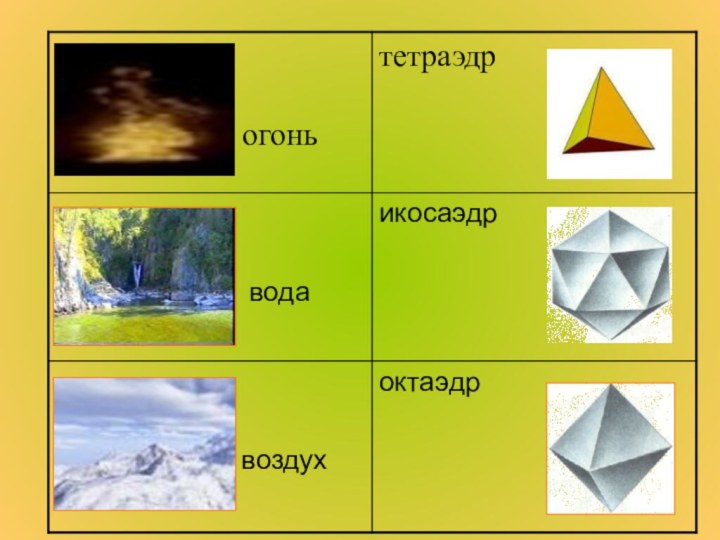






МНОГОГРАННИК
В книге немецкого биолога Э. Геккеля "Красота форм в природе"
можно прочитать такие строки:
«Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»:
Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.
Это свойство помогает морскому организму преодолевать давление толщи воды.
Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников:
Историческая справка
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком
пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.