изучает свойства фигур на плоскости.
Стереометрия изучает свойства фигур
в пространстве.Предмет стереометрии. Аксиомы стереометрии
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



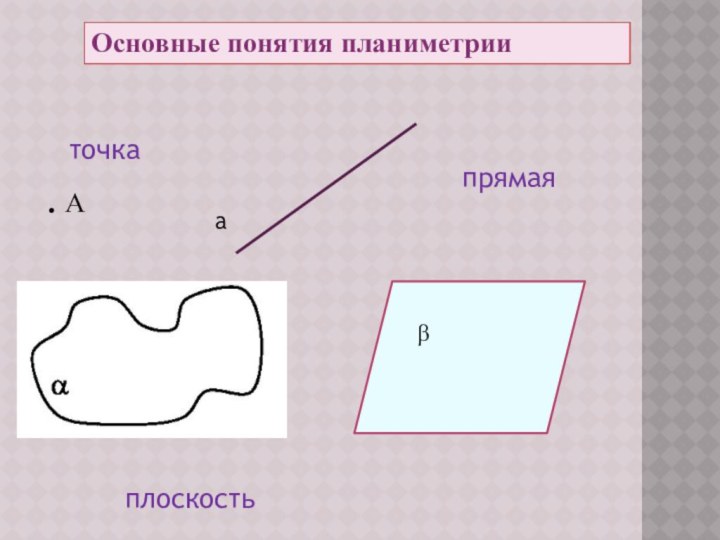
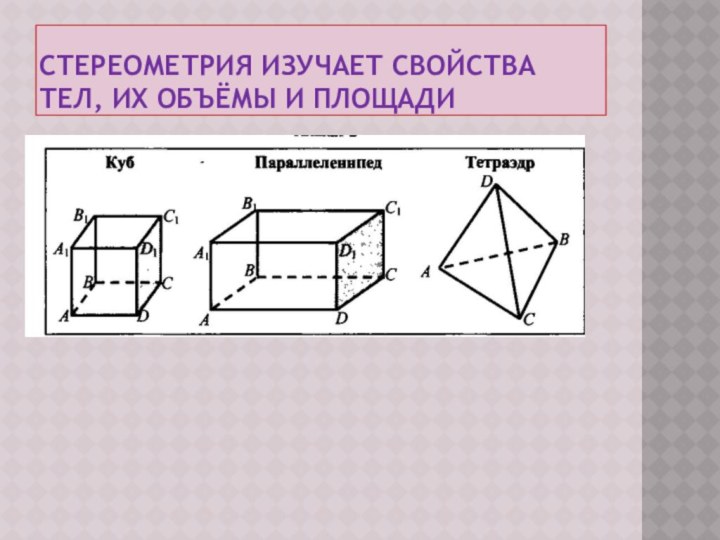










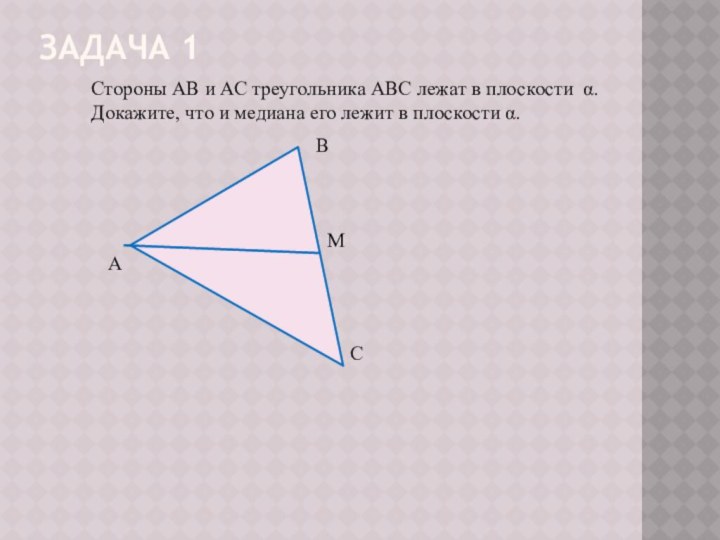

Предмет стереометрии. Аксиомы стереометрии
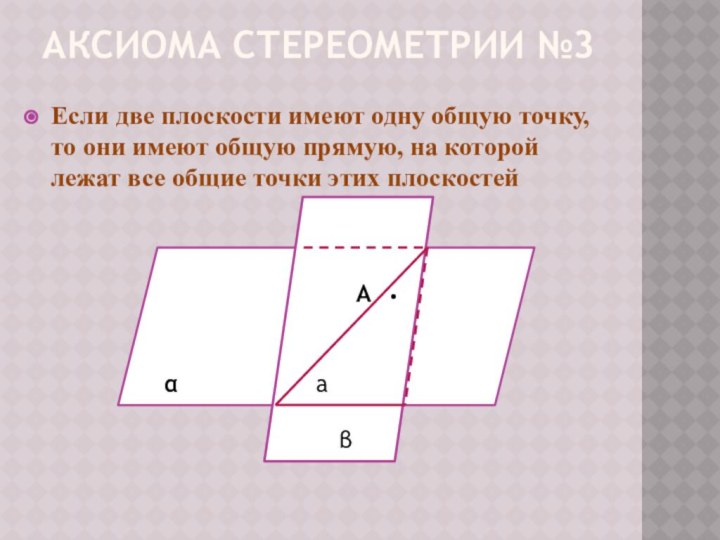
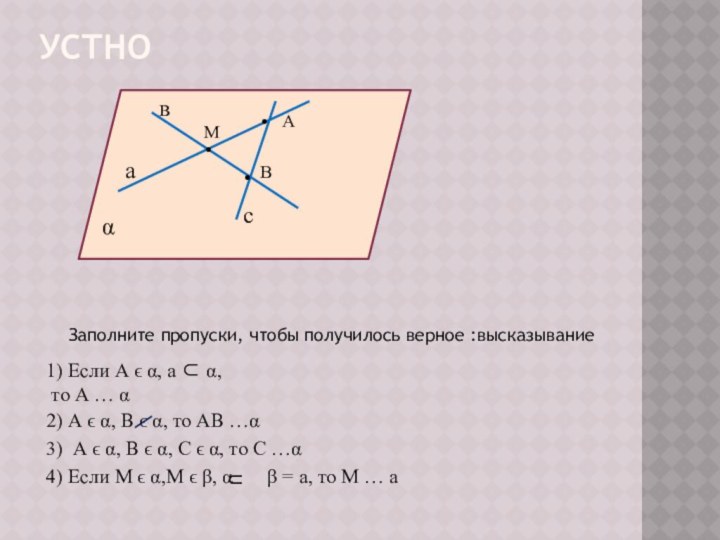
• В
•
С
α
α
β
а
А •
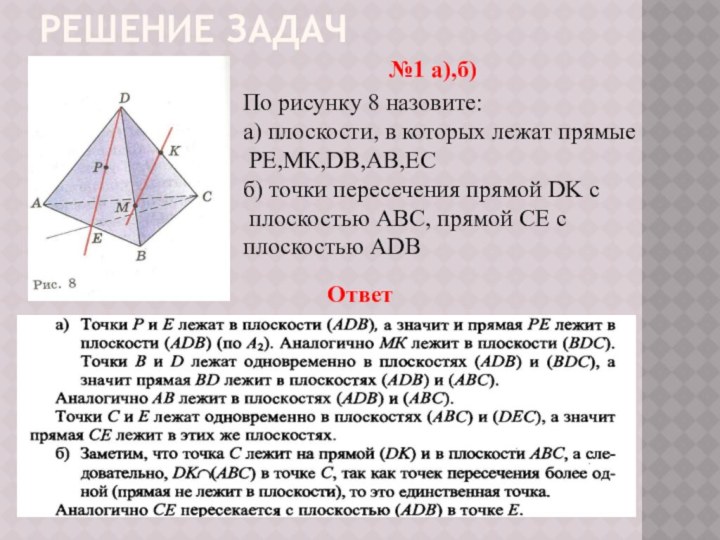
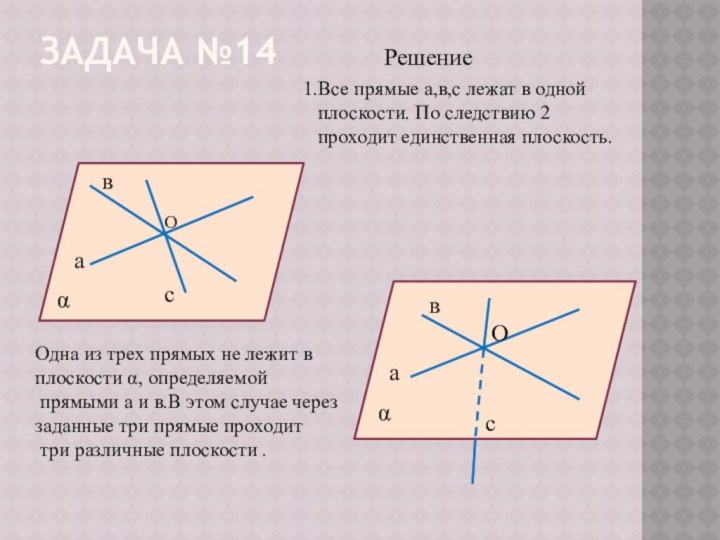
№1 а),б)
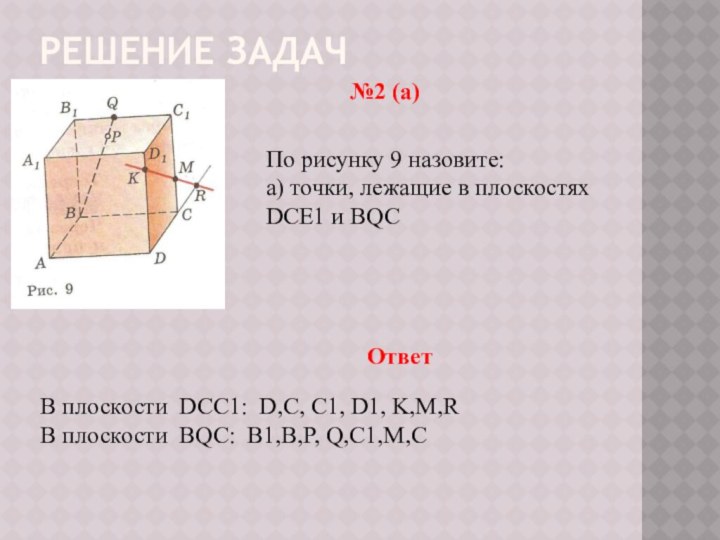
Ответ
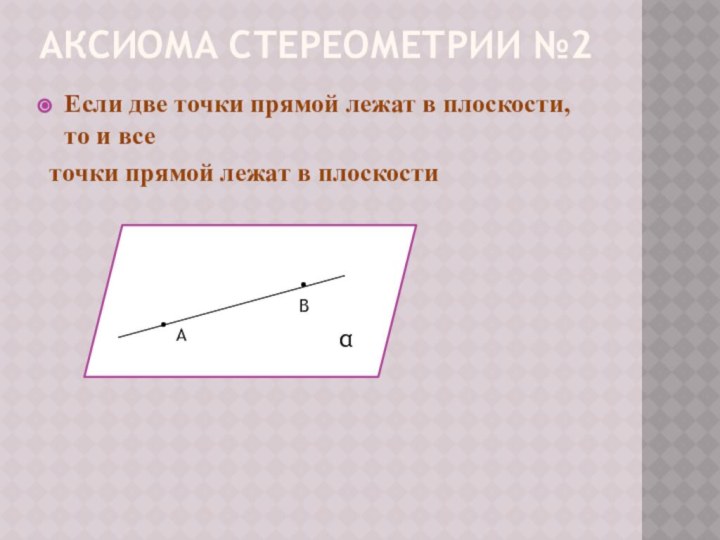
Если две плоскости имеют одну общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей
В•
С•
D•
α
A•
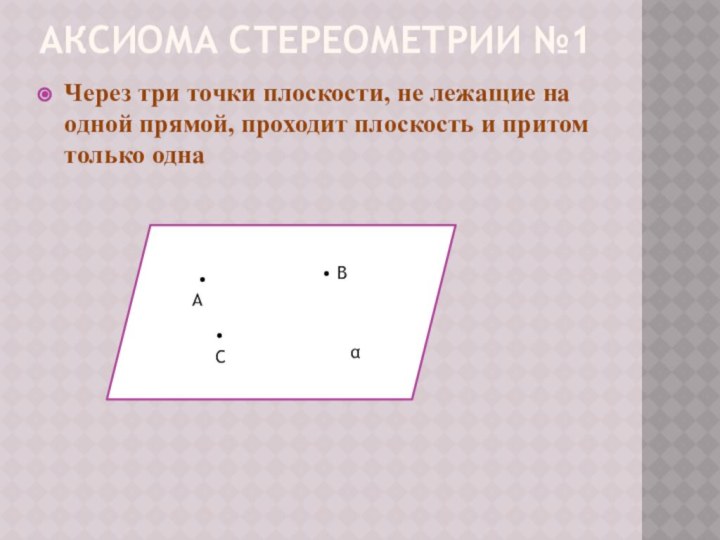
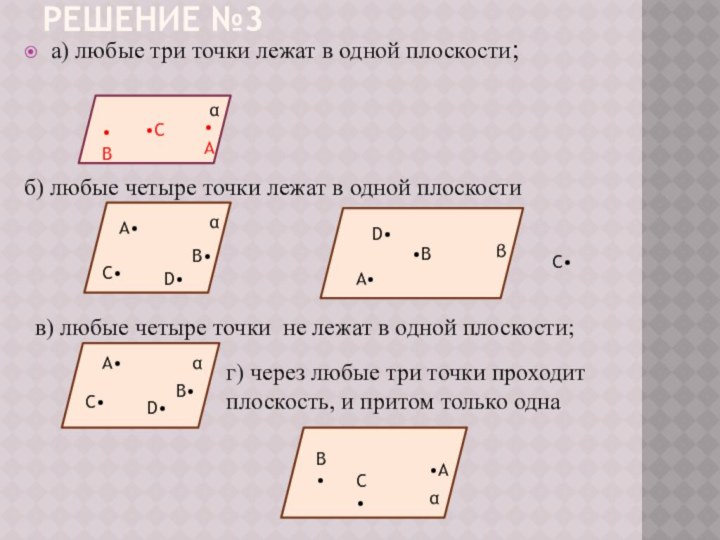
г) через любые три точки проходит плоскость, и притом только одна
B•
•A
C•
α
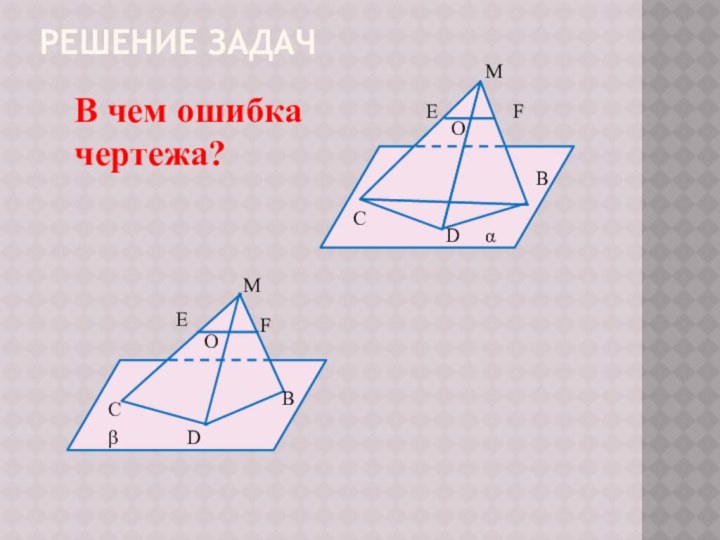
Доказательство
1. Рассмотрим прямую а не лежащую на ней точку М.отметим на
прямой а две точки P и Q. Точки P, Q, М не лежат на одной прямой,
поэтому согласно аксиоме А1 через эти точки проходит некоторая
плоскость α. Так как 2 точки прямой а ( Р и Q)лежат в плоскости α,
то по аксиомеА2 плоскость αпроходит через прямую а.
2. Единственность плоскости, проходящей через прямую а и точку М, следует из того, что любая плоскость, проходящая через прямую а и точку М, проходит через точки Р, М и Q. Следовательно эта плоскость совпадает с плоскостью α, так как по аксиоме А1 через точки Р, М и Q проходи только одна плоскость.
U
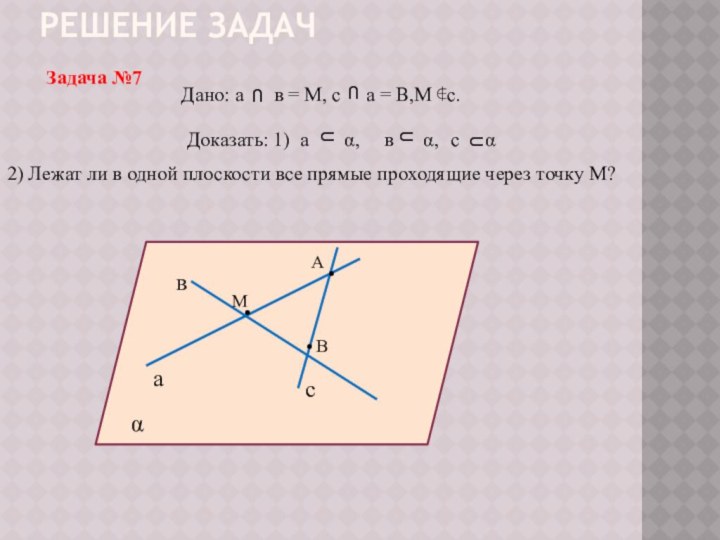
Доказать: а и в ϵ α
Доказательство:
Дополнительное построение ( точка N).
Плоскость α проходит через прямую в и точку N.
Аксиома А2. ( две точки прямой а лежат
в плоскости α).
4. Вывод.
5. Единственность ( Любая плоскость, проходящая
через прямые а и в, проходит через точку N).
6. Плоскости совпадают.
2) А ϵ α, В ϵ α, то АВ …α
3) А ϵ α, В ϵ α, С ϵ α, то С …α
4) Если М ϵ α,М ϵ β, α β = а, то М … а
U
а
в
с
•
•
•
M
А
В
α
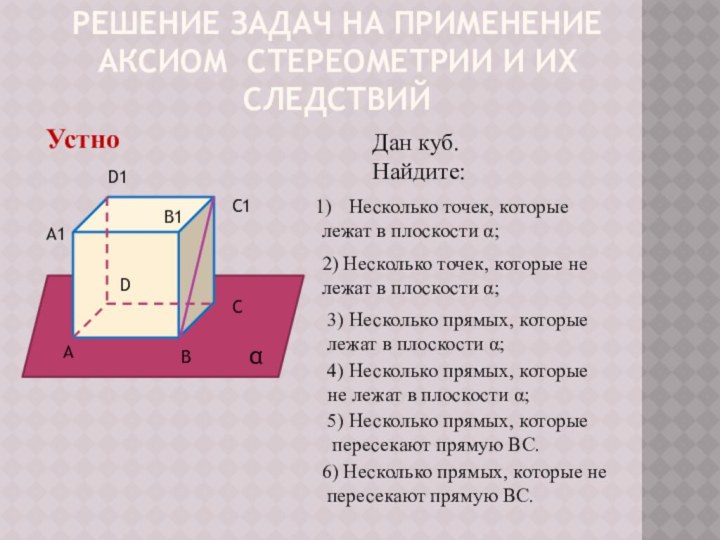
3) Несколько прямых, которые
лежат в плоскости α;
4) Несколько прямых, которые
не лежат в плоскости α;
5) Несколько прямых, которые
пересекают прямую ВС.
6) Несколько прямых, которые не
пересекают прямую ВС.
D
А
В
С
А1
С1
В1
D1
α
Доказать: (АВ, ВС, АС) (АВС)
U
Доказательство:
1. (А,В,С) ϵ α, так как две точки принадлежат одной прямой, то по А2 (А, В, С) ϵ (АВС)
2. (А,В,С) ϵ α. Через А, В, С по аксиоме А1 проходит единственная плоскость. Две точки каждого из отрезков АВ, ВС, АС лежат в плоскости, следовательно по аксиоме А2 прямые АВ, ВС, АС , а значит и отрезки
АВ, ВС, АС лежат в плоскости α, ч.т.д.
α
А
В
С
α
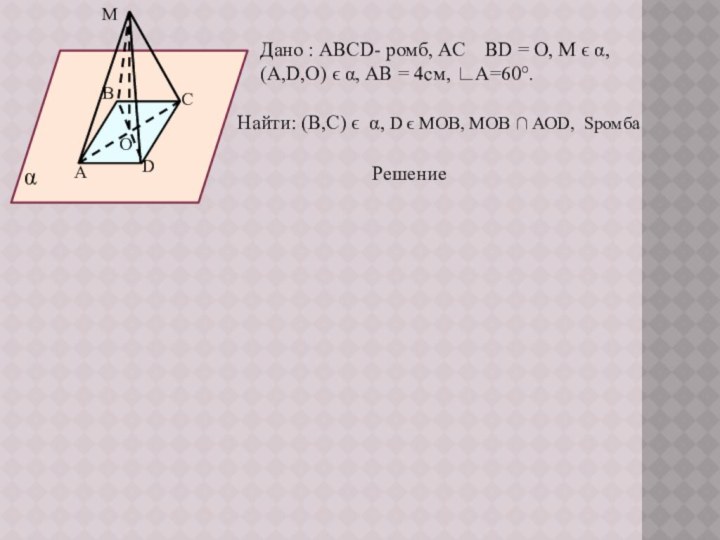
1) Лежат ли точки В и С в плоскости α?
2)Лежит ли в плоскости МОВ точка D?
3) Назовите линию пересечения плоскостей МОВ и АОD.
4) Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60°
Найти: (В,С) ϵ α, D ϵ МОВ, МОВ ∩ АОD, Sромба
Решение
М
С
D
А
В
О
α
Найти: (В,С) ϵ α, D ϵ МОВ, МОВ ∩ АОD, Sромба
Решение
D ϵ α, О ϵ α, по А2 DO ⊂ α, так как В ϵ DO, то В ϵ α. Аналогично
А ϵ α, О ϵ α, то по А2 АО ϵ α, так как С ϵ АО, то С ϵ α.
2) ОВ ϵ МОВ, D ϵ ОВ, то D ϵ МОВ.
3) О ϵ МОВ, О ϵ АОD.
В ϵ МОВ,В ϵ АОD , следовательно, МОВ АОD=ВО, но так как
ВО часть ВD, то АОВ АОD=ВD
∩
U
Если 2 плоскости имеют общие точки, то они пересекаются по
прямой, проходящей через эти точки
4) Sромба=4· 4 ·sin60°=8 √3 (см²)
М
С
D
А
В
О
α
U
α,
в α,
U
с α
U
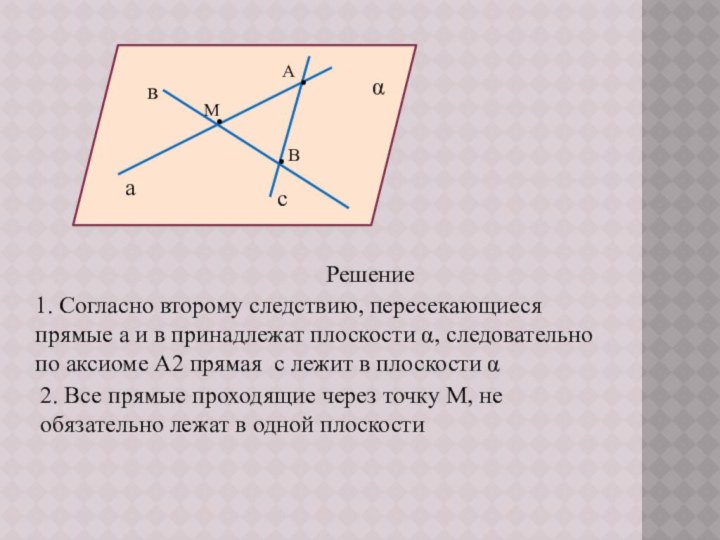
2) Лежат ли в одной плоскости все прямые проходящие через точку М?
в
а
с
•
•
•
М
А
В
α
2. Все прямые проходящие через точку М, не обязательно лежат в одной плоскости
в
а
с
•
•
М
А
В
•
α
•
А
А1
В
М
В1
С1
С
N
D
K
D1
O
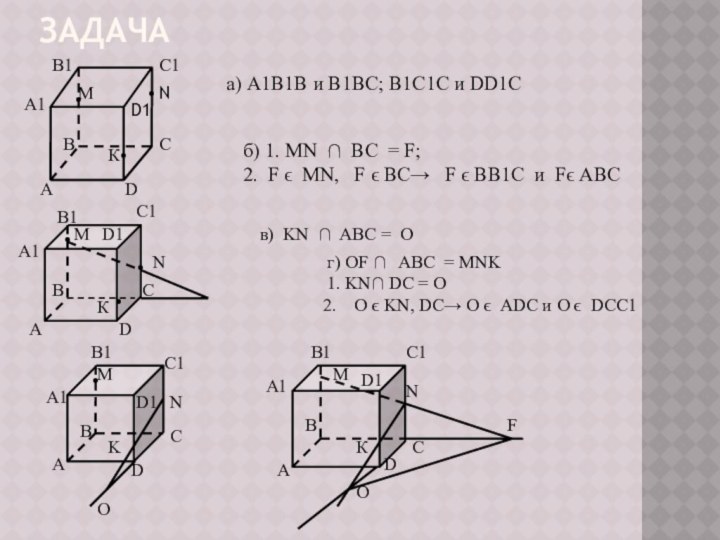
в) KN ∩ ABC = O
А
О
В
В1
А1
М
С1
С
К
N
F
D1
D
г) OF ∩ ABC = MNK
1. KN∩ DC = O
O ϵ KN, DC→ O ϵ ADC и
O ϵ DCC1
α
А
В
С
D
О
α
А
В
С
D
О
.
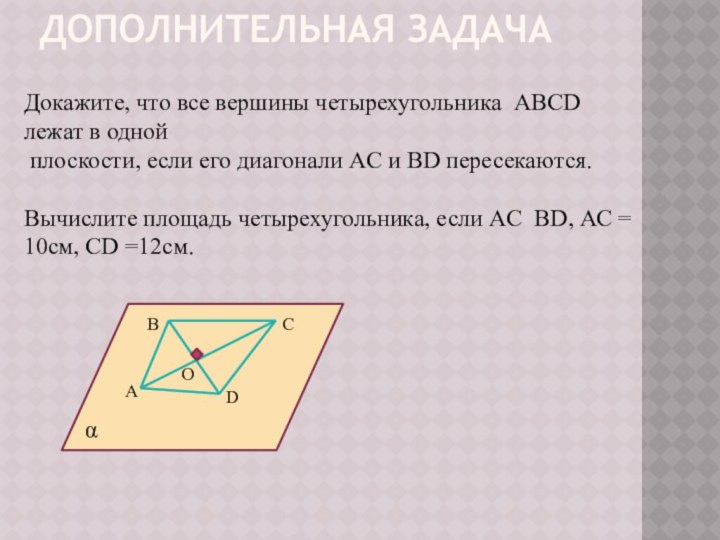
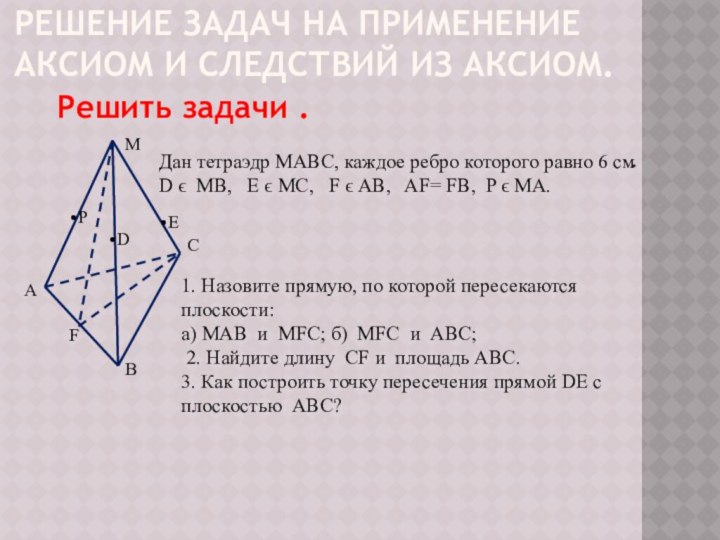
1. Назовите прямую, по которой пересекаются плоскости:
а) MAB и MFC; б) MFC и ABC;
2. Найдите длину CF и площадь АВС.
3. Как построить точку пересечения прямой DE с плоскостью ABC?
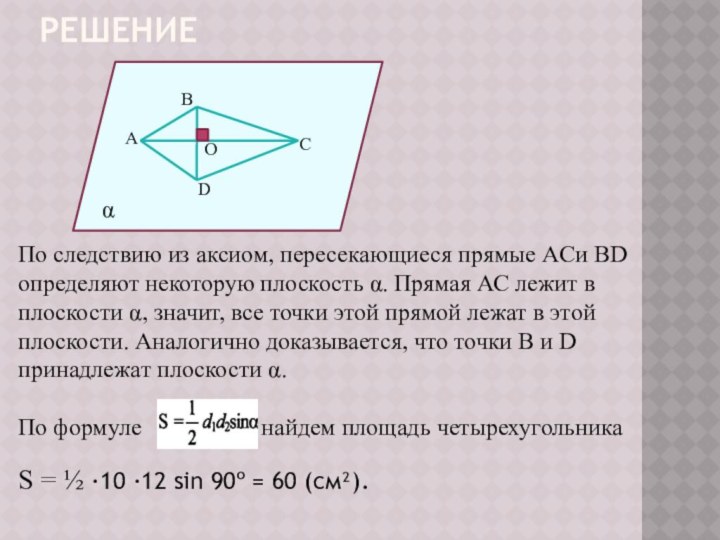
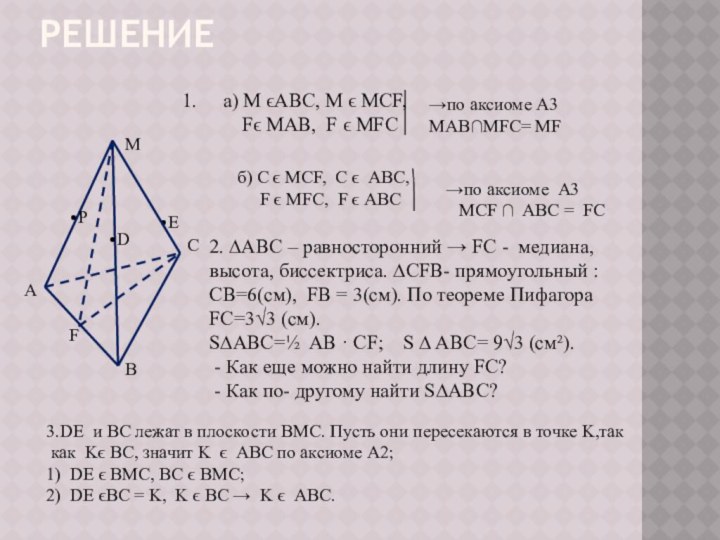
б) C ϵ MCF, C ϵ ABC,
F ϵ MFC, F ϵ ABC
→по аксиоме А3
MCF ∩ ABC = FC
2. ∆АВС – равносторонний → FC - медиана, высота, биссектриса. ∆CFB- прямоугольный : CB=6(см), FB = 3(см). По теореме Пифагора FC=3√3 (см).
S∆ABC=½ AB · CF; S ∆ ABC= 9√3 (см²).
- Как еще можно найти длину FC?
- Как по- другому найти S∆ABC?
3.DE и BC лежат в плоскости BMC. Пусть они пересекаются в точке K,так
как Kϵ BC, значит K ϵ ABC по аксиоме A2;
1) DE ϵ BMC, BC ϵ BMC;
2) DE ϵBC = K, K ϵ BC → K ϵ ABC.
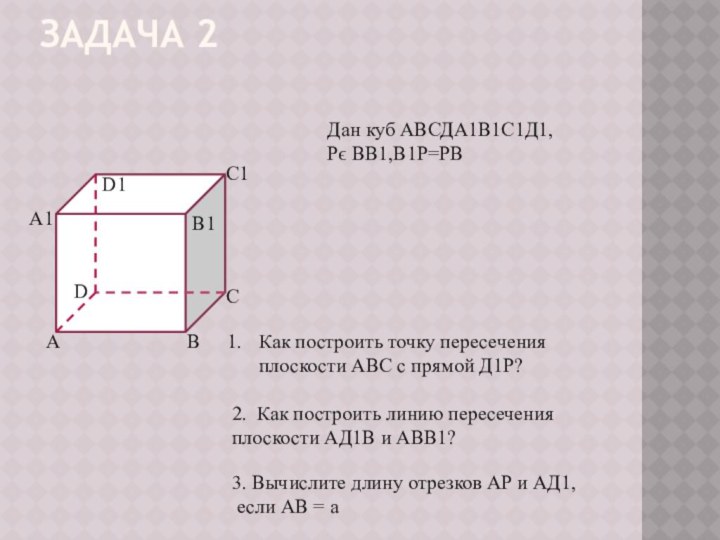
3. Вычислите длину отрезков АР и АД1,
если АВ = а
А
В
С
D
A1
B1
C1
D1
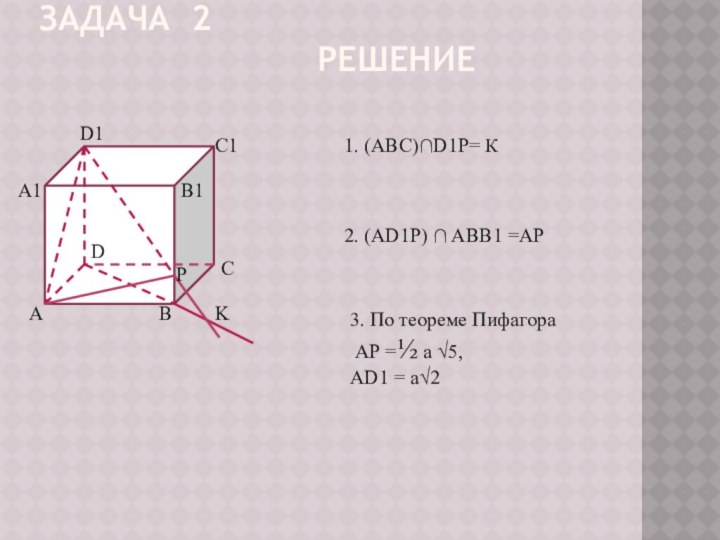
2. (AD1P) ∩ АВВ1 =АР
3. По теореме Пифагора
АР =½ а √5,
АD1 = a√2
α
β
а
В
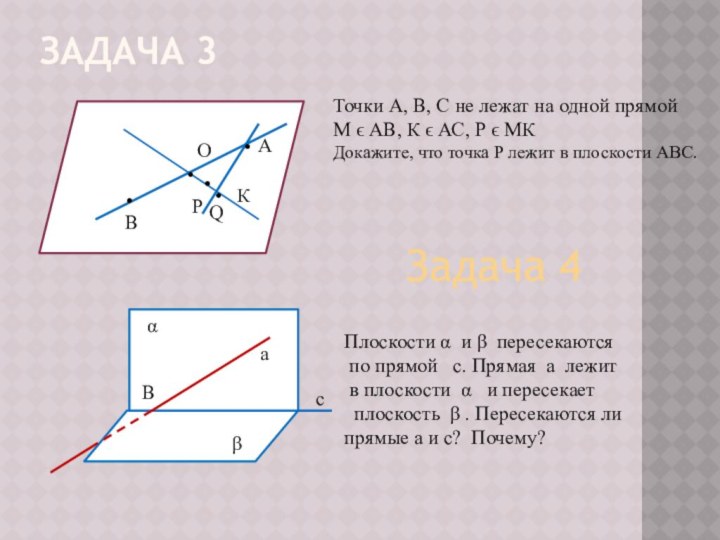
Задача 4
Плоскости α и β пересекаются
по прямой с. Прямая а лежит
в плоскости α и пересекает
плоскость β . Пересекаются ли
прямые а и с? Почему?
с
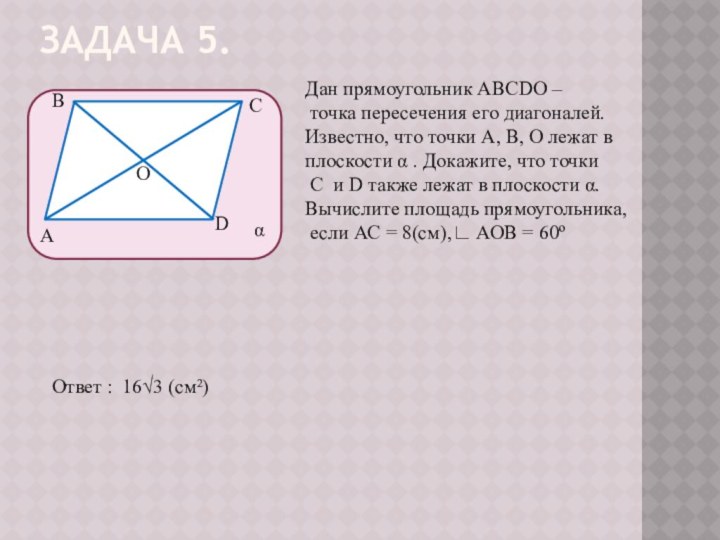
Ответ : 16√3 (см²)
А
В
М
С