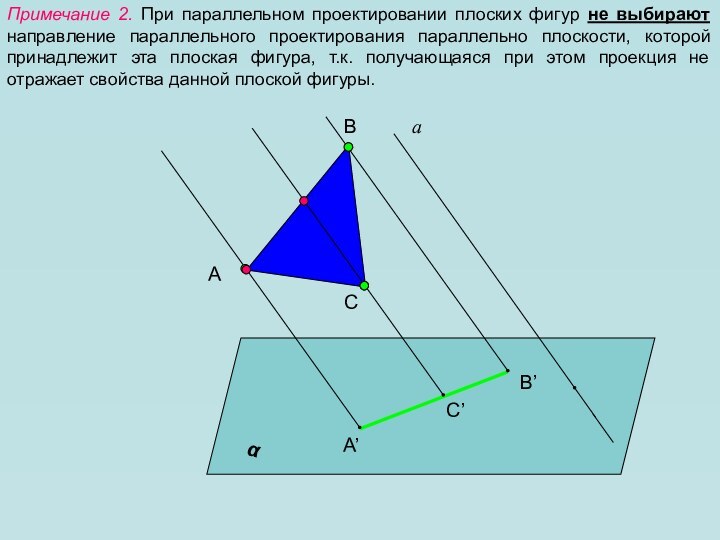
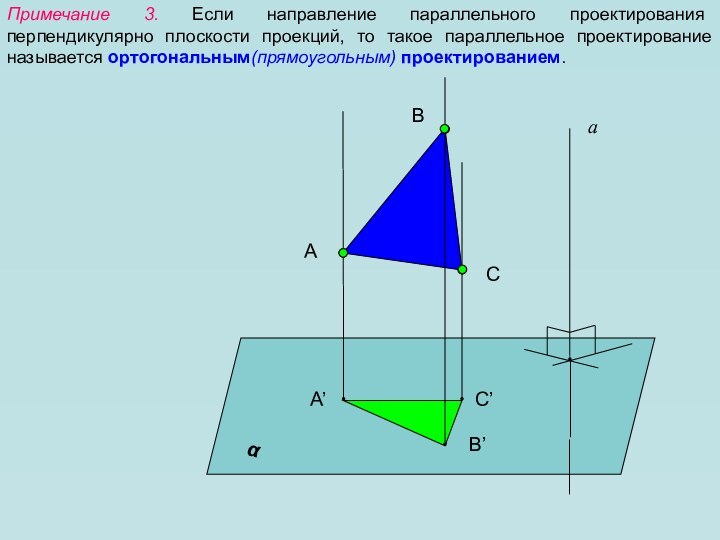
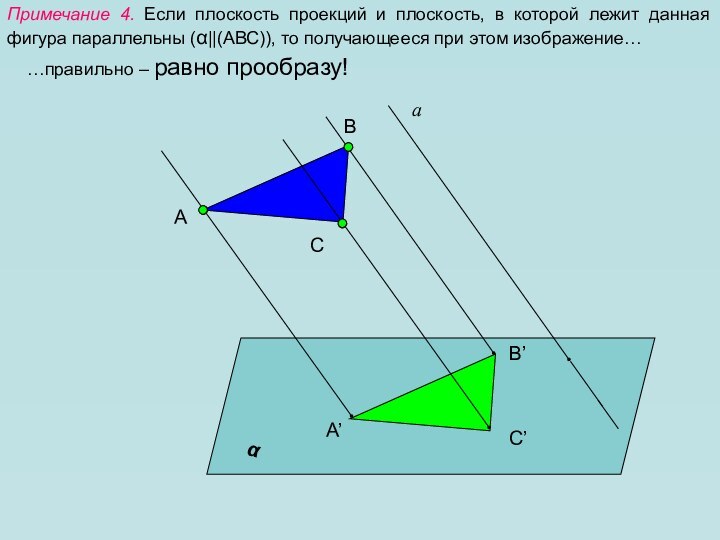
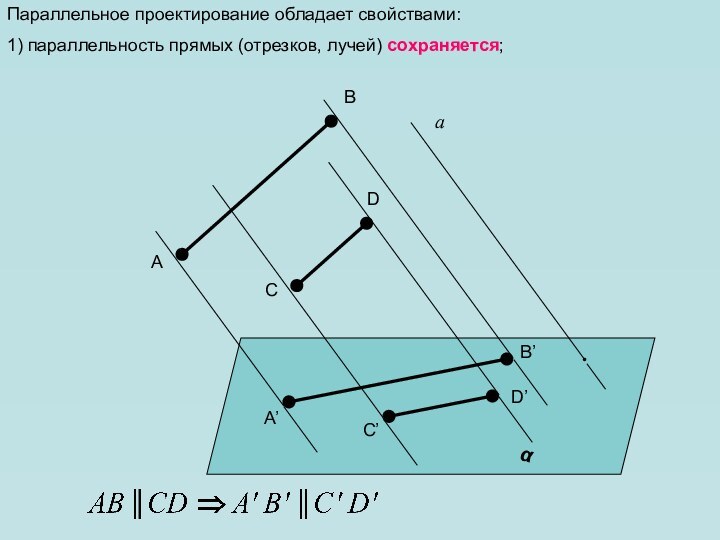
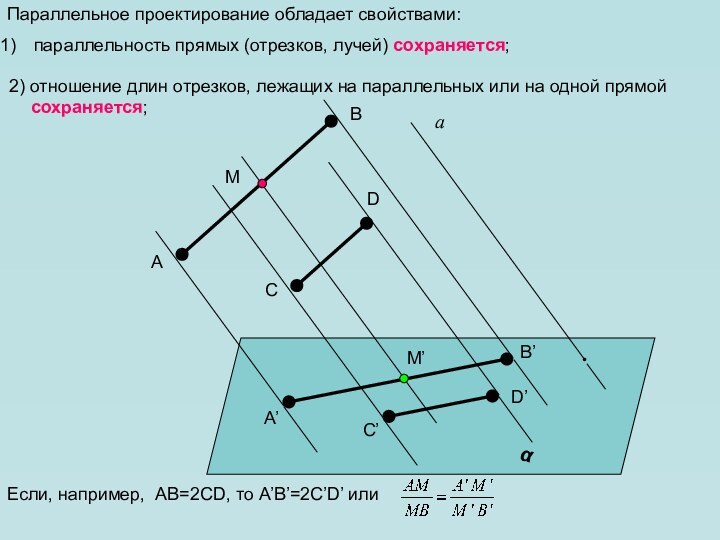
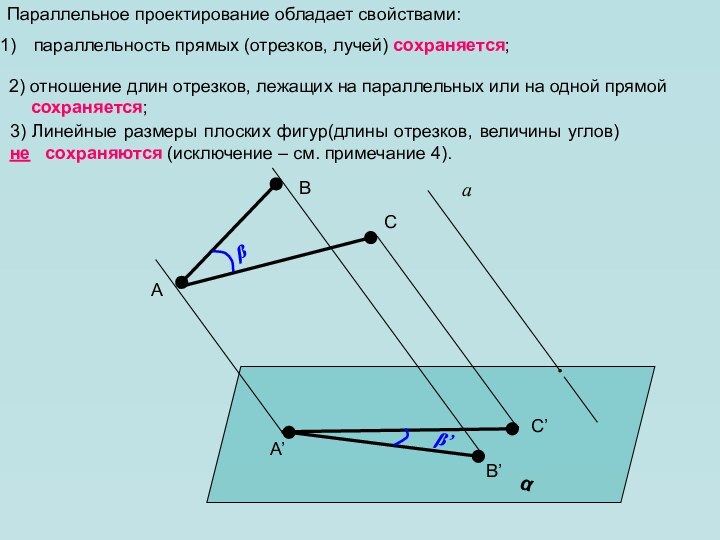
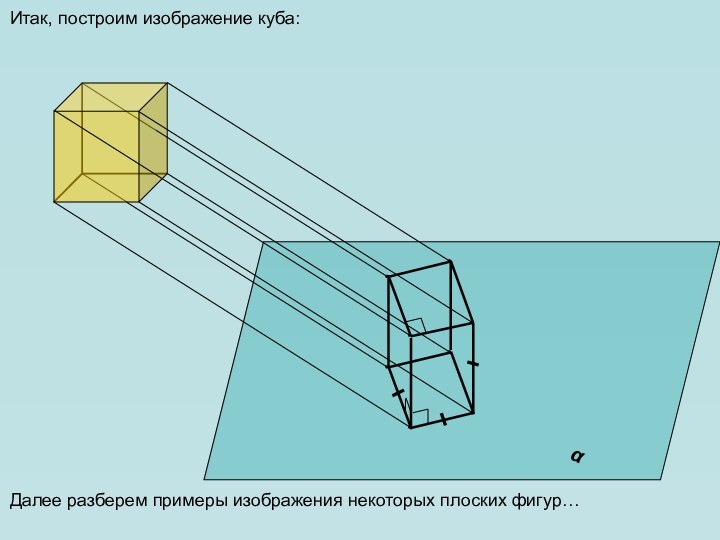
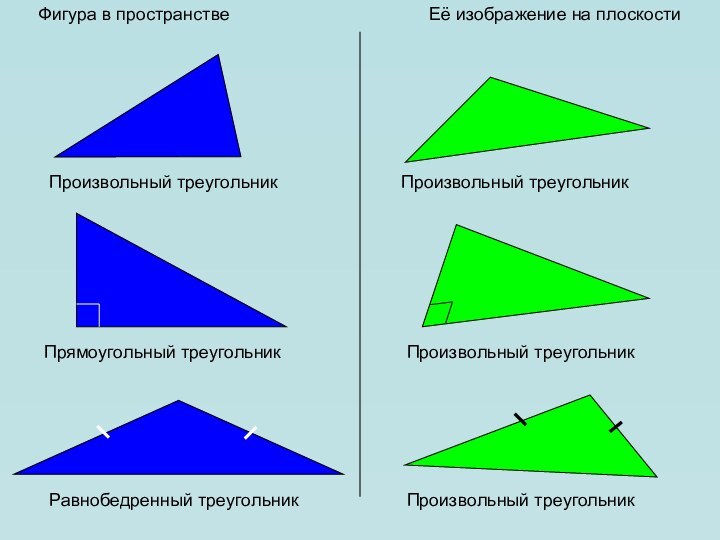
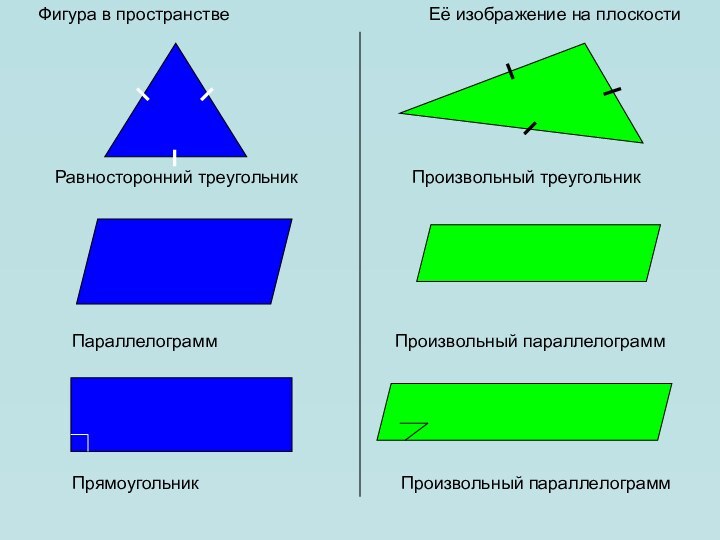
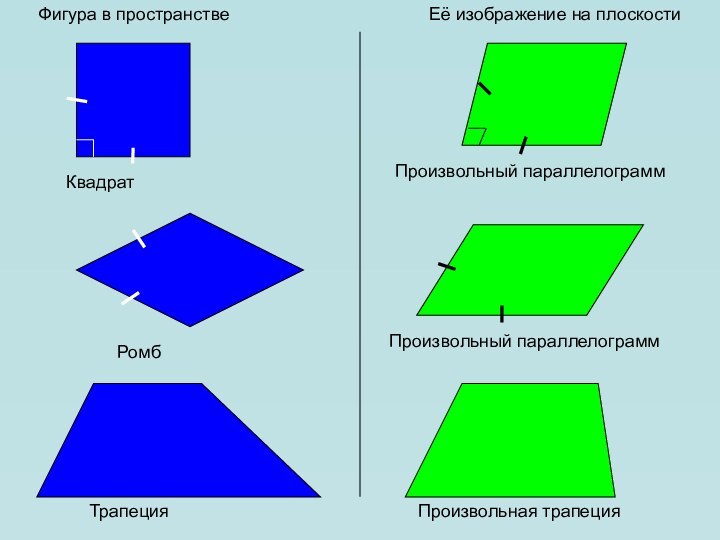
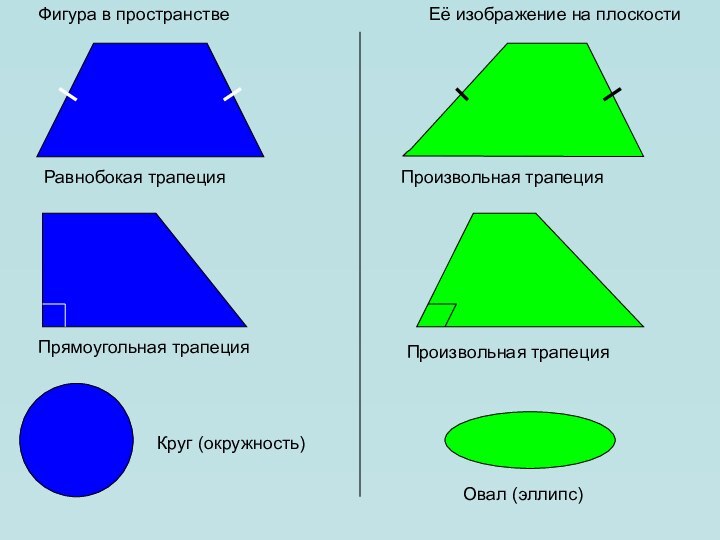
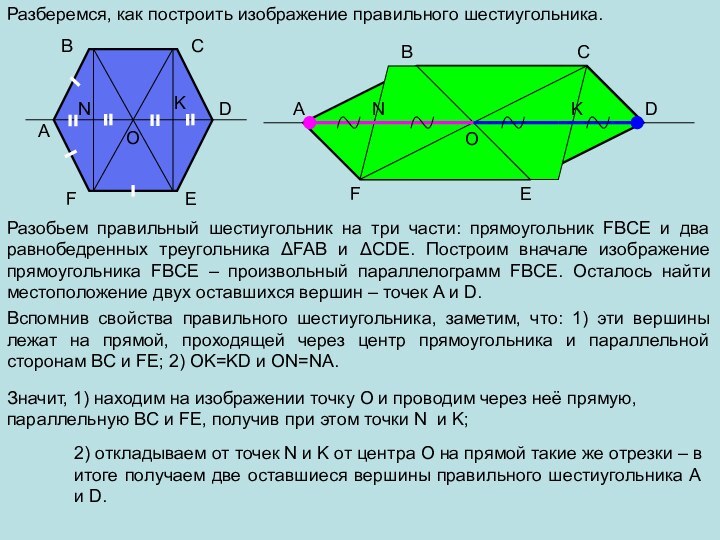
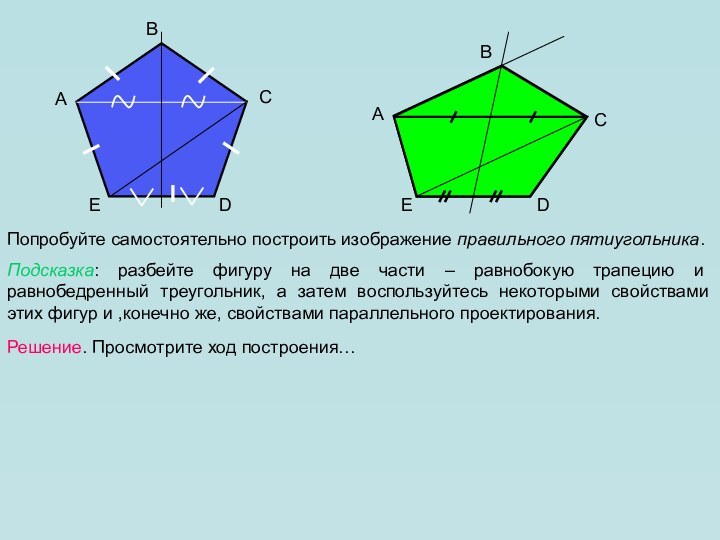
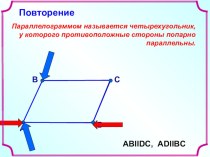
в пространстве. Как всегда нам необходимо уметь изображать геометрические
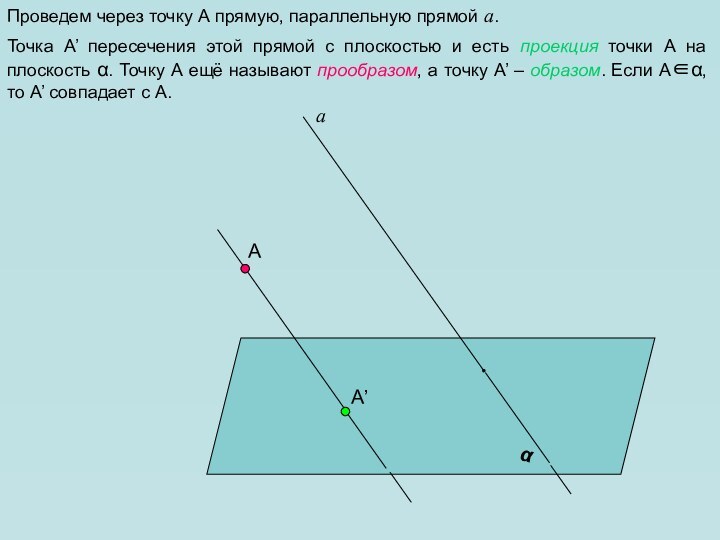
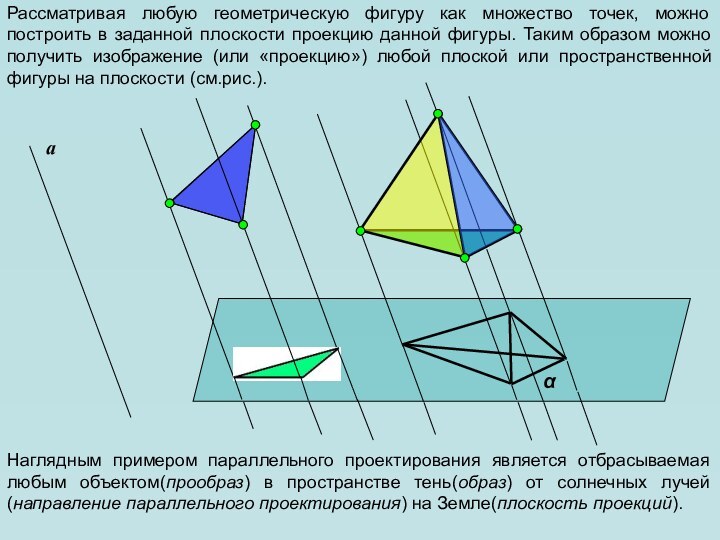
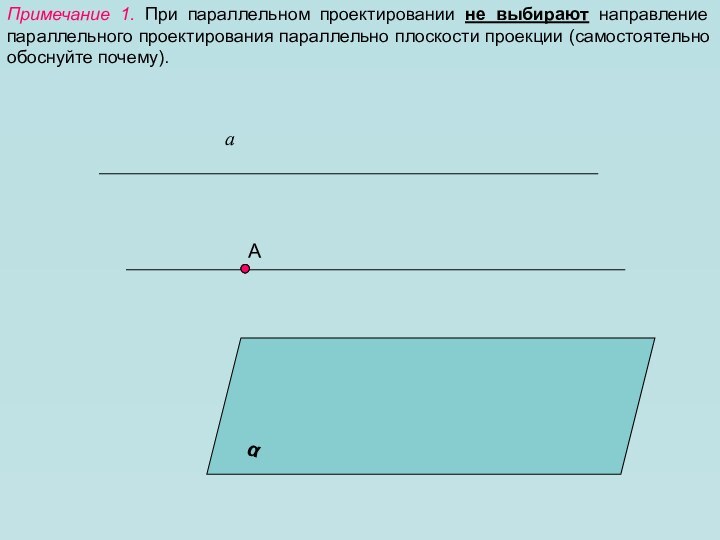
фигуры, причем все чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость?Для решения этой задачи применяется метод параллельного проектирования. Выясним его суть на примере простейшей геометрической фигуры – точки.
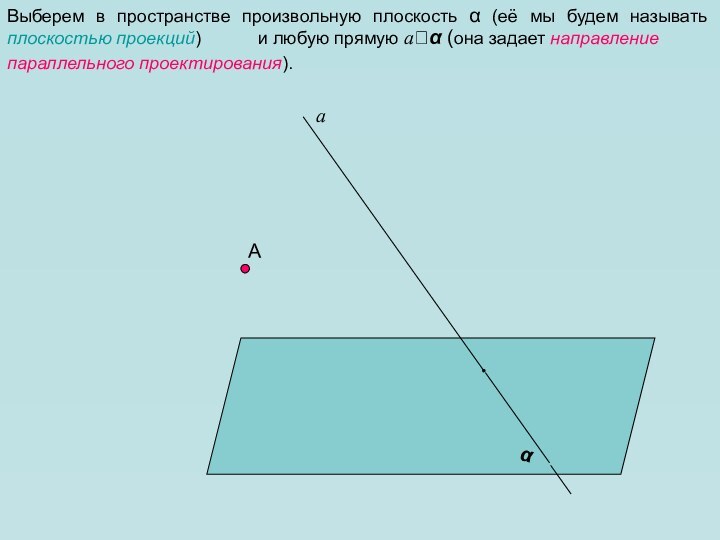
Итак, у нас есть геометрическая фигура в пространстве – точка А.
А