- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Правильные многогранники (10 класс)
Содержание
- 2. МИР МНОГОГРАННИКОВ Выполнила Павлова Александра
- 3. Определение многогранника Многогранник – это
- 5. Правильные многогранники
- 6. Определение Выпуклый многогранник называется правильным, если его гранями
- 7. Почему существуют только 5 правильных многогранниковРаботу выполнил: Борисов Евгений
- 8. Названия правильных многогранников пришли из Греции. В
- 9. Сначала рассмотрим случай, когда грани многогранника -
- 10. Теперь перейдем к квадратным граням. Развертка из
- 11. Для шестиугольников уже три грани дают угол
- 12. Работу выполнилаНечаева Татьяна ТЕТРАЭДР
- 13. Понятие тетраэдраТетраэдр — простейший многогранник, гранями которого являются
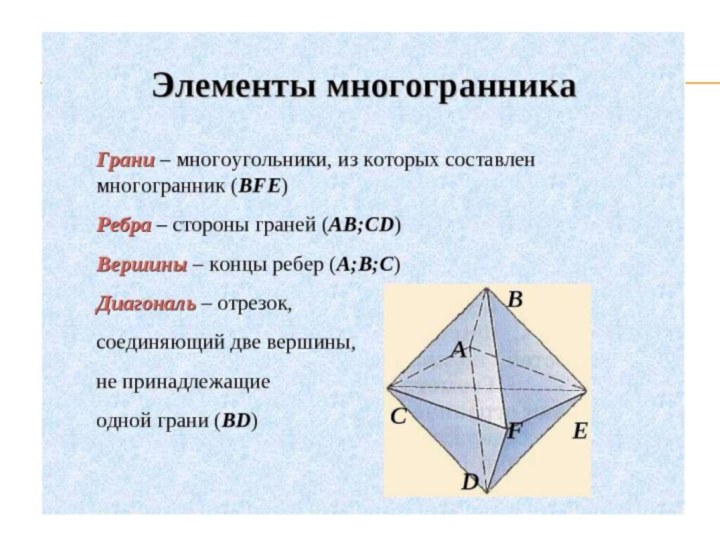
- 14. Элементы тетраэдраГрани (4)ОснованиеРебра (6)Вершины (4)У тетраэдра 4 грани, 4 вершины и 6 ребер
- 15. Многогранник относится к правильным многогранникам и является
- 16. Где встречается тетраэдр?Гигантский тетраэдр для Нового ОрлеанаРазработанное
- 17. Правильный октаэдр Работу выполняла Писарева КристинаУченица 10 «Б» класса
- 18. Древние греки дали многограннику имя по числу
- 19. Октаэдр имеет следующие характеристики: Тип грани
- 20. Где встречаются в жизниМногие природные кубические кристаллы
- 21. Гексаэдр ИкосаэдрРаботу выполнили: Разважная Анастасия и Федотова Анастасия
- 22. Гексаэдр (Куб)- Это правильный многогранник, каждая
- 23. Тела в виде куба (гексаэдра): Кристаллы пиритаПирит
- 24. Икосаэдр- Это правильный выпуклый многогранник.Икосаэдр составлен
- 25. Бактериофа́ги или фа́ги — вирусы, избирательно
- 26. ДодекаэдрПодготовили Плигускина Мария и Галямова Анна
- 27. Додекаэдр - правильный многогранник (платоново тело).
- 28. Элементы симметрии додекаэдра Додекаэдр имеет центр
- 29. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»
- 30. Двойственные правильные многогранникиВЫПОЛНИЛ: Ширяев Максим
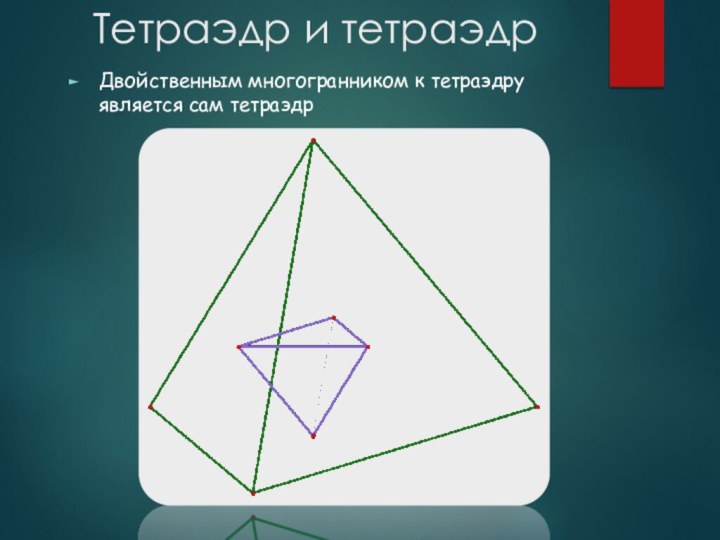
- 31. Двойственные многогранникиДва правильных многогранника называются двойственными, если центры граней одного из них являются вершинами другого.
- 32. Куб и октаэдрЦентры граней куба являются вершинами
- 33. Икосаэдр и додекаэдрАналогично центры граней икосаэдра – вершины додекаэдра, центры граней додекаэдра – вершины икосаэдра
- 34. Тетраэдр и тетраэдрДвойственным многогранником к тетраэдру является сам тетраэдр
- 35. Теорема ЭйлераПодготовили Галямова Анна и Плигускина Мария
- 36. Леонард ЭйлерЛеонард Эйлер - математик, механик и
- 37. Теорема Эйлера для многогранниковВ любом выпуклом многограннике
- 38. Работу выполнили ученицы 10 «Б» класса Петрова Виктория и Бороздина ЯнаПлатоновы тела
- 39. Плато́н - древнегреческий философ,
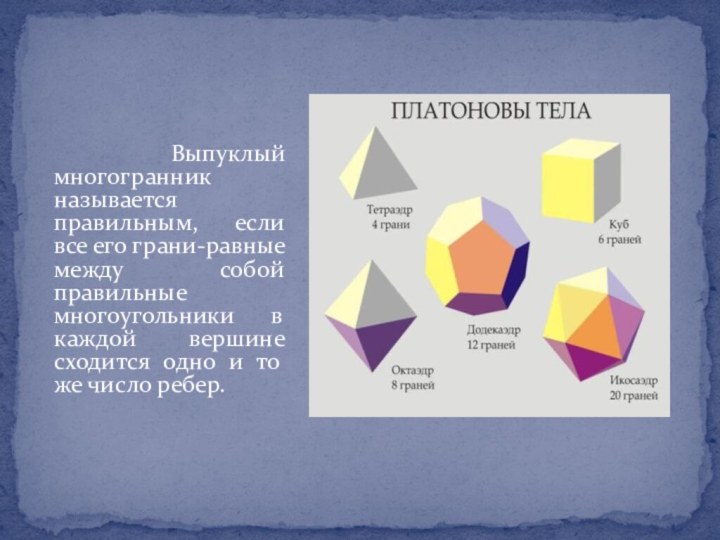
- 40. Выпуклый многогранник называется правильным,
- 41. О существовании всего лишь пяти правильных
- 42. Кубок КеплераРаботу выполнили ученики 10Б класса:Ассоров Денис Мелконян Никита
- 43. 27 декабря 1571г.-15 ноября 1630г.
- 45. Икосаэдро-додекаэдровая структура ЗемлиПодготовили: Коротеев Андрей и Ковлягин Артём
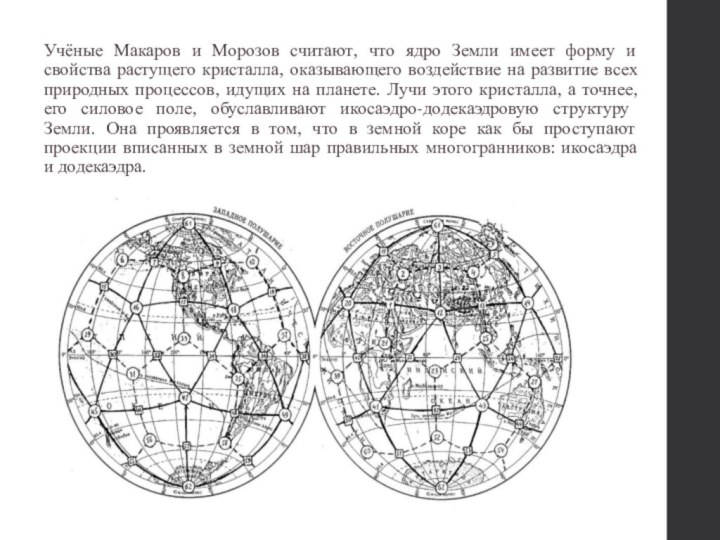
- 46. Учёные Макаров и Морозов считают, что ядро
- 47. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой
- 48. Применение в кристаллографииКарманов ВладУченик 10Б класса
- 49. Понятие о кристаллеКристаллы - это все твердые тела,
- 50. Виды:Например, куб - монокристалл поваренной соли (NaCl),
- 51. Виды:Молекулы воды имеют форму тетраэдраКристаллы пирита имеют
- 52. Техника жестких реберРабота Хромова Георгия 10 Б
- 53. итальянский художник и учёный, изобретатель, писатель, музыкант, один из
- 54. Многие художники разных эпох и стран испытывали
- 55. Строго говоря, грани не изображаются вовсе, они
- 56. Такая техника позволяет зрителю, во-первых, безошибочно определить,
- 57. Техника жестких ребер в искусстве
- 58. Работы Фра Джовани да Верона,созданные для церкви в Вероне
- 59. «Тайная Вечеря»Сальвадор Дали
- 60. Титульный лист книги Ж. Кузена «Книга о перспективе»Надгробный памятникв кафедральном соборе Солсбери
- 61. Графические фантазии Эшера
- 62. «Порядок и хаос»«Двойной планетоид» «Рептилии»«Звезды»
- 63. Работу выполнили: Николаева Анастасия, Устинова ВикторияТела Архимеда
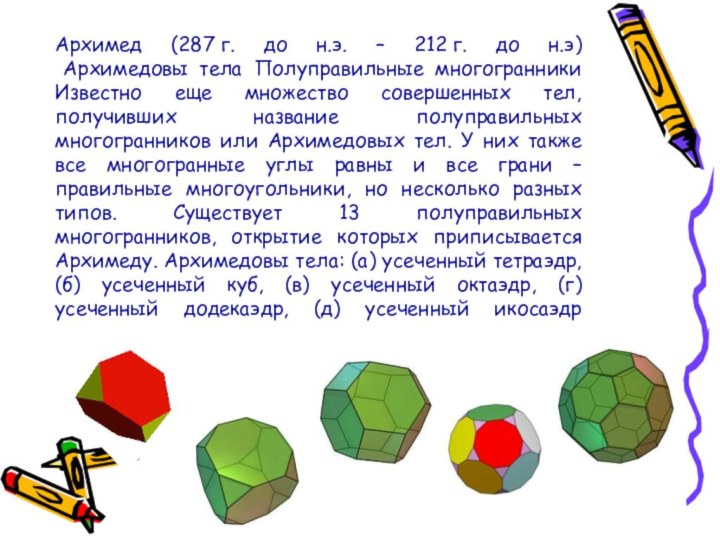
- 64. Архимед (287 г. до н.э. – 212 г. до
- 65. Итак, как же сконструировать
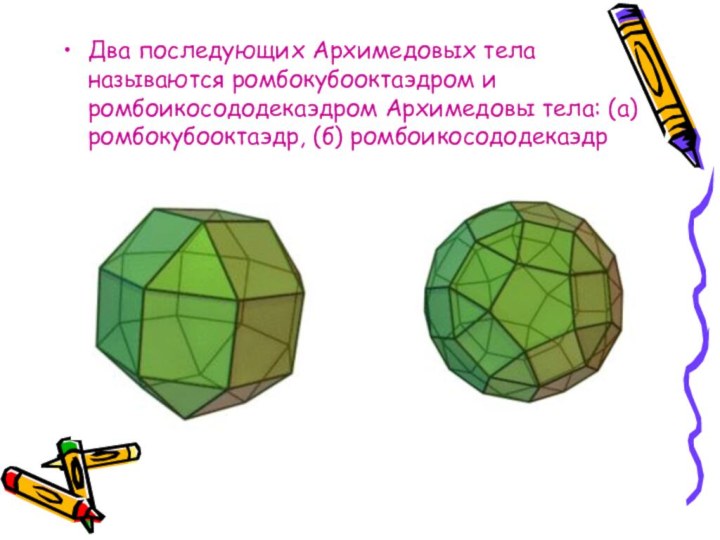
- 66. Два последующих Архимедовых тела называются ромбокубооктаэдром и ромбоикосододекаэдром Архимедовы тела: (а) ромбокубооктаэдр, (б) ромбоикосододекаэдр
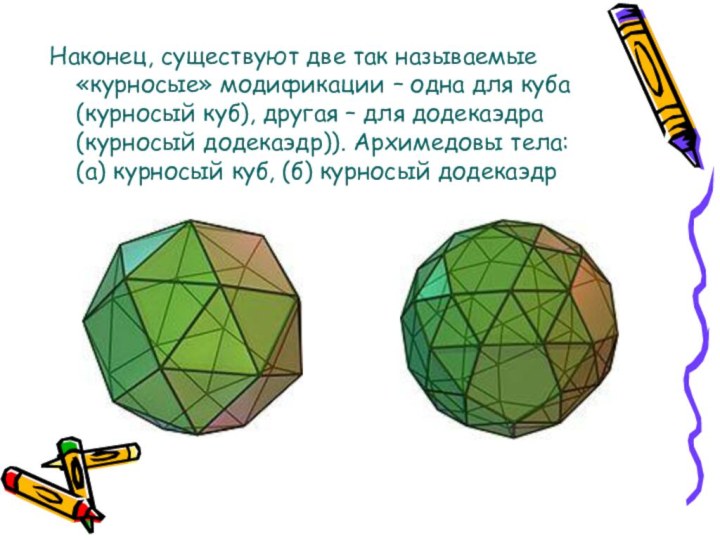
- 67. Наконец, существуют две так называемые «курносые» модификации
- 68. Скачать презентацию
- 69. Похожие презентации






















































Слайд 3
Определение многогранника
Многогранник – это часть
пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединённых таким
образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника.
Слайд 6
Определение
Выпуклый многогранник называется правильным, если его гранями являются равные
правильные многоугольники, и в каждой вершине сходится одинаковое число
гранейСлайд 8 Названия правильных многогранников пришли из Греции. В дословном
переводе с греческого «тетраэдр», «октаэдр», «гексаэдр», «додекаэдр», «икосаэдр» означают:
«четырехгранник», «восьмигранник», «шестигранник», «двенадцатигранник», «двадцатигранник». Этим красивым телам посвящена 13-я книга «Начал» Евклида.Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое. Рассмотрим развертку вершины такого многогранника. Каждая вершина может принадлежать трем и более граням.
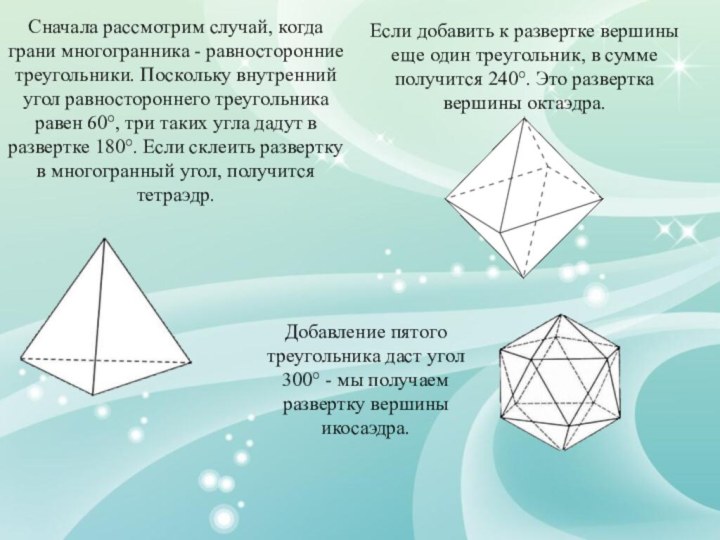
Слайд 9 Сначала рассмотрим случай, когда грани многогранника - равносторонние
треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три
таких угла дадут в развертке 180°. Если склеить развертку в многогранный угол, получится тетраэдр.Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра.
Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра.
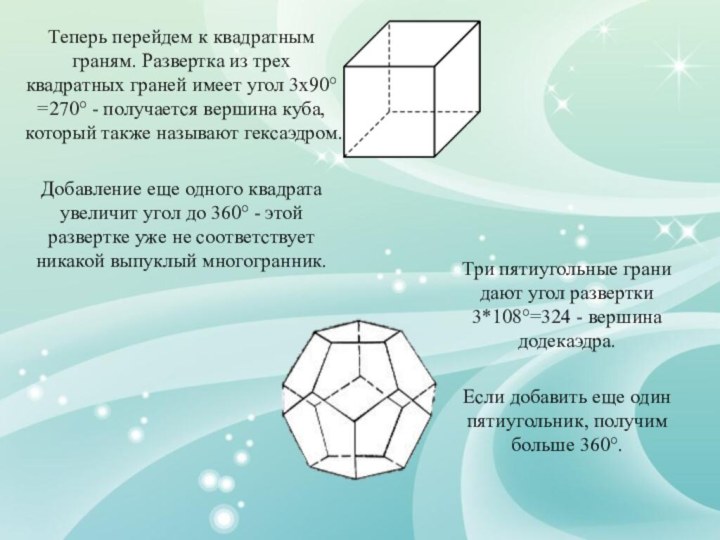
Слайд 10 Теперь перейдем к квадратным граням. Развертка из трех
квадратных граней имеет угол 3x90°=270° - получается вершина куба,
который также называют гексаэдром.Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра.
Если добавить еще один пятиугольник, получим больше 360°.
Слайд 11 Для шестиугольников уже три грани дают угол развертки
3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не
существует.Таким образом, существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
Слайд 13
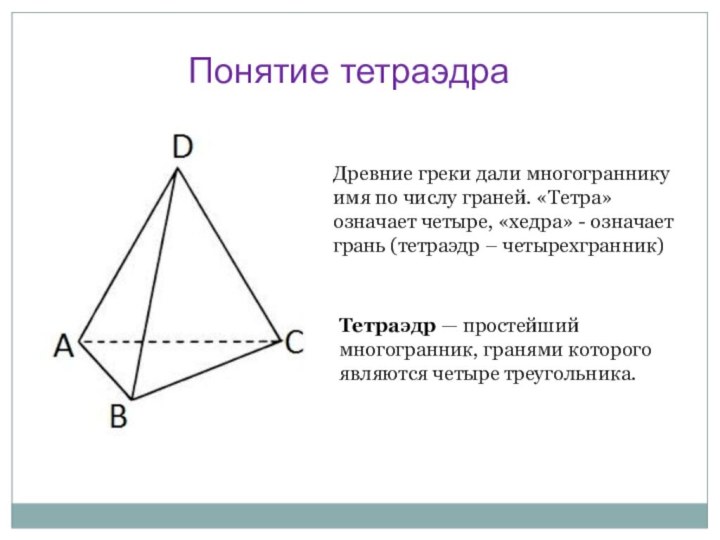
Понятие тетраэдра
Тетраэдр — простейший многогранник, гранями которого являются четыре
треугольника.
Древние греки дали многограннику имя по числу граней.
«Тетра» означает четыре, «хедра» - означает грань (тетраэдр – четырехгранник)
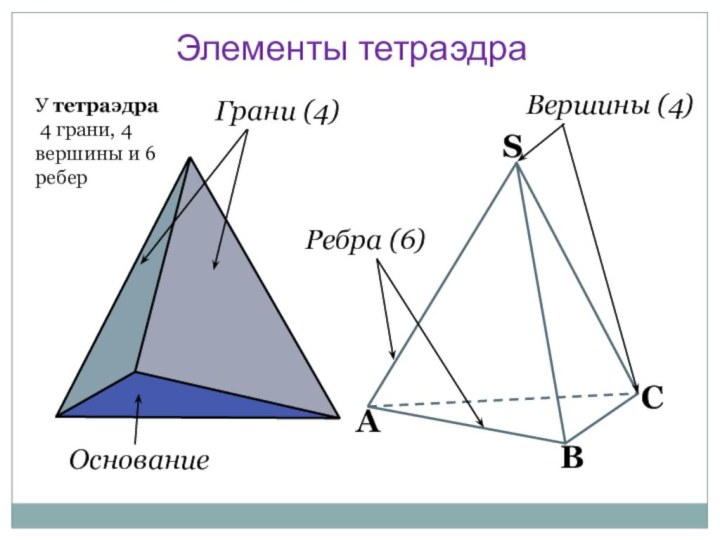
Слайд 14
Элементы тетраэдра
Грани (4)
Основание
Ребра (6)
Вершины (4)
У тетраэдра 4 грани, 4 вершины
и 6 ребер
Слайд 15 Многогранник относится к правильным многогранникам и является одним
из пяти платоновых тел.
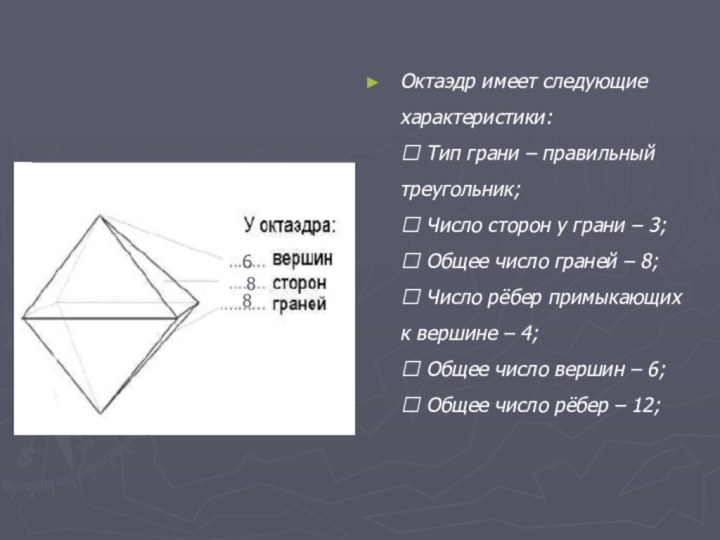
Тетраэдр имеет следующие характеристики:
Тип грани – правильный треугольник;
Число
сторон у грани – 3;Общее число граней – 4;
Число рёбер примыкающих к вершине – 3;
Общее число вершин – 4;
Общее число рёбер – 6;
Каждое ребро принадлежит двум граням;
Все двугранные углы равны.
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Слайд 16
Где встречается тетраэдр?
Гигантский тетраэдр для Нового Орлеана
Разработанное для
Нового Орлеана «здание-город» NOAH (New Orleans Arcology Habitat) возвышается
на 365 метров, включает в себя 20000 квартир, суммарная жилая площадь которых равна 2 040 000 кв.м. Здание использует экологичное энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре помещаются коммерческие организации, три отеля, культурные объекты, школа, больницы и казино. И, учитывая место, под которое создавался проект, его немаловажная особенность — способность держаться на плаву.Слайд 18 Древние греки дали многограннику имя по числу граней.
«Окто» означает восемь, «хедра» - означает грань (октаэдр –
восьмигранник). Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел. Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°. Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.Слайд 19 Октаэдр имеет следующие характеристики: Тип грани – правильный
треугольник; Число сторон у грани – 3; Общее число
граней – 8; Число рёбер примыкающих к вершине – 4; Общее число вершин – 6; Общее число рёбер – 12;6
8
8
Слайд 20
Где встречаются в жизни
Многие природные кубические кристаллы имеют
форму октаэдра. Это алмаз, хлорид натрия, флюорит, шпинель.
Слайд 22
Гексаэдр (Куб)-
Это правильный многогранник, каждая грань
которого представляет собой квадрат.
Таким образом, куб имеет:
8 вершин
12 рёбер
6
граней3 грани при вершине
Сумма плоских углов при каждой вершине = 270°
Слайд 23
Тела в виде куба (гексаэдра):
Кристаллы пирита
Пирит —
это серный, или железный, колчедан. Название пирита — происходит
oт греческого слова «пир» — огонь. Древние греки называли его — огнеподобный — за огненно-желтый цвет и способность высекать искры при ударе твердыми (стальными, кремневыми) предметами.
Слайд 24
Икосаэдр-
Это правильный выпуклый многогранник.
Икосаэдр составлен из
двадцати равносторонних треугольников.
Каждая его вершина является вершиной пяти
треугольников.Икосаэдр имеет:
20 граней
12 вершин
30 ребер
5 граней при вершине
Слайд 25 Бактериофа́ги или фа́ги — вирусы, избирательно поражающие
бактериальные клетки. Чаще всего бактериофаги размножаются внутри бактерий и
вызывают их лизис. Как правило, бактериофаг состоит из белковой оболочки и генетического материала одноцепочечной или двуцепочечной нуклеиновой кислотыТела в виде икосаэдра:
Слайд 27
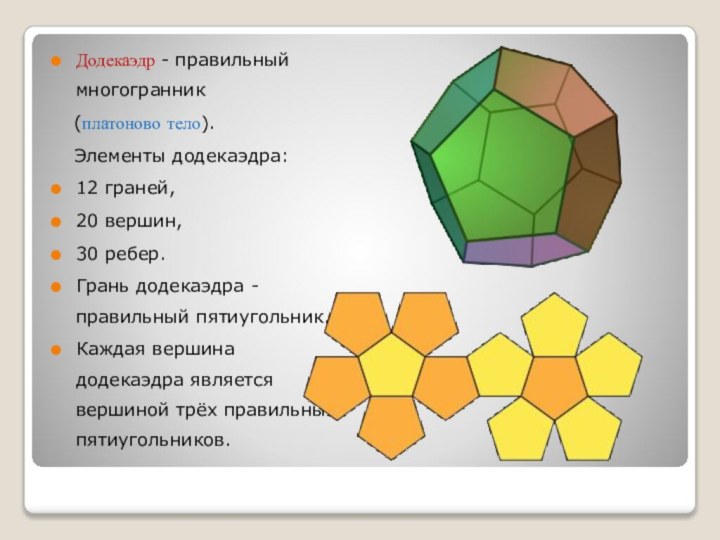
Додекаэдр - правильный многогранник
(платоново тело).
Элементы додекаэдра:
12 граней,
20 вершин,
30 ребер.
Грань
додекаэдра - правильный пятиугольник. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Слайд 28
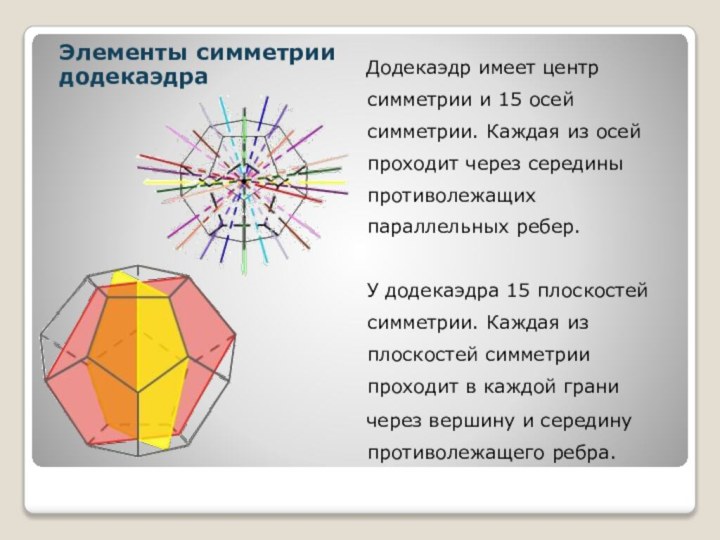
Элементы симметрии додекаэдра
Додекаэдр имеет центр симметрии
и 15 осей симметрии. Каждая из осей проходит через
середины противолежащих параллельных ребер. У додекаэдра 15 плоскостей симметрии. Каждая из плоскостей симметрии проходит в каждой граничерез вершину и середину противолежащего ребра.
Слайд 29
Платон сопоставлял с правильными
многогранниками различные
классические стихии. О додекаэдре Платон писал, что «…его бог определил для
Вселенной и прибегнул к нему в
качестве образца»
Слайд 31
Двойственные многогранники
Два правильных многогранника называются двойственными, если центры
граней одного из них являются вершинами другого.
Слайд 32
Куб и октаэдр
Центры граней куба являются вершинами октаэдра,
в свою очередь центры граней октаэдра являются вершинами куба.
Слайд 33
Икосаэдр и додекаэдр
Аналогично центры граней икосаэдра – вершины
додекаэдра, центры граней додекаэдра – вершины икосаэдра
Слайд 36
Леонард Эйлер
Леонард Эйлер - математик, механик и физик.
Родился в Швейцарии в городе Базель, в семье небогатого
пастора Пауля Эйлера.В конце 1726 года Эйлер был приглашен в Петербургскую Академию Наук и в мае 1727 года приехал в Петербург.
Слайд 37
Теорема Эйлера для многогранников
В любом выпуклом многограннике сумма
числа граней и числа вершин больше числа ребер на
2.Пусть В — число вершин выпуклого многогранника, Р — число его ребер и Г — число граней. Тогда верно равенство
В – Р + Г = 2
Слайд 39 Плато́н - древнегреческий философ, ученик
Сократа, учитель Аристотеля. Платон — первый философ, чьи сочинения
дошли до нас не в кратких отрывках, цитируемых другими, а полностью.Слайд 40 Выпуклый многогранник называется правильным, если
все его грани-равные между собой правильные многоугольники в каждой
вершине сходится одно и то же число ребер.Слайд 41 О существовании всего лишь пяти правильных многогранников
знали еще в Древней Греции. Великий древнегреческий мыслитель Платон
считал, что четыре из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа») или «пятая сущность».Слайд 46 Учёные Макаров и Морозов считают, что ядро Земли
имеет форму и свойства растущего кристалла, оказывающего воздействие на
развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.Слайд 47 Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки;
62 вершины и середины рёбер многогранников, называемых авторами узлами,
обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.
Слайд 49
Понятие о кристалле
Кристаллы - это все твердые тела, имеющие
форму многогранника, возникающую в результате упорядоченного расположения атомов. Кристаллографию
называют наукой о кристаллах, кристаллических природных телах. Она изучает форму, внутреннее строение, происхождение, распространение и свойства кристаллических веществ.
Слайд 50
Виды:
Например, куб - монокристалл поваренной соли (NaCl), октаэдр
- монокристалл алюмокалиевых квасцов, одна из форм кристаллов алмаза
- октаэдр
Слайд 51
Виды:
Молекулы воды имеют форму тетраэдра
Кристаллы пирита имеют форму
додекаэдра
Поваренная соль состоит из кристаллов в форме куба
Слайд 53 итальянский художник и учёный, изобретатель, писатель, музыкант, один из крупнейших
представителей искусства эпохи Возрождения, яркий пример «универсального человека»
Леонардо да
Винчи Слайд 54 Многие художники разных эпох и стран испытывали постоянный
интерес к изучению и изображению многогранников. Пик этого интереса
приходится, конечно, на эпоху Возрождения. Изучая явления природы, художники Возрождения стремились найти опирающиеся на опыт науки способы их изображения. Учения о перспективе, светотени и пропорциях позволяют художнику воссоздавать на плоскости трехмерное пространство, добиваться впечатления рельефности предметов. Для некоторых мастеров Возрождения многогранники являлись просто удобной моделью для тренировки мастерства перспективы.Эпоха Возрождения





























