- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии в 8 классе по теме Теорема Пифагора
Содержание
- 2. Историческая справка. Существует замечательное соотношение между гипотенузой
- 3. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы
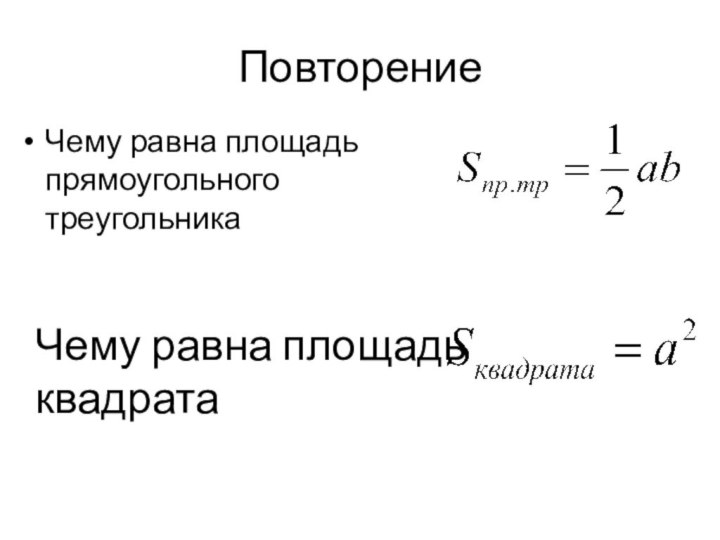
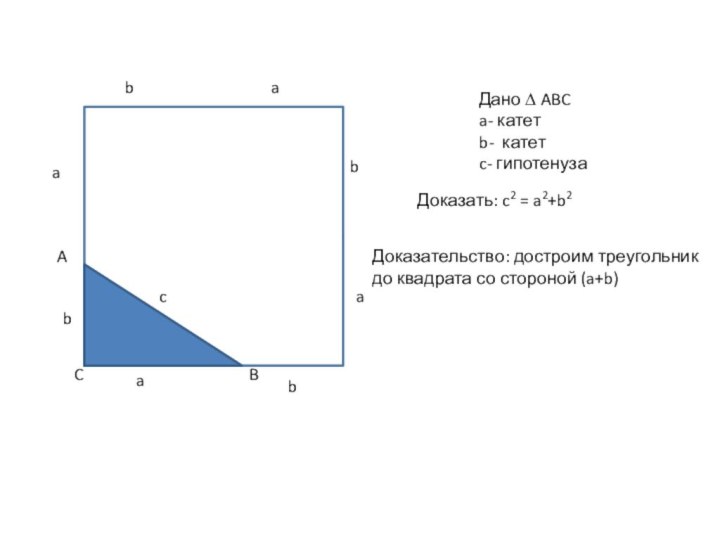
- 4. Дано ∆ ABCa- катетb- катетc- гипотенузаДоказать: c2 = a2+b2Доказательство: достроим треугольник до квадрата со стороной (a+b)aaabbb
- 5. Дано ∆ ABCa- катетb- катетc- гипотенузаДоказать: c2
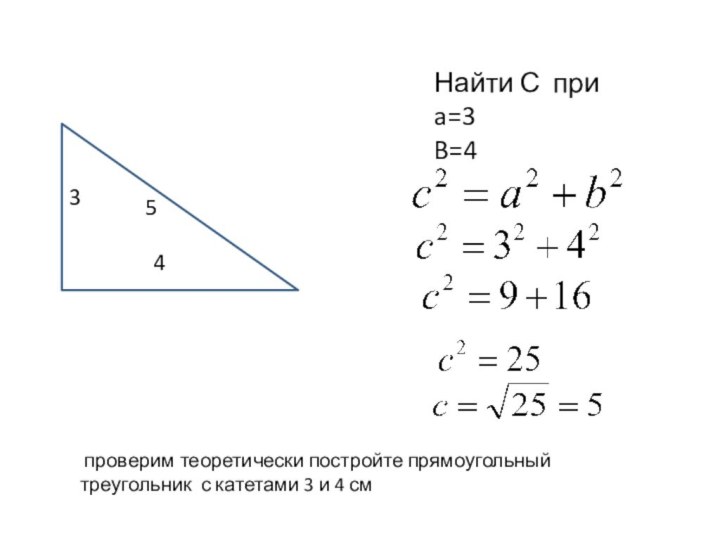
- 6. проверим теоретически постройте прямоугольный треугольник с катетами 3 и 4 смНайти С при a=3B=4
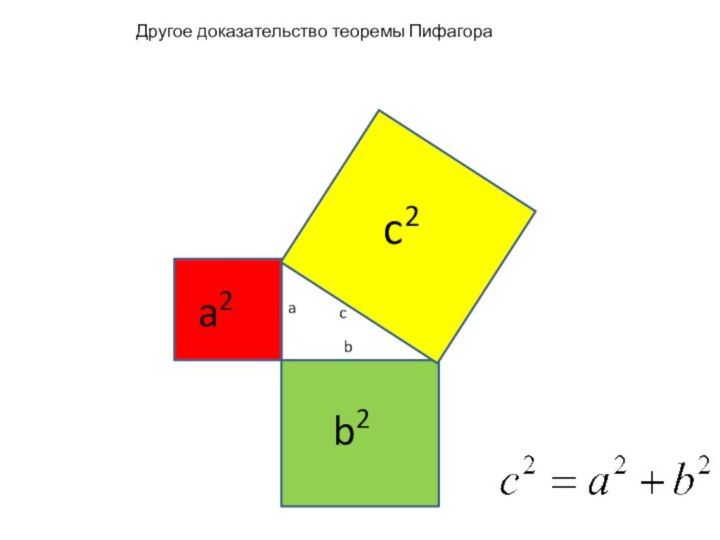
- 7. Другое доказательство теоремы Пифагора
- 8. ЗакреплениеРешить №483(а,б)№484(а,б)№487
- 9. Скачать презентацию
- 10. Похожие презентации
Историческая справка. Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость которого была доказана древнегреческим философом и математиком Пифагором (VI в. до н.э.). Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это





Слайд 3
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
Пусть с –гипотенуза, а- катет, b-другой
катет. Тогда:
Слайд 4
Дано ∆ ABC
a- катет
b- катет
c- гипотенуза
Доказать: c2 =
a2+b2
Доказательство: достроим треугольник до квадрата со стороной (a+b)
a
a
a
b
b
b
Слайд 5
Дано ∆ ABC
a- катет
b- катет
c- гипотенуза
Доказать: c2 =
a2+b2
Доказательство:
1)достроим треугольник до квадрата со стороной (a+b)
S=(a+b)2=
=2ab+c2
2) Найдём
площадь полученного квадрата двумя способамиЧто и требовалось доказать