- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок Векторы в пространстве
Содержание
- 2. Векторы
- 3. ВекторыНазад
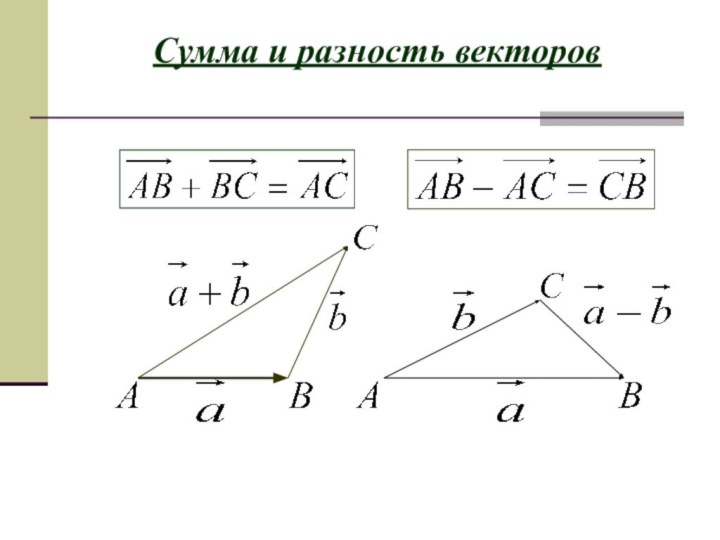
- 4. Сумма и разность векторов
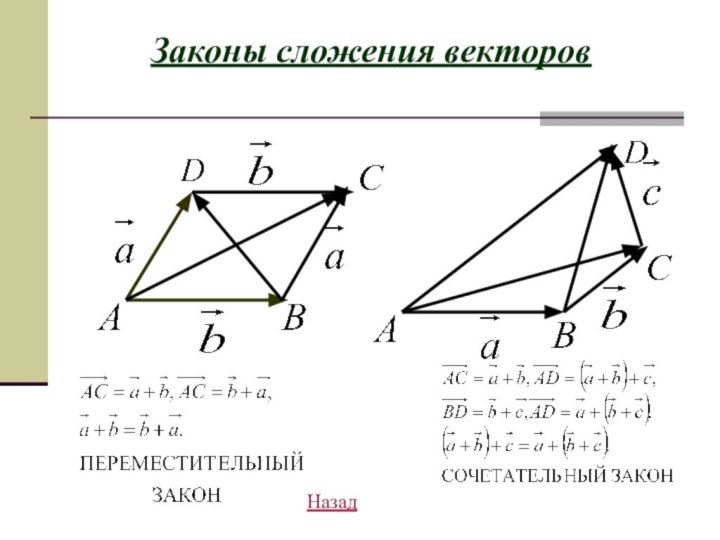
- 5. Законы сложения векторовНазад
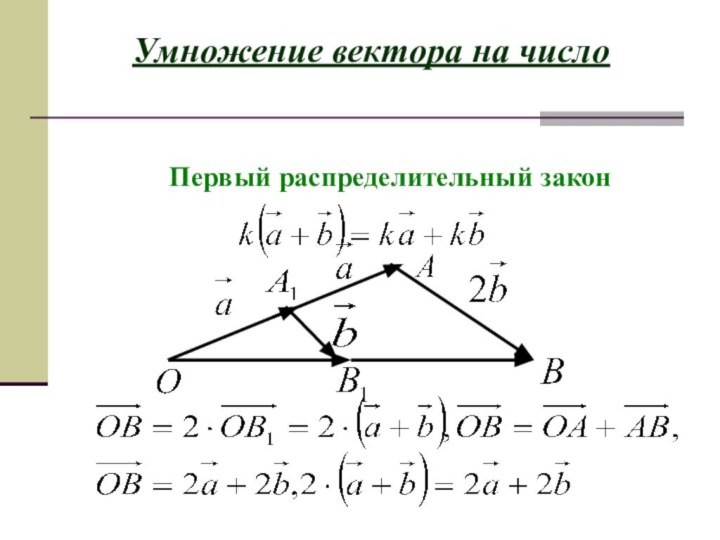
- 6. Умножение вектора на число
- 7. Умножение вектора на число
- 8. Умножение вектора на числоНазад
- 9. Компланарные векторыНазад
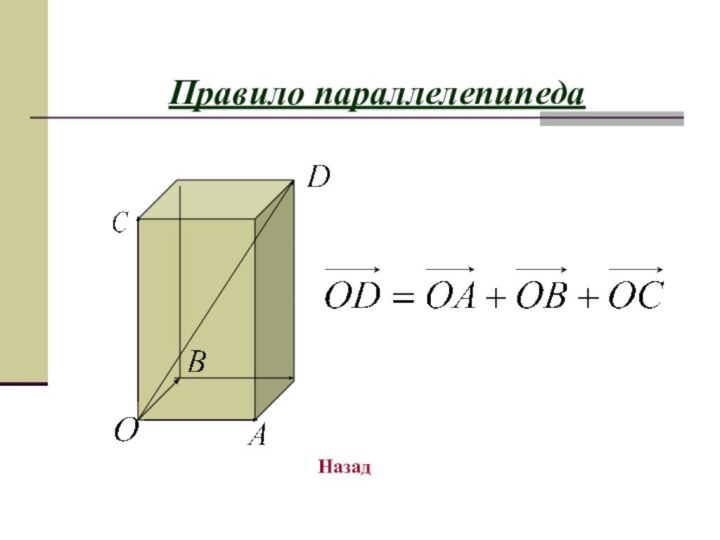
- 10. Правило параллелепипедаНазад
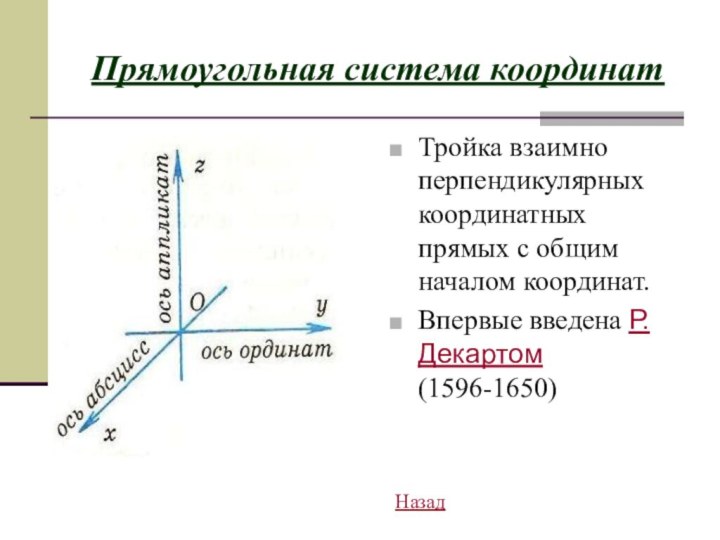
- 11. Прямоугольная система координатТройка взаимно перпендикулярных координатных прямых с общим началом координат.Впервые введена Р.Декартом(1596-1650)Назад
- 12. Координаты точкиКаждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых координатами точки в пространстве Назад
- 13. Координаты вектораВекторы (i. j. k) единичные векторыЛюбой вектор можно разложить по координатным векторамНазад
- 14. Длина вектораНазад
- 15. Скалярное произведение векторовНазад
- 16. Свойства скалярного произведения. Угол между векторами.Назад
- 17. Самостоятельная работаНазад
- 18. Скачать презентацию
- 19. Похожие презентации
Векторы