Презентация на тему Моделирование в стереометрии Построение сечений

прямую, не лежащую в
этой плоскости, то все

три прямые пересекаются вместе в одной точке.

построение сечений
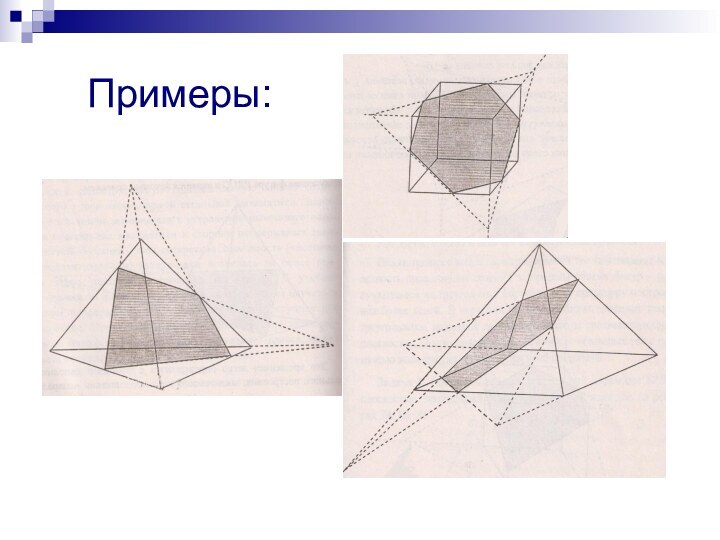
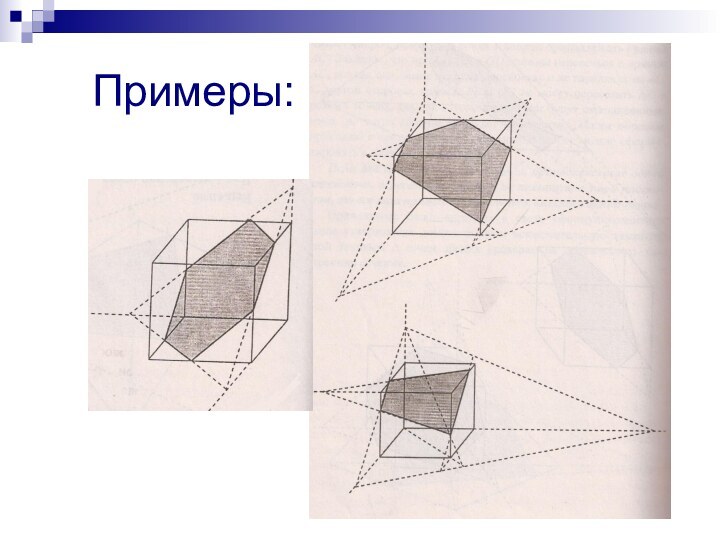
Рассмотренные выше примеры

сечения тел показывают полезность продолжения сечений за пределы объема фигур – получающиеся их треугольные формы делают процедуру построения более ясной. В черчении прямые, которые образуют такие треугольники, называют следами сечения на соответствующих плоскостях. Процедура нахождения сечений объемных тел с помощью этих прямых и называется методом следов.

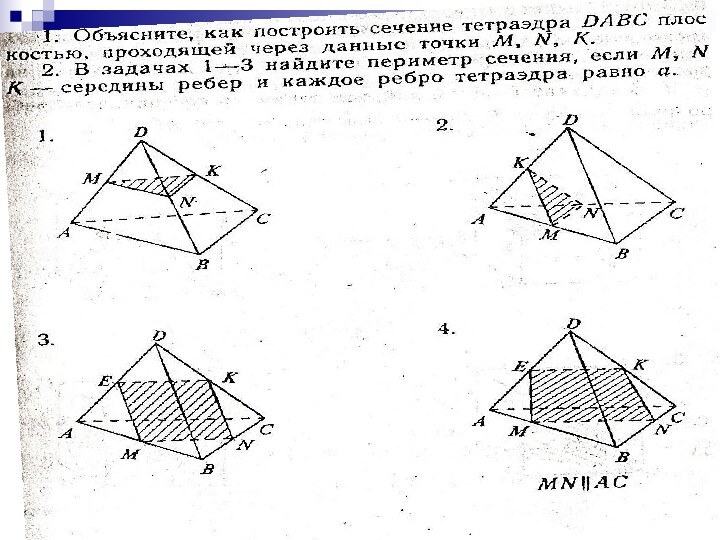
Задача 1
Построить сечение треугольной пирамиды SABC плоскостью,

проходящей через точки P,Q ,R, лежащие на рёбраx SA,SB,AC.

Решение.
Для определения следа сечения на плоскости основания пирамиды

SABC заметим ,что одна его точка R задана по условию задачи, а другую точку U можно найти с помощью продолжения отрезкаPQ до пересечения с прямой AB, которая принадлежит основанию ABC. Соединив точки U и R, получим след сечения, пересечение которого с ребром BC дает искомую вершину T четырехугольной плоской фигуры сечения PRTQ.

Задача 2
Построить сечение четырехугольной пирамиды SABCD плоскостью,

проходящей через точки P, Q, R, лежащие на боковых ребрах SA, SB, SC.

Решение
Очевидно, необходимо определить точки пересече-ния плоскости сечения с

нижними ребрами пирамиды SABCD, т. е. достаточно найти след сечения на плоскости основания ABCD.
Продолжая отрезки PQ и QR до пересечения с прямыми АВ и ВС, принадлежащими плоскости ABCD , найдем точки V и U. Соединив эти точки, получим след плоскос-ти сечения на грани ABCD пирамиды. Точки пересече-ния T и W следа со сторона-ми основания ABCD и являются искомыми верши-нами сечения пирамиды ABCD.

три заданные точки M, O, N, лежащие на соседних

ребрах АВ, ВВ1 , В1С1.

Решение:
Очевидно, что прямая ОМ представляет собой след плоскости

сечения призмы на её грани AA1ВB1. Точка S её пересечение с продолжением ребра AA1 принадлежит следу плоскости сечение на грани AA1СC1. Чтобы найти другую точку V этого следа, продолжим прямую ON до пересечения с продолжением ребра СC1. Соединив эти точки, получим линию сечения, пересекающую ребра грани AA1ВB1 в точках T и U.
Пятиугольник MONUT –
искомое сечение.

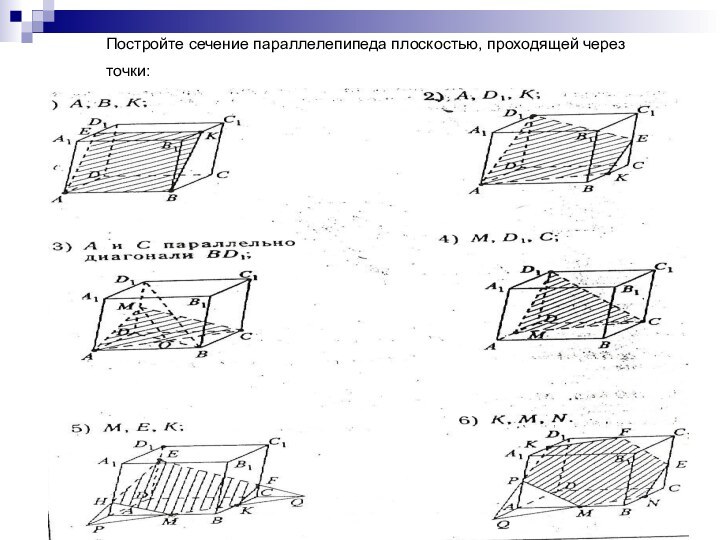
Задача 4
Построить сечение куба ABCDA1B1C1D1, проходящее через

три точки P, Q, R, лежащие на соседних ребрах А1В1, В1С1, АА1.

Решение:
Соединим точки P и Q, P и

R между собой. Прямая РR представляет собой след плоскости сечения куба на плоскости его грани AA1ВB1.
Точки пересечения U и S этого следа с продолжениями ребер АВ и ВB1 являются точками следов сечения на гранях ABCD и ВB1СС1 . Так как точка Q тоже принадлежит грани ВB1СС1 ,находим след сечения SТ на этой грани. Соединив точки Т и U, получаем третий след сечения на плоскости ABCD. Точки пересечения найденных трех следов с ребрами куба и определяют его шестиугольное сечение PRVWHQ.