- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора, 8 класс
Содержание
- 2. Цели урокаСформулировать и доказать теорему Пифагора;Отработать навыки применения теоремы при решении задач.*http://aida.ucoz.ru
- 3. Что изображено? Вопросы Чему равна сумма острых
- 4. Докажите, что треугольники равны.
- 5. ABCDESABCDE = SABC + SADC + SADE
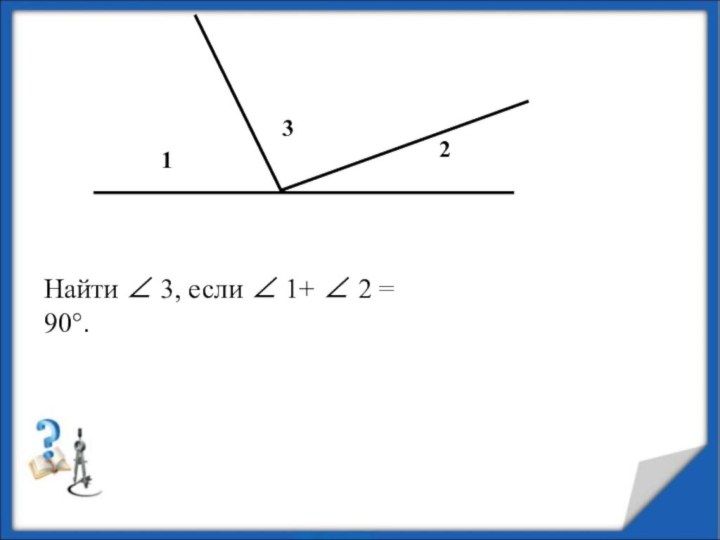
- 6. Найти ∠ 3, если ∠ 1+ ∠ 2 = 90°.
- 7. Решите устноCABДано: ∆
- 8. Нужно знать зависимость между катетами и гипотенузой
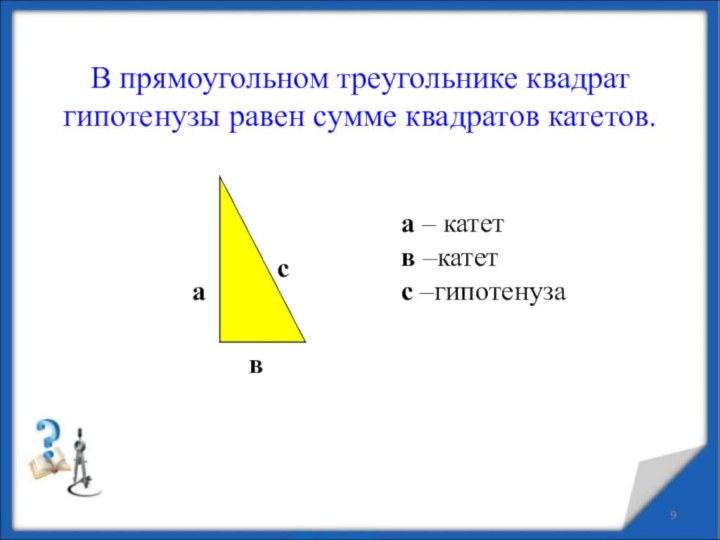
- 9. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.а – катетв –катетс –гипотенузаавс
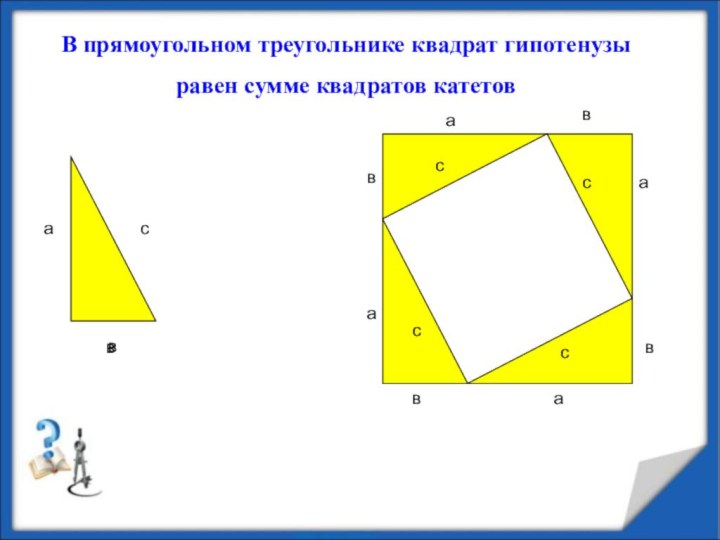
- 10. асвссссввввааааВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовв
- 11. Доказательство теоремы Дано: прямоугольный треугольник
- 12. Формулировка теоремы « Доказать, что
- 13. Немного истории Для нас Пифагор –
- 14. Пифагор Самосский - это
- 15. Значение теоремы ПифагораТеорема Пифагора- это одна
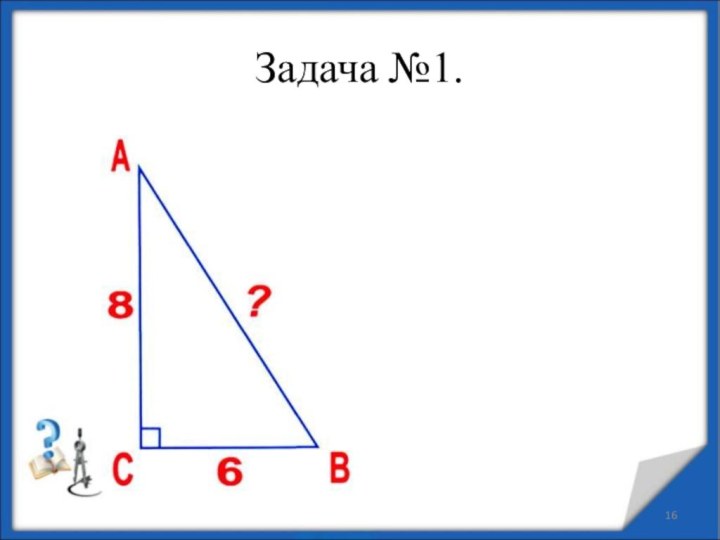
- 16. Задача №1.
- 17. Решение задачи №1
- 18. Задача №2.
- 19. Решение задачи №2DCE − прямоугольный с
- 20. Задача №3Для крепления мачты нужно установить 4
- 21. Итог урока 1. Возможно было решение задач
- 22. Стих о теореме Пифагора Если дан
- 23. Скачать презентацию
- 24. Похожие презентации
Цели урокаСформулировать и доказать теорему Пифагора;Отработать навыки применения теоремы при решении задач.*http://aida.ucoz.ru
















Слайд 2
Цели урока
Сформулировать и доказать теорему Пифагора;
Отработать навыки применения
теоремы при решении задач.
Слайд 3
Что изображено?
Вопросы
Чему равна сумма острых углов
в прямоугольном треугольнике?
∠А + ∠В = 90°
Чему равна площадь
этого треугольника?Как называются стороны АС и ВС?
Слайд 8 Нужно знать зависимость между катетами и гипотенузой в
прямоугольном треугольнике.
Эту зависимость
подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора. Слайд 9 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов.
а – катет
в –катет
с –гипотенуза
а
в
с
Слайд 10
а
с
в
с
с
с
с
в
в
в
в
а
а
а
а
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов
катетов
в
Слайд 11
Доказательство теоремы
Дано: прямоугольный треугольник
а, в – катеты, с – гипотенуза
Доказать: с2=
а2 + в2 Доказательство:
Достроим треугольник до квадрата со стороной а+в;
S=(а+в)2 - площадь квадрата
Четыре прямоугольных треугольника, S = ½ ав
S= 4*1/2ав+с2 =2ав+с2
(а+в)2 = 2ав+с2
с2= а2 + в2
а
а
а
а
с
с
с
с
в
в
в
в
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 12
Формулировка
теоремы
« Доказать, что квадрат, построенный
на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
катетах»« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
Слайд 13
Немного истории
Для нас Пифагор – математик.
В древности было иначе. Геродот называет его "выдающимся софистом",
то есть учителем мудрости. Для своих современников Пифагор прежде всего был религиозным пророком, воплощением высшей божественной мудрости. Пифагор был разносторонней личностью. Он занимался и медициной, и музыкой, и астрономией, а так же был четыре раза подряд олимпийским чемпионом.Слайд 14 Пифагор Самосский - это древнегреческий
математик, философ и мистик, родоначальник школы пифагорейцев. Годы его
жизни - 570-490 гг. до н. э.Немного истории
Слайд 15
Значение теоремы Пифагора
Теорема Пифагора- это одна из
самых важных теорем геометрии. Значение её состоит в том,
что из неё или с её помощью можно вывести большинство теорем геометрии.
Слайд 17
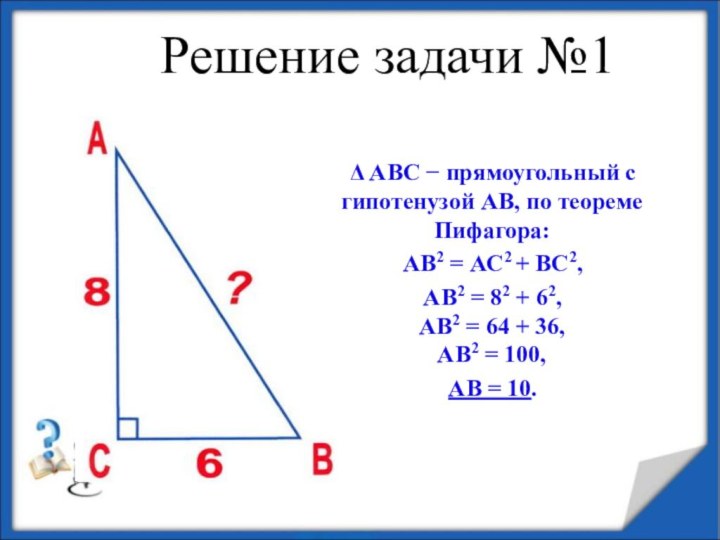
Решение задачи №1
Δ АВС − прямоугольный с гипотенузой АВ, по теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
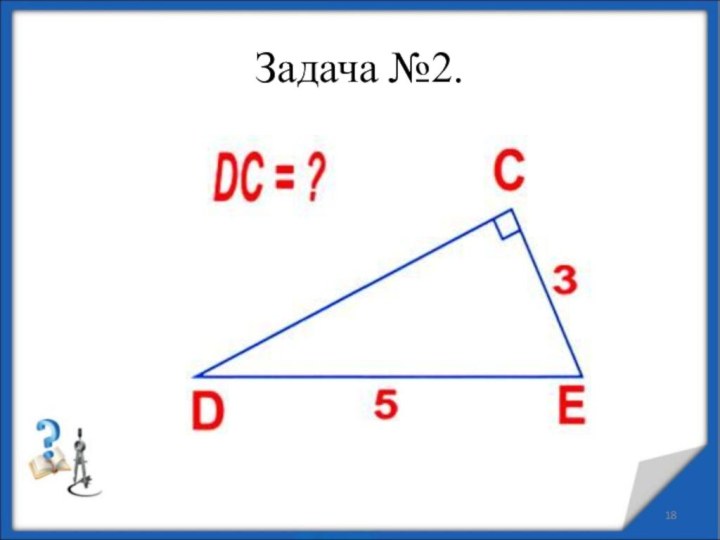
Слайд 19
Решение задачи №2
DCE − прямоугольный
с
гипотенузой DE
По теореме Пифагора:
DE2 = DС2 + CE2,
DC2
= DE2 − CE2,DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
Слайд 20
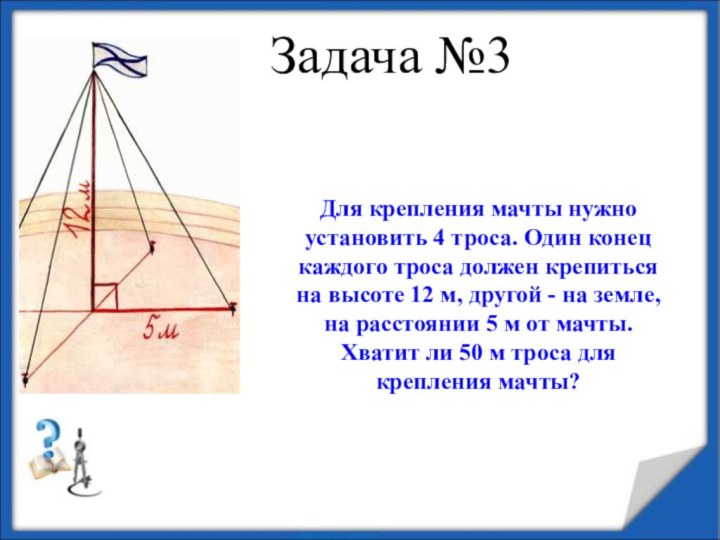
Задача №3
Для крепления мачты нужно установить 4 троса.
Один конец каждого троса должен крепиться на высоте 12
м, другой - на земле, на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?
Слайд 21
Итог урока
1. Возможно было решение задач данного
типа без знания теоремы Пифагора? Почему?
2. В чем суть
теоремы Пифагора?3. О чем надо помнить, применяя теорему Пифагора?