- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок математики в 11 классе по теме Двугранный угол. Трехгранный и многогранный углы
Содержание
- 2. Взаимное расположение прямых в пространствеа)аba
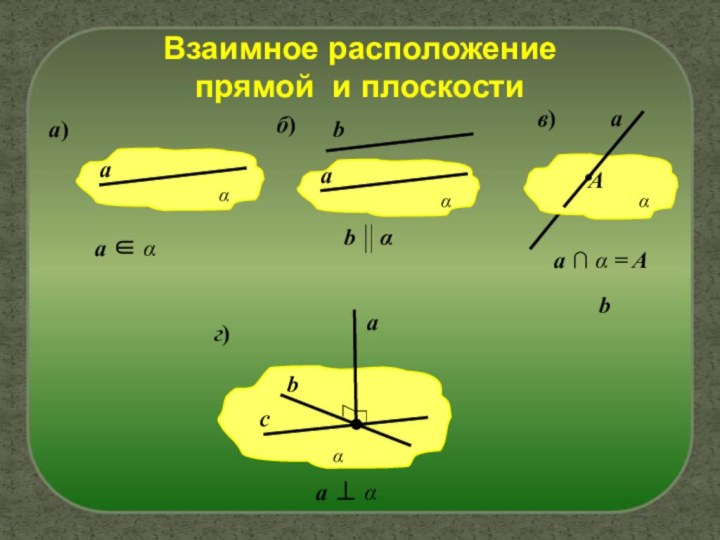
- 3. Взаимное расположение прямой и плоскостиа)bb αbб)a ⊥ αв)аa ∩ α = Aг)cαbαаa ∈ ααааαA
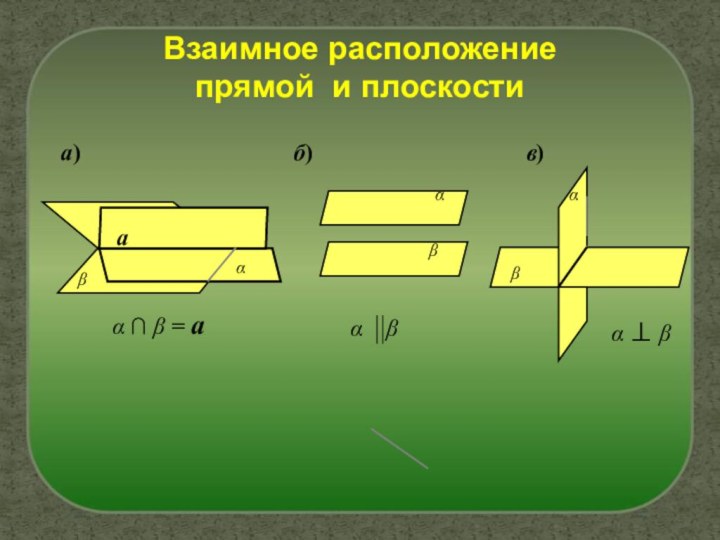
- 4. Взаимное расположение прямой и плоскостиа)α βб)α ⊥ βв)αаβα ∩ β = aαβαβ
- 5. Двугранным углом называется фигура, образованная двумя полуплоскостями
- 6. Линейным углом двугранного угла называется пересечение двугранного
- 7. Мера двугранного угла считается равной мере соответствующего
- 8. Величина двугранного угла находится в пределах
- 9. Алгоритм:γβCαПостроение линейного угла1. На ребре угла выбрать
- 10. SТрёхгранным углом (abc) называется фигура, составленная
- 11. AA1BCDB1C1D1Найти двугранный угол между:а) плоскостями ABB1A1 и
- 12. Задача № 1.Дано: Двугранный угол равен αγβAА∈γ,
- 13. Скачать презентацию
- 14. Похожие презентации
Взаимное расположение прямых в пространствеа)аba bаbб)a ⊥ bв)аbAa ∩ b = Aг)аαba ∩ b = ∅


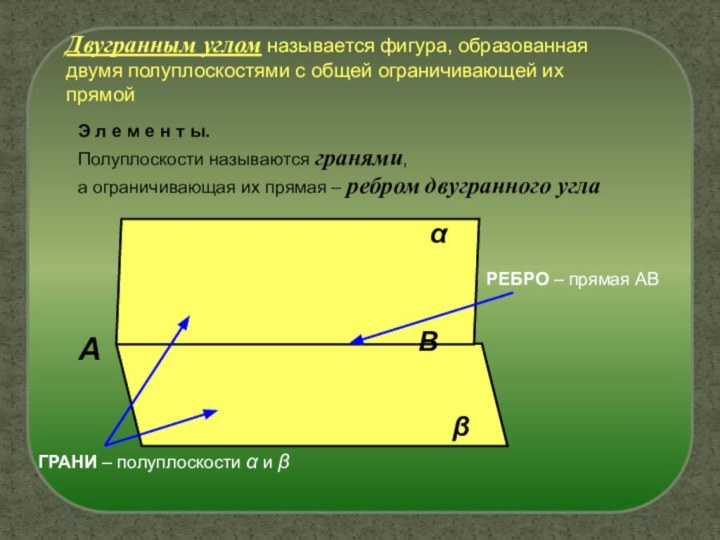






Слайд 5 Двугранным углом называется фигура, образованная двумя полуплоскостями с
общей ограничивающей их прямой
ГРАНИ – полуплоскости α и β
Э
л е м е н т ы.
Полуплоскости называются гранями,
а ограничивающая их прямая – ребром двугранного углаA
В
РЕБРО – прямая АВ
α
β
Слайд 6 Линейным углом двугранного угла называется пересечение двугранного угла
и плоскости, перпендикулярной его ребру
A
В
α
β
АВ – ребро;
α и β - грани a
b
a ∈ α, a ⊥ AB
b ∈ β, b⊥ AB
O
a ∩ b = O
∠(a , b) – линейный угол
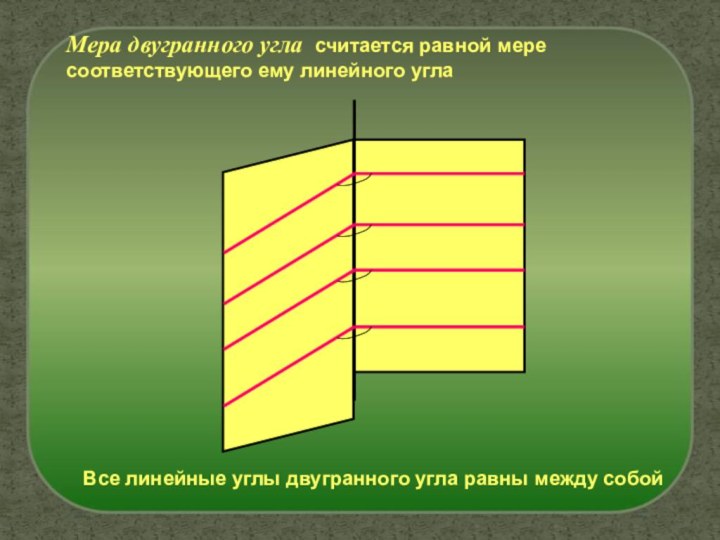
Слайд 7 Мера двугранного угла считается равной мере соответствующего ему
линейного угла
Все линейные углы двугранного угла равны между собой
Слайд 8 Величина двугранного угла находится в пределах от 0°
до 180°
α
α - острый угол
α
α = 90°
α
α - тупой
угол
Слайд 9
Алгоритм:
γ
β
C
α
Построение линейного угла
1. На ребре угла выбрать точку
2.
Провести в гранях через неё полупрямые,
перпендикулярные ребру.
Слайд 10
S
Трёхгранным углом (abc) называется фигура, составленная из
трех плоских углов (ab), (bc), (ac)
a
b
c
∠(ab), ∠(bc), ∠(ac) –
грани трёхгранного углаa, b и c – рёбра
S - вершина
Слайд 11
A
A1
B
C
D
B1
C1
D1
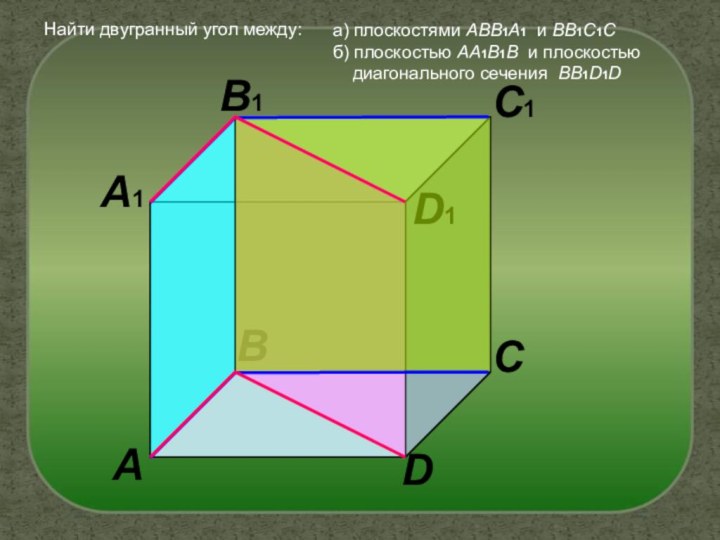
Найти двугранный угол между:
а) плоскостями ABB1A1 и BB1C1C
б)
плоскостью AA1B1B и плоскостью
диагонального сечения BB1D1D
Слайд 12
Задача № 1.
Дано: Двугранный угол равен α
γ
β
A
А∈γ,
В∈β
B
A1
B1
АА1 ⊥ n, ВВ1 ⊥ n,
n
АА1 = а,
ВВ1 = b, А1В1 = с
Найти: АВ
Решение: 1) строим A1C BB1
BC A1B1
С
α
a
b
c
2) A1B1BC - параллелограмм
⇓
A1C = BB1 = b
3) A1B1 ⊥ (АА1С) ⇒ BC ⊥ (АА1С)
⇓
ΔABС - прямоугольный (∠C = 90°)
4)
CB = A1B1 = c
6)
7)
5) ∠AA1С = α – линейный угол двугранного угла