- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Бриллианты элементарной геометрии
Содержание
- 2. Вопросы для повторенияТеорема косинусовПодобие треугольниковВписанный уголСвойство вписанных углов опирающихся на одну и туже дугу.Вписанный многоугольникФормулы приведения
- 3. Новые термины ЧЕВИАНА - отрезок
- 4. Теорема МЕНЕЛАЯКРАRНQNВС
- 5. Теорема ПаППАТеорема Паппа — это классическая теорема
- 6. Теоремы БрахмагуптаДан произвольный 4-х угольник около которого
- 8. Теорема ПтолемеяПусть даны 4 точки на окружностиТогда
- 9. Треугольники НаполеонаДан На сторонах произвольного треугольника
- 10. Теорема СТЮАРТААВnсlаmСД Дан треугольник со сторонами а,
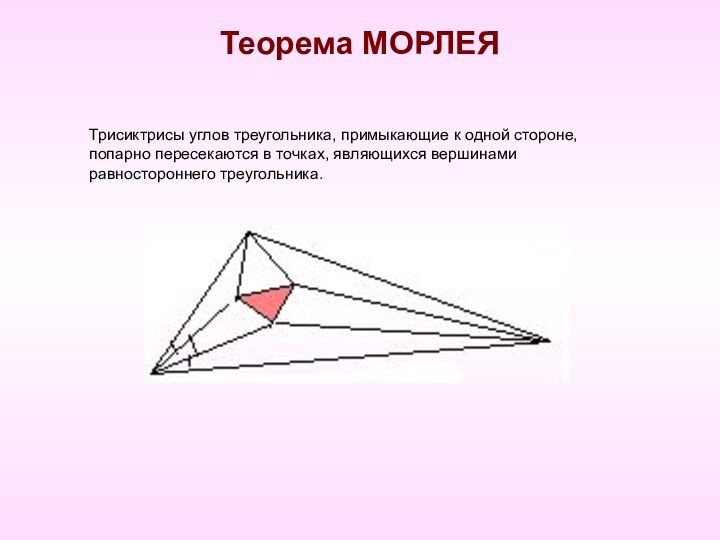
- 11. Теорема МОРЛЕЯТрисиктрисы углов треугольника, примыкающие к одной стороне, попарно пересекаются в точках, являющихся вершинами равностороннего треугольника.
- 12. ЗадачаРассадите 10 деревьев в десяти рядах, так чтобы в каждом ряду былоПо 3 дерева.
- 13. Домашнее заданиеRRQPАВС
- 16. Скачать презентацию
- 17. Похожие презентации
Вопросы для повторенияТеорема косинусовПодобие треугольниковВписанный уголСвойство вписанных углов опирающихся на одну и туже дугу.Вписанный многоугольникФормулы приведения















Слайд 2
Вопросы для повторения
Теорема косинусов
Подобие треугольников
Вписанный угол
Свойство вписанных углов
опирающихся на одну и туже дугу.
Слайд 3
Новые термины
ЧЕВИАНА - отрезок соединяющий
вершину треугольника с произвольной точкой противоположной стороны.
ТРИСЕКТРИСА - прямые
проходящие через вершину угла и делящие его на три равные части.
Слайд 5
Теорема ПаППА
Теорема Паппа — это классическая теорема проективной
геометрии — это классическая теорема проективной геометрии. Она является
частным случаем теоремы Паскаля. Теоремы можно сформулировать следующим образом:Пусть A, B, C — три точки на одной прямой, а A' , B' , C' — на другой. Пусть три прямые АВ' , BC' , CA' пересекают прямые A'B, B'C, C'A,
соответственно в точках X, Y и Z.
Тогда X, Y и Z лежат на одной прямой.
Слайд 6
Теоремы Брахмагупта
Дан произвольный 4-х угольник около которого можно
описать окружность.
Пусть длины его сторон a, b, c, d.
Тогда площадьЕго будет вычисляться по формуле
S=√(p-a) (p-b) (p-c) (p-d)
Если четырехугольник таков, что в него можно и вписать и описaть около
Него окружность, то его площадь может быть вычислена по формуле
S=√a b c d
Слайд 7
Теорема ЧЕВЫ
А
В
С
Р
Q
R
Дан произвольный треугольник. Внутри его
берется произвольная точка.Проводим чевианы.( чевиана- любой отрезок
Соединяющий точку стороны с вершиной угла)
Тогда: AP х ВQ х CR = BP х CQ х AR
Слайд 8
Теорема Птолемея
Пусть даны 4 точки на окружности
Тогда всегда
выполняется соотношение:
АВ х СД + АД х ВС =
АС х ВДСумма длин произведений противоположных сторон произвольного
4-х угольника около которого можно описать окружность, равна
Произведению диагоналей.
С
Д
В
А
К
Слайд 9
Треугольники Наполеона
Дан
На сторонах произвольного треугольника АВС
внешним образом построены как на основаниях равносторонние треугольники. Доказать,
что центры этих треугольников также являются вершинами равностороннего треугольника. .
Р
А
В
С
Р
А
В
м
С
К