не жили в такой геометрический период. Все вокруг -
геометрия»Ле Корбюдзе
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

















Ле Корбюдзе
провести из вершин многоугольника параллельные прямые
отложить на них равные отрезки
h
а1
а2
аn
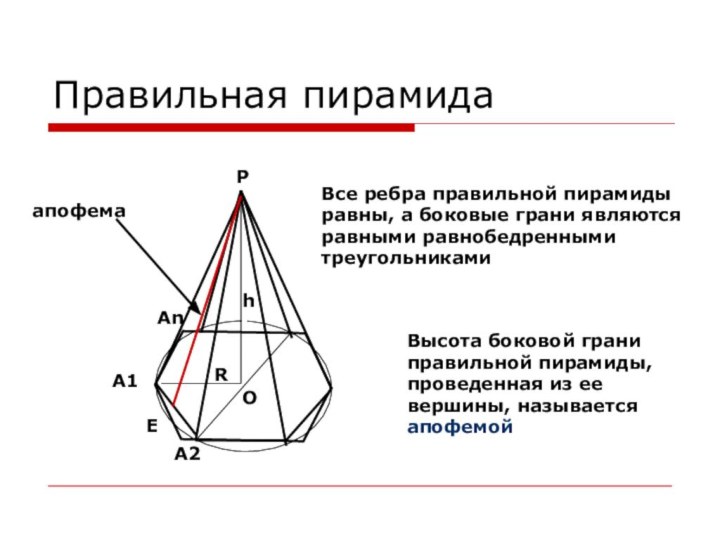
апофема