- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Определение подобных треугольников
Содержание
- 2. Что общего на этих рисунках?
- 3. 10. 05. 18.Классная работаОпределение подобных треугольников
- 4. Определение Подобные фигуры - это фигуры, имеющие одинаковую форму, но различные размеры.
- 5. НапримерПодобны две фотографии, отпечатанные с одного негатива, но с разными увеличениями.
- 6. НапримерПодобны архитектурное сооружение и его макет.
- 7. НапримерПодобны животное и его игрушечная фигурка .
- 8. Подобны любые два круга и любые два правильных многоугольника с одинаковым числом сторон.
- 9. Из этих примеров можно увидеть, что соответствующие
- 10. Так, на коробках игрушечных моделей самолётов указано,
- 11. ОпределениеДва треугольника называются подобными, если стороны одного
- 12. Подробнее: два треугольника подобны, если можно так
- 13. Если эти отношения обозначить через к, то
- 14. Из подобия двух треугольников вытекают как равенства
- 15. Рассматривая два подобных треугольника, мы
- 16. Если треугольник А1В1С1 подобен треугольнику АВС
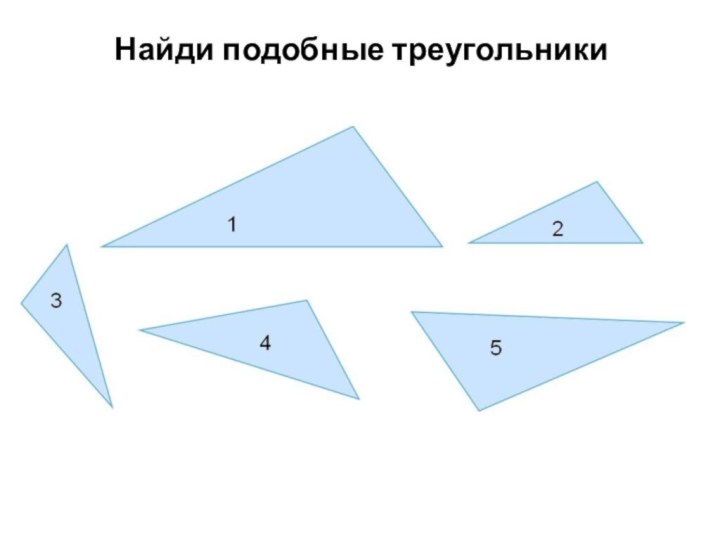
- 17. Найди подобные треугольники
- 18. Подобными называются треугольники, у которых соответствующие стороны
- 19. Если к = 1, то треугольники равны.
- 20. Вопросы для самоконтроля Какие фигуры называются подобными?Какие
- 21. Дополняем теорию№ 9.1; № 9.2; № 9.3
- 22. № 9.1Дано: ΔАВС, ∠С = 90° и
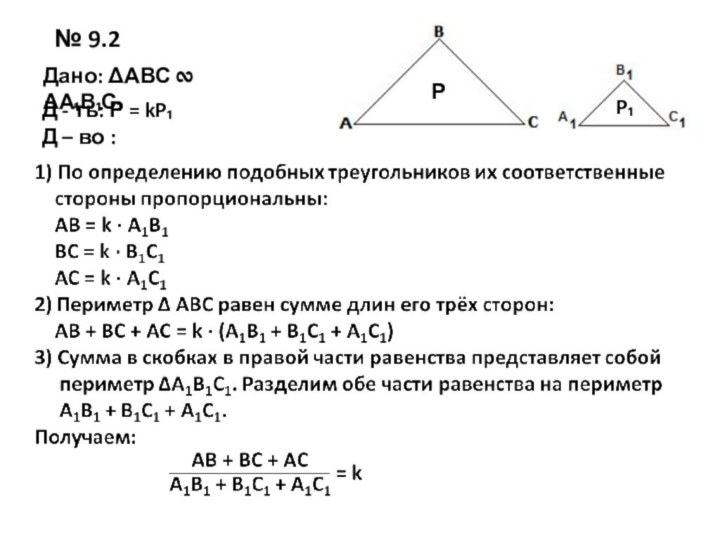
- 23. № 9.2Дано: ΔАВС ∾ ΔА₁В₁С₁Д - ть: Р = kP₁ Д – во :РP₁
- 24. № 9.2(а)Дано: ΔАВС и ΔА₁В₁С₁ - равнобедренные,
- 25. № 9.2(б)Дано: ΔАВС и ΔА₁В₁С₁ - равнобедренные,
- 26. № 9.8Hha₁b₁Ha₁b₁
- 27. Скачать презентацию
- 28. Похожие презентации
Что общего на этих рисунках?







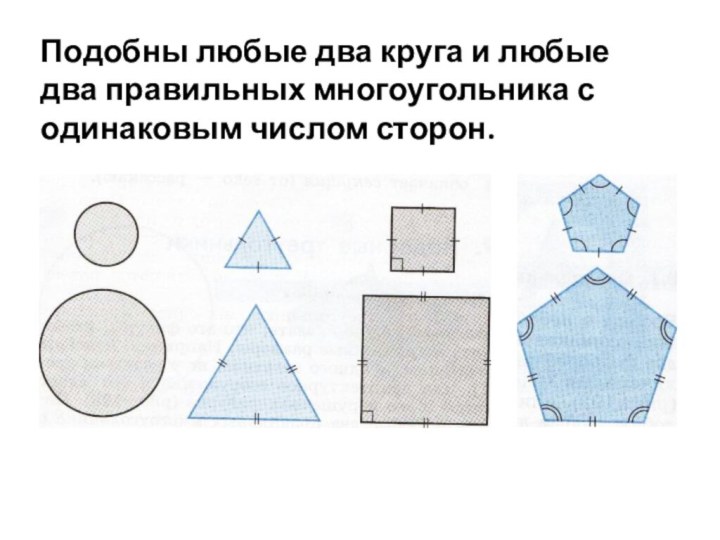










Слайд 9 Из этих примеров можно увидеть, что соответствующие линейные
размеры одной фигуры, подобной некоторой другой фигуре, в одно
и то же число раз меньше или больше линейных размеров другой фигуры.Слайд 10 Так, на коробках игрушечных моделей самолётов указано, во
сколько раз их детали меньше соответствующих деталей настоящих самолётов.
Поэтому все размеры одной из двух подобных фигур получают, умножая на некоторое число соответствующие размеры другой из них.
Слайд 11
Определение
Два треугольника называются подобными, если стороны одного из
них получаются из сторон другого умножением на некоторый множитель,
т. е. стороны одного треугольника пропорциональны сторонам другого треугольника.Подобными называются треугольники, у которых соответствующие стороны пропорциональны.
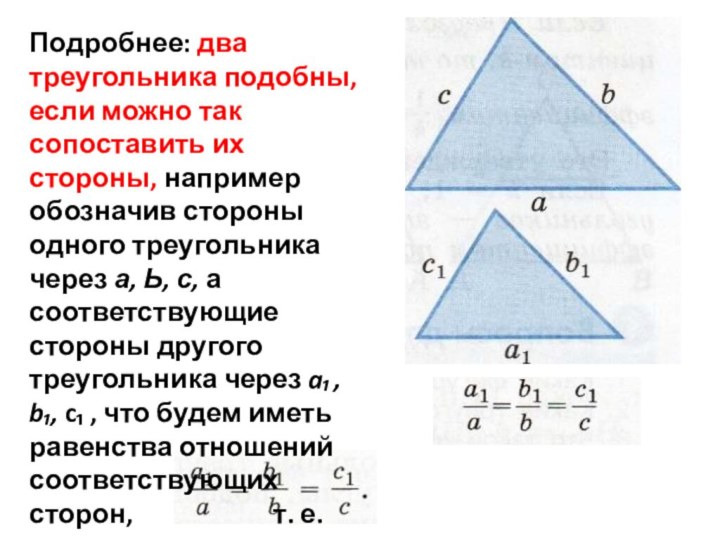
Слайд 12 Подробнее: два треугольника подобны, если можно так сопоставить
их стороны, например обозначив стороны одного треугольника через а,
Ь, с, а соответствующие стороны другого треугольника через a₁ , b₁, c₁ , что будем иметь равенства отношений соответствующих сторон, т. е. равенстваСлайд 13 Если эти отношения обозначить через к, то из
равенств (1) получаем, что
(1)
Ясно, что верно и обратное
утверждение: из равенств (2) следуют равенства (1). Итак, равенства (1) и (2) равносильны. Положительное число k называется коэффициентом подобия.(2)
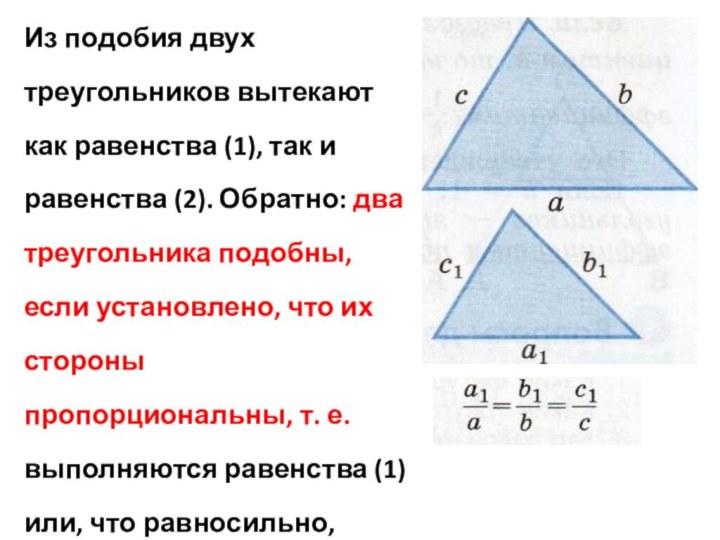
Слайд 14 Из подобия двух треугольников вытекают как равенства (1),
так и равенства (2). Обратно: два треугольника подобны, если
установлено, что их стороны пропорциональны, т. е. выполняются равенства (1) или, что равносильно, равенства (2).Слайд 15 Рассматривая два подобных треугольника, мы считаем
выбранными введённые здесь обозначения их сторон, а вершины треугольников,
лежащие против этих сторон, обозначаем, как обычно, через А, В, С, А₁, В₁, С₁.Итак, говорят, что треугольник А1В1С1 подобен треугольнику АВС с коэффициентом k, если выполняются равенства (2).
В этом случае пишут: ∆А1В1С1 ∾ ∆АВС.
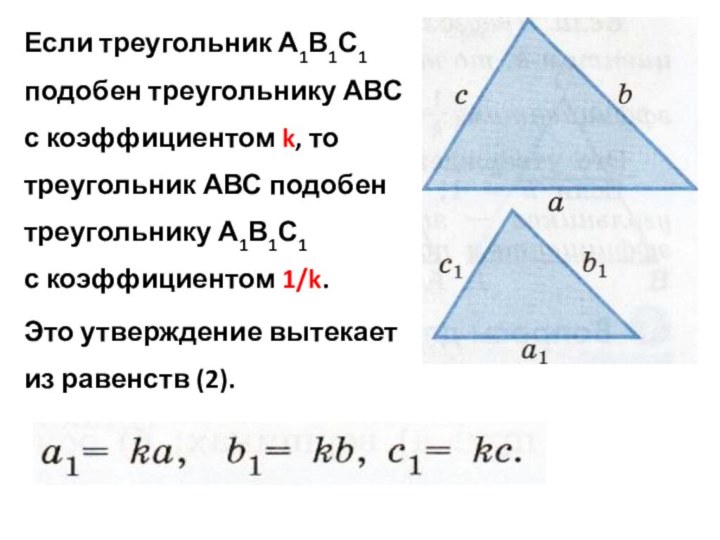
Слайд 16 Если треугольник А1В1С1 подобен треугольнику АВС
с коэффициентом
k, то треугольник АВС подобен треугольнику А1В1С1 с коэффициентом 1/k.Это утверждение вытекает из равенств (2).
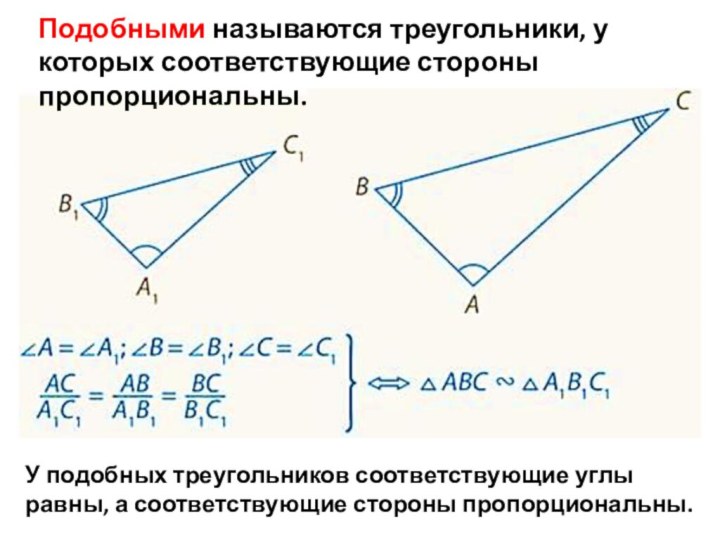
Слайд 18 Подобными называются треугольники, у которых соответствующие стороны пропорциональны.
У подобных треугольников соответствующие углы равны, а соответствующие стороны
пропорциональны.Слайд 19 Если к = 1, то треугольники равны. Поэтому
равенство треугольников — это частный случай подобия треугольников (с
коэффициентом подобия, равным единице).
Слайд 20
Вопросы для самоконтроля
Какие фигуры называются подобными?
Какие треугольники называются
подобными?
Что такое коэффициент подобия?
Верно ли, что равные треугольники подобны?
Равны ли подобные треугольники?
Слайд 22
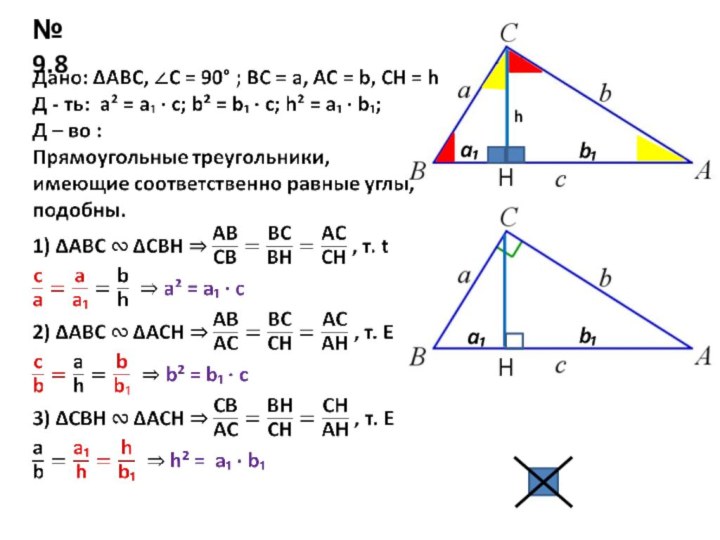
№ 9.1
Дано: ΔАВС, ∠С = 90° и ΔА₁В₁С₁,
∠С₁ = 90°;
∠А
= ∠А₁ Д - ть: ΔАВС ∾ ΔА₁В₁С₁;
Д – во :
1) Т. к сумма острых углов в прямоугольном треугольнике равна
90° , то ∠В = ∠В₁.
2) tg A = ВС : АС, tg A₁ = В₁С₁ : А₁С₁.
Т. к ∠А = ∠А₁ , то ВС : АС = В₁С₁ : А₁С₁.
Следовательно ВС : В₁С₁ = АС : А₁С₁
3) sin A = ВС : АB, sin A₁ = В₁С₁ : А₁B₁.
Т. к ∠А = ∠А₁ , то ВС : АB = В₁С₁ : А₁B₁.
Следовательно ВС : В₁С₁ = АB : А₁B₁.
4) АB : А₁B₁ =ВС : В₁С₁ = АС : А₁С₁ .
Следовательно ΔАВС ∾ ΔА₁В₁С₁.
Слайд 24
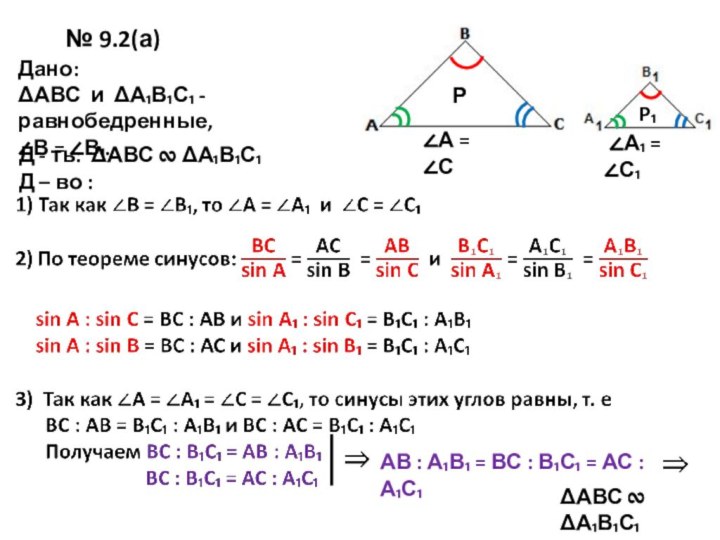
№ 9.2(а)
Дано:
ΔАВС и ΔА₁В₁С₁ - равнобедренные,
∠В
= ∠В₁.
Д - ть: ΔАВС ∾ ΔА₁В₁С₁
Д – во
:Р
P₁
АВ : А₁В₁ = ВС : В₁С₁ = АС : А₁С₁
ΔАВС ∾ ΔА₁В₁С₁
∠А = ∠С
∠А₁ = ∠С₁
Слайд 25
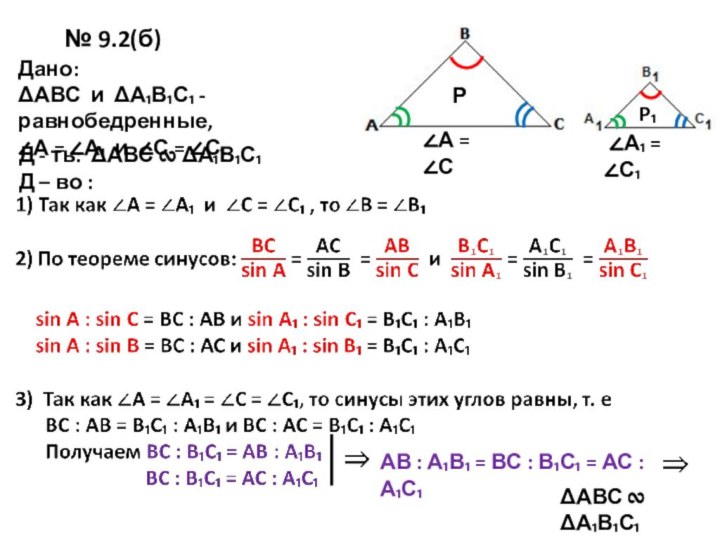
№ 9.2(б)
Дано:
ΔАВС и ΔА₁В₁С₁ - равнобедренные,
∠А
= ∠А₁ и ∠С = ∠С₁
Д - ть:
ΔАВС ∾ ΔА₁В₁С₁Д – во :
Р
P₁
АВ : А₁В₁ = ВС : В₁С₁ = АС : А₁С₁
ΔАВС ∾ ΔА₁В₁С₁
∠А = ∠С
∠А₁ = ∠С₁