- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Усеченный конус(11 класс)
Содержание
- 2. Усеченным конусом называется часть полного
- 3. Образующей усеченного конуса называется часть
- 4. Усеченный конус можно рассматривать как
- 5. Прямая, соединяющая центры оснований, называется
- 6. Боковая поверхность усеченного конуса. Площадь боковой поверхности
- 7. Доказательство: Боковую поверхность усеченного конуса будем
- 8. Доказательство: Впишем в конус правильную пирамиду. Ее боковая поверхность состоит из трапеций.
- 9. Площадь боковой поверхности усеченного конуса
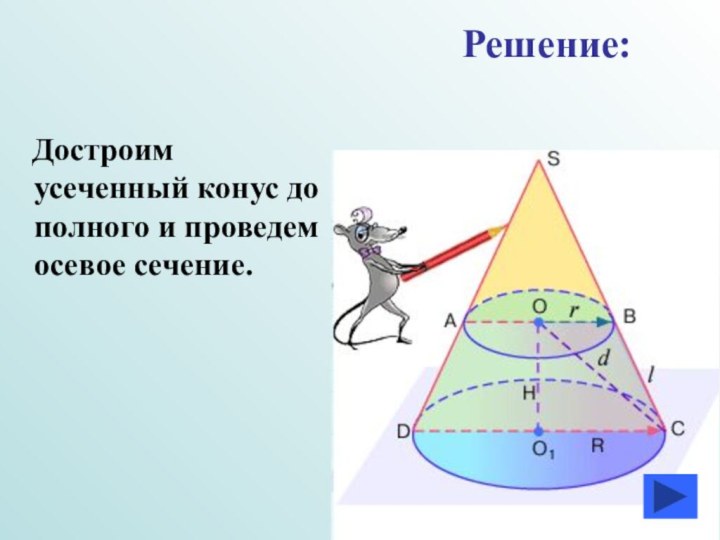
- 10. Достроим усеченный конус до полного и проведем осевое сечение.Решение:
- 11. Формула объема усеченного конуса.Объем усеченного конуса равен
- 12. Поместим на верхнем основании усеченного
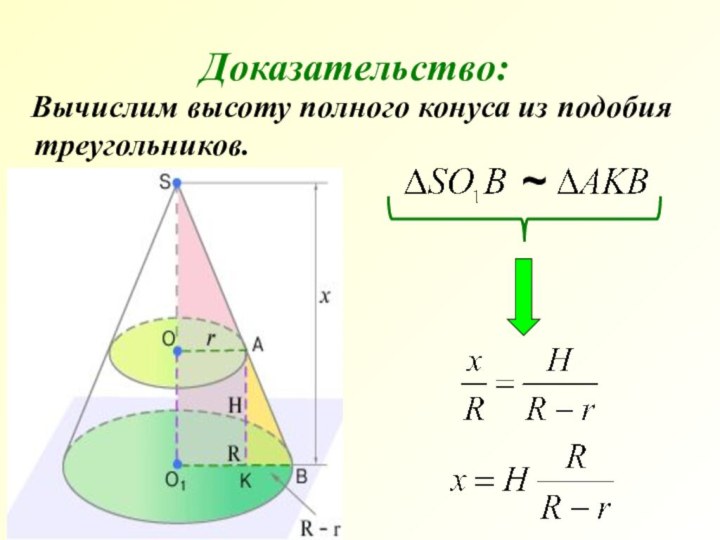
- 13. Вычислим высоту полного конуса из подобия треугольников.Доказательство:~
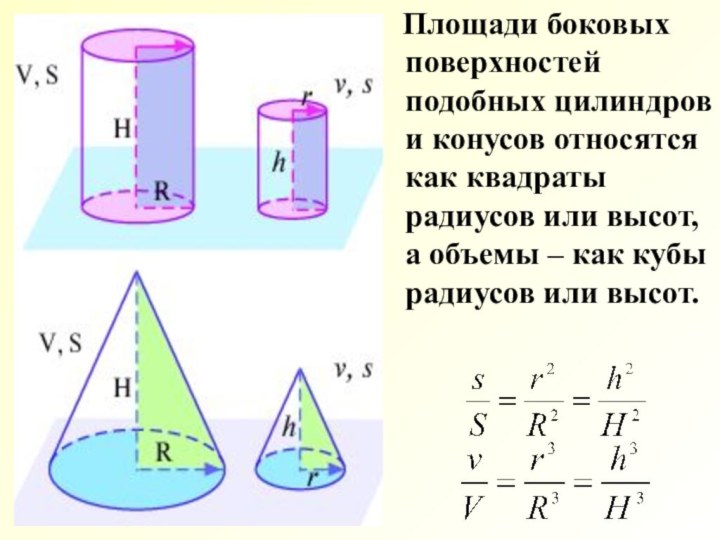
- 14. Объемы полного и дополнительного конусов относятся как кубы радиусов оснований.Доказательство:~
- 15. Вычтем из объема большого конуса объем малого конуса.Доказательство:
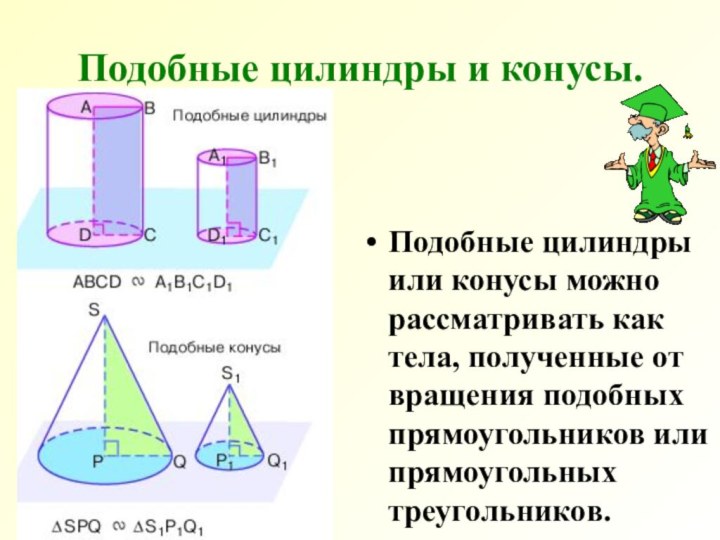
- 16. Подобные цилиндры и конусы.Подобные цилиндры или конусы
- 17. Сечение, параллельное основанию конуса, отсекает от него малый конус, подобный большому.
- 18. Скачать презентацию
- 19. Похожие презентации
Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.


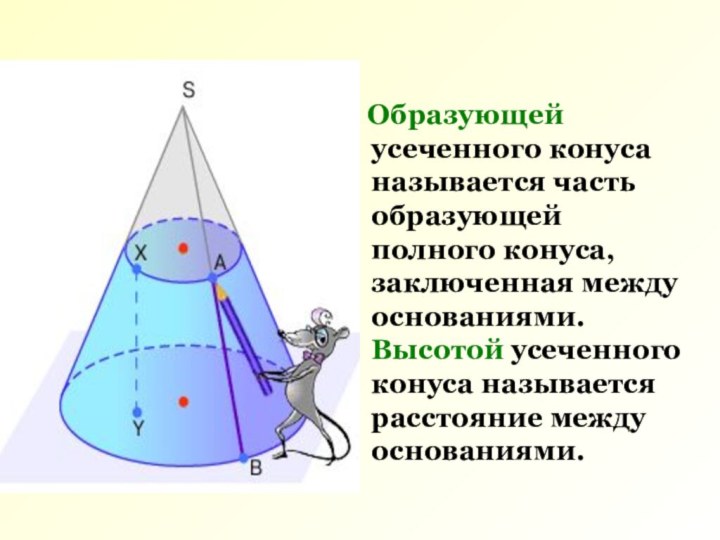





Слайд 3 Образующей усеченного конуса называется часть образующей
полного конуса, заключенная между основаниями. Высотой усеченного конуса называется
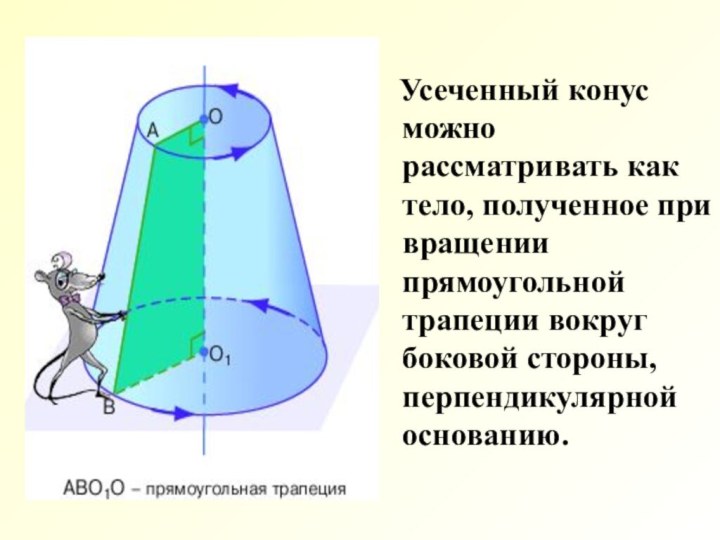
расстояние между основаниями.Слайд 4 Усеченный конус можно рассматривать как тело,
полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной
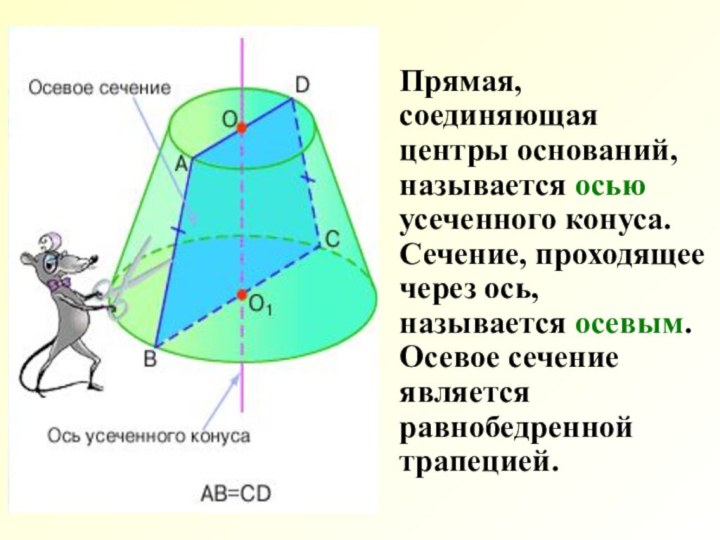
основанию.Слайд 5 Прямая, соединяющая центры оснований, называется осью
усеченного конуса. Сечение, проходящее через ось, называется осевым. Осевое
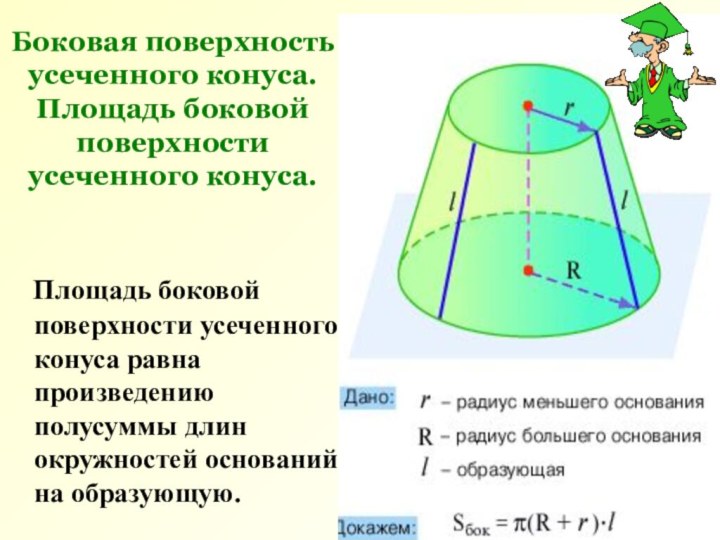
сечение является равнобедренной трапецией.Слайд 6 Боковая поверхность усеченного конуса. Площадь боковой поверхности усеченного
конуса.
Площадь боковой поверхности усеченного конуса равна произведению
полусуммы длин окружностей оснований на образующую.
Слайд 7
Доказательство:
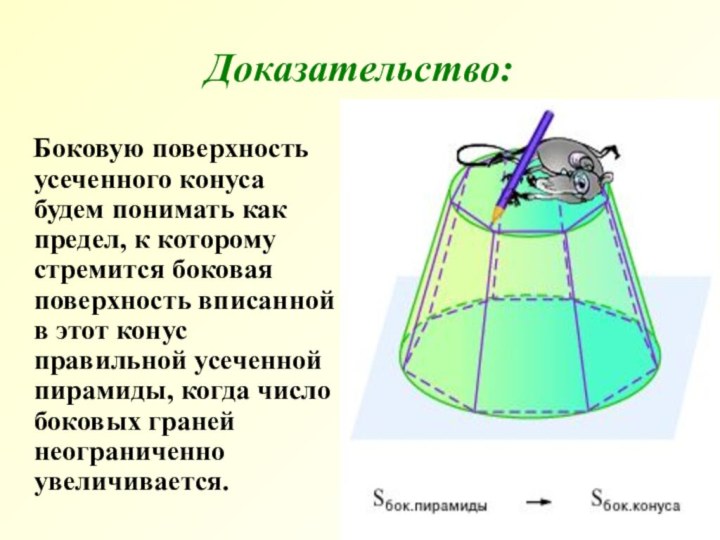
Боковую поверхность усеченного конуса будем понимать
как предел, к которому стремится боковая поверхность вписанной в
этот конус правильной усеченной пирамиды, когда число боковых граней неограниченно увеличивается.
Слайд 8
Доказательство:
Впишем в конус правильную пирамиду. Ее
боковая поверхность состоит из трапеций.
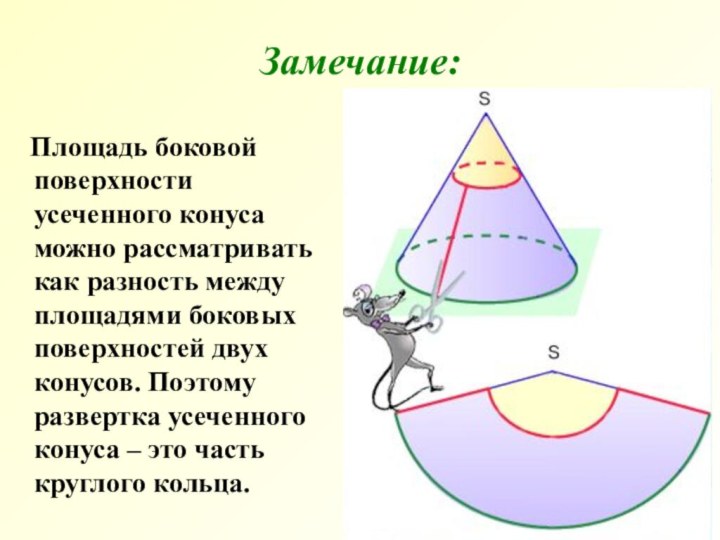
Слайд 9 Площадь боковой поверхности усеченного конуса можно
рассматривать как разность между площадями боковых поверхностей двух конусов.
Поэтому развертка усеченного конуса – это часть круглого кольца.Замечание:
Слайд 11
Формула объема усеченного конуса.
Объем усеченного конуса равен сумме
объемов трех конусов, имеющих одинаковую высоту с усеченным конусом,
а основаниями: один – нижнее основание этого конуса, другой – верхнее, а третий – круг, радиус которого есть среднее геометрическое между радиусами верхнего и нижнего оснований.
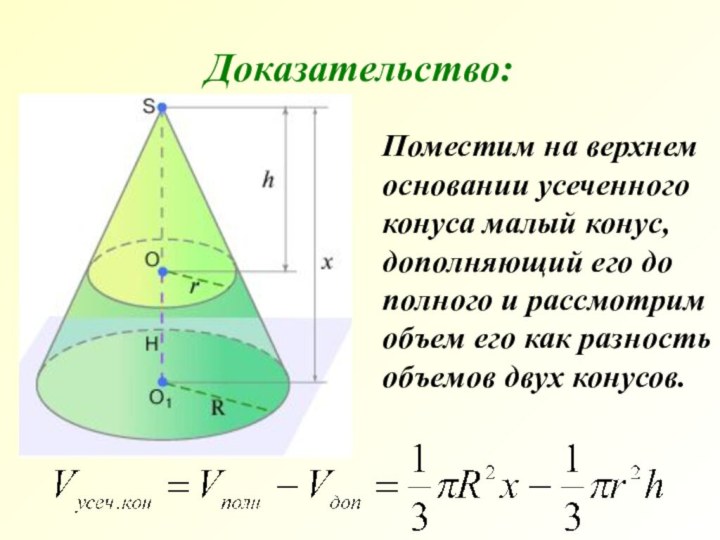
Слайд 12 Поместим на верхнем основании усеченного конуса
малый конус, дополняющий его до полного и рассмотрим объем
его как разность объемов двух конусов.Доказательство: