- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Элементы геометрии Лобачевского (7 класс)
Содержание
- 2. Геометрия оформилась в стройную математическую науку, имеющую
- 3. Евклид написал 13 книг
- 4. Постулаты ЕвклидаОтрезок прямой линии может быть прочерчен,
- 5. Пятый постулат, однако, не разделяет
- 6. В течение более двух тысяч
- 7. Великий русский учёный-геометр Н.И. Лобачевский
- 8. В основе этой геометрии лежат все аксиомы
- 9. перпендикуляр и наклонная к одной
- 10. Исходя из этих аксиом, принятых
- 11. Реальна ли геометрия Лобачевского? Чтобы ответить
- 12. Если нарисовать треугольник на листе,
- 13. Геодезическими линиями какой-нибудь поверхности обычно называют
- 14. Посмотрим, какая геометрия выполняется на сфере, если
- 15. Геодезическими линиями на сфере являются
- 16. Характерной особенностью этой геометрии сферы
- 17. Этот факт легко усматривается на чертеже
- 18. Итак, реальна ли геометрия Лобачевского? Да,
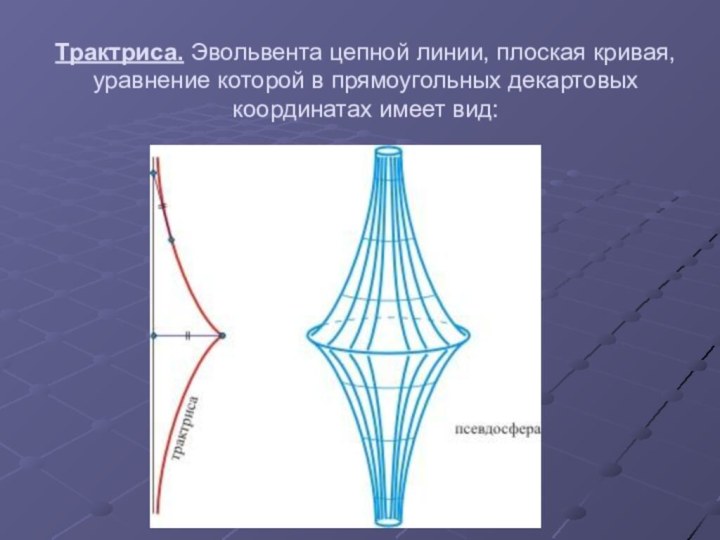
- 19. Трактриса. Эвольвента цепной линии, плоская кривая, уравнение которой в прямоугольных декартовых координатах имеет вид:
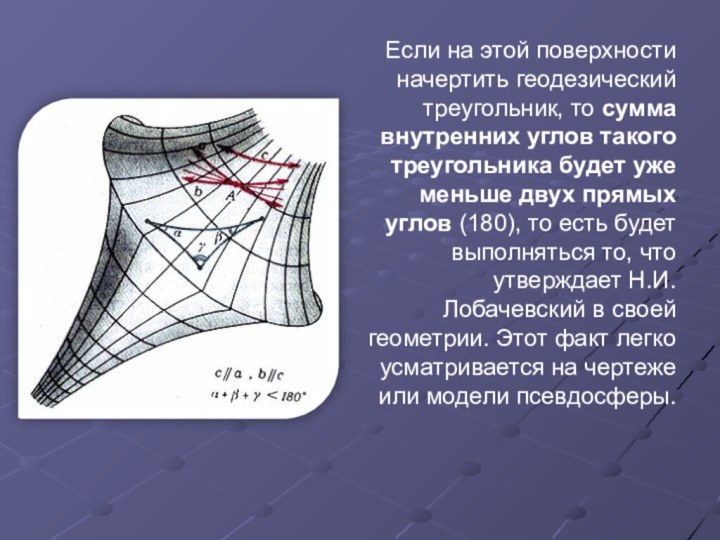
- 20. Если на этой поверхности начертить
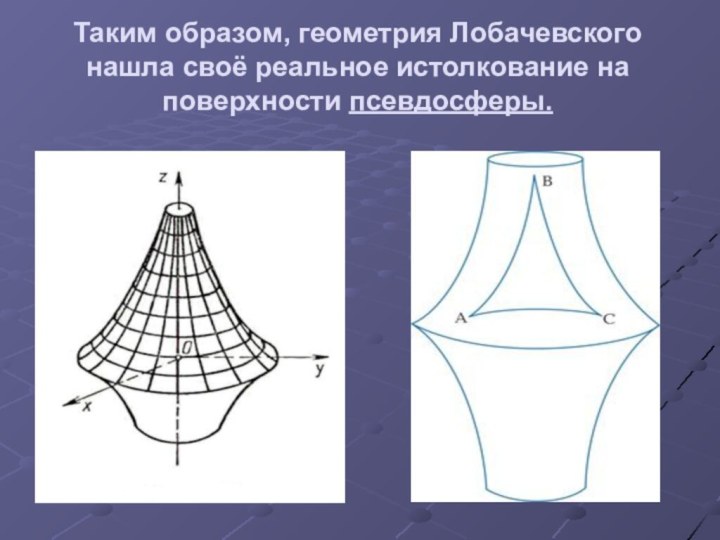
- 21. Таким образом, геометрия Лобачевского нашла своё реальное истолкование на поверхности псевдосферы.
- 22. Открытие геометрии Лобачевского составляет целую эпоху в
- 23. Геометрия Лобачевского нашла своё непосредственное приложение в
- 24. Спасибо за внимание!
- 25. Список использованных источников:А) печатныхГеометрия Лобачевского и элементы
- 26. Скачать презентацию
- 27. Похожие презентации
Геометрия оформилась в стройную математическую науку, имеющую прикладное значение, в III веке до н.э. в работах древнегреческого математика Евклида.























Слайд 3
Евклид написал
13 книг по
геометрии под общим названием «Начала», по ним в течение
ряда веков обучались геометрии. Даже в настоящее время в Англии изучение геометрии в школах ведётся по «Началам» Евклида.
Слайд 4
Постулаты Евклида
Отрезок прямой линии может быть прочерчен, если
соединить две точки.
(2) Любой отрезок прямой линии может быть
неопределенно долго продлён вдоль неё.(4) Все прямые углы конгруэнтны.
(2)
(3) Дан некоторый отрезок прямой линии. Окружность может быть построена, если иметь отрезок как радиус и одну точку на конце отрезка использовать как центр.
Слайд 5 Пятый постулат, однако, не разделяет изящества
братьев:
(5) Если проведены две линии, которые пересекаются
третьей линией таким образом, что сумма внутренних углов на данной стороне меньше чем два прямых угла, тогда эти две прямых линии неизбежно должны пересечься друг с другом на этой стороне, если их продолжить неопределенно долго.Слайд 6 В течение более двух тысяч лет
учёные всех стран считали, что иной геометрии, кроме Евклидовой,
быть не может. С целью доказать это они старались на основе прочих аксиом доказать пятый постулат Евклида:«Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой».
Но все попытки доказать данный постулат не принесли успеха.
Слайд 7 Великий русский учёный-геометр Н.И. Лобачевский в
1826 году установил недоказуемость аксиомы о параллельных прямых тем,
что построил неевклидову геометрию, геометрию Лобачевского.Слайд 8 В основе этой геометрии лежат все аксиомы геометрии
Евклида, за исключением пятого постулата, который Н.И.Лобачевский сформулировал так:
«Через точку, взятую вне прямой на плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данную».
Слайд 9
перпендикуляр и наклонная к одной и
той же прямой, расположенные в одной плоскости, могут не
пересекаться;сумма всех внутренних углов треугольника меняется от треугольника к треугольнику (зависит от его сторон), но всегда меньше 180º;
Исходя из этих аксиом, принятых геометрией Лобачевского, в качестве теорем доказывается, что:
Слайд 10 Исходя из этих аксиом, принятых геометрией
Лобачевского, в качестве теорем доказывается, что:
сумма всех внутренних углов
всякого выпуклого четырёхугольника меньше 360º. Отсюда как следствие вытекает: прямоугольника не существует;геометрическое место точек, равноудалённых от данной прямой и расположенных по одну сторону от неё на плоскости, не может быть прямой (а есть всегда кривая линия).
Слайд 11
Реальна ли геометрия Лобачевского?
Чтобы ответить на
это надо, прежде всего, ответить на вопрос, что нужно
понимать под точкой, прямой и плоскостью.ТОЧКА - это ШАР радиуса r.
ПРЯМАЯ - это бесконечный круговой ЦИЛИНДР радиуса r.
ПЛОСКОСТЬ - это ПЛОСКОПАРАЛЛЕЛЬНАЯ ПЛАСТИНКА толщиной 2r.
Слайд 12 Если нарисовать треугольник на листе, а
затем свернуть лист в цилиндр, то стороны треугольника становятся
кривыми линиями.Линии на поверхности цилиндра, которые при развёртывании цилиндра на плоскость переходят в прямые, называются геодезическими линиями цилиндра.
Слайд 13 Геодезическими линиями какой-нибудь поверхности обычно называют линии
кратчайшего расстояния между двумя точками поверхности. Если за «точки»
принять точки цилиндра, а за «прямые» - геодезические линии цилиндра, тогда на цилиндре будет выполняться евклидова планиметрия.Слайд 14 Посмотрим, какая геометрия выполняется на сфере, если за
«точки» принять точки этой сферы, а за «прямые» -
её геодезические линии (сфера без растяжения, путём одного только изгибания, на плоскость не развёртывается и геодезические линии её не могут, как у цилиндра переходить в прямые).
Слайд 15 Геодезическими линиями на сфере являются дуги
больших кругов, они имеют общий центр в центре сферы
и попарно пересекаются. Поэтому на сфере нет параллельных «прямых». Следовательно, через «точку», взятую вне «прямой», на сфере нельзя провести ни одной «прямой», параллельной данной.Слайд 16 Характерной особенностью этой геометрии сферы является
то, что сумма внутренних углов треугольника больше двух прямых
углов.
Слайд 17
Этот факт легко усматривается
на чертеже или модели.
Геометрия сферы есть простейшая модель так называемой
неевклидовой геометрии Римана.
Слайд 18
Итак, реальна ли геометрия Лобачевского?
Да, реальна,
поскольку она выполняется на реальных поверхностях. Оказывается геометрия Лобачевского
(планиметрия) выполняется на поверхности псевдосферы (поверхность вращения трактрисы вокруг оси).Слайд 19 Трактриса. Эвольвента цепной линии, плоская кривая, уравнение которой
в прямоугольных декартовых координатах имеет вид:
Слайд 20 Если на этой поверхности начертить геодезический
треугольник, то сумма внутренних углов такого треугольника будет уже
меньше двух прямых углов (180), то есть будет выполняться то, что утверждает Н.И.Лобачевский в своей геометрии. Этот факт легко усматривается на чертеже или модели псевдосферы.Слайд 21 Таким образом, геометрия Лобачевского нашла своё реальное истолкование
на поверхности псевдосферы.
Слайд 22 Открытие геометрии Лобачевского составляет целую эпоху в науке.
Идеи Лобачевского находят широкое применение в современной физике. Например,
по замыслу Н.И.Лобачевского строятся современные теории механики мирового пространства.Слайд 23 Геометрия Лобачевского нашла своё непосредственное приложение в теории
функций комплексного переменного. Ещё сам Лобачевский использовал свою геометрию
для вычисления определённых интегралов.Мы гордимся тем, что неевклидова геометрия открыта в России и что её открыл русский учёный Н.И.Лобачевский.
Слайд 25
Список использованных источников:
А) печатных
Геометрия Лобачевского и элементы оснований
геометрии. (Пособие для учителей средней школы) Автор: Кутузов Б.В.
Издательство: Государственное учебно-педагогическое издание Министерства Просвещения РСФСР Год изд.: 1950Б) изображения
Портрет Лобачевского
http:///datas/istorija/Russkaja-kultura-v-XIX-veke/0007-007-Lobachevskij-Nikolaj-Ivanovich.jpg
Евклид
http://gym1505.ru/sites/default/files/styles/inner-page/public/blogs/euklid-von-alexandria_1.jpg?itok=__2HZOMR
Сфера
http://topref.ru/main/images/95186/m16725c74.png
Псевдосфера
http://www.rithm-time.ru/issues/2007/30/PFR-3.jpg
Мальчик (анимация)
http://2.bp.blogspot.com/-JppMzJ8bsOc/Upl5Ux_uQ6I/AAAAAAAAAN0/N8RIdNv7oa8/s1600/mat.gif





























