- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Шар и сфера
Содержание
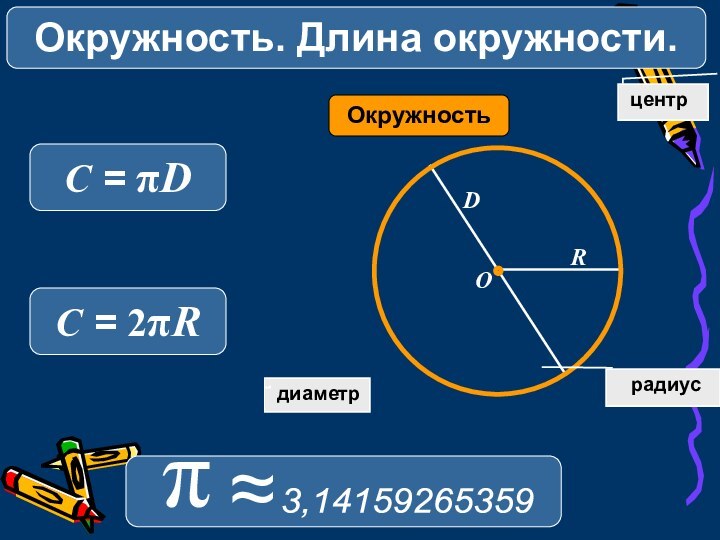
- 2. диаметрОкружностьКолесо центр RDO радиус3,14159265359 π≈Окружность. Длина окружности.C = πDC = 2πR
- 3. ПЛОЩАДЬ КРУГА ·(a · n) · hπR2Sкруга = πR2
- 4. Окружность при вращении вокруг любой из осей
- 5. По аналогии с окружностью объясните, что такое:
- 6. ШАР СФЕРА S = 4πR2
- 7. ШАР СФЕРА диаметррадиусЦентр шара (сферы)ГЕОМЕТРИЧЕСКИЙ РИСУНОК
- 8. Вычислительный центр.Ребята, вы все сейчас становитесь членами вычислительного центра.От вас требуется внимательность,сосредоточенность, активность, точность.
- 9. Задача 1.Найдите площадь поверхности шара радиусом 3м. Какой объем имеет такой шар?
- 10. Задача 2. Найдите радиус земного шара
- 11. Задача 3.На рынке был куплен арбуз массой:1)10
- 12. Из таблицы видно, что радиус арбуза больше
- 13. Скачать презентацию
- 14. Похожие презентации
диаметрОкружностьКолесо центр RDO радиус3,14159265359 π≈Окружность. Длина окружности.C = πDC = 2πR

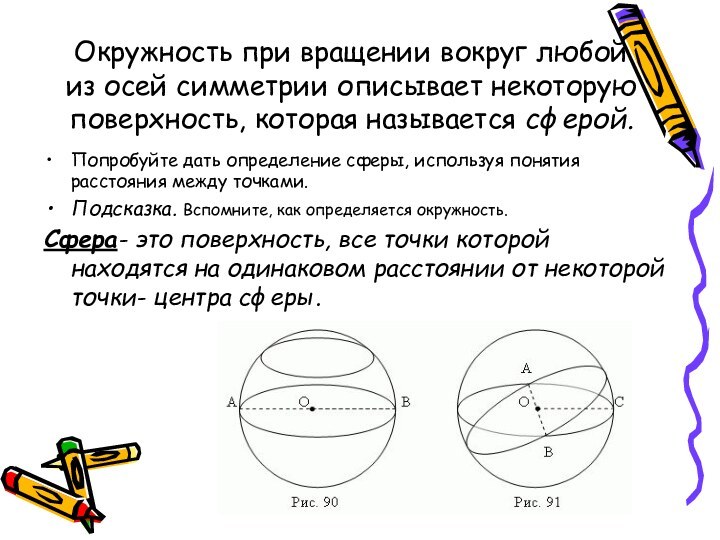









Слайд 4 Окружность при вращении вокруг любой из осей симметрии
описывает некоторую поверхность, которая называется сферой.
Попробуйте дать определение сферы,
используя понятия расстояния между точками.Подсказка. Вспомните, как определяется окружность.
Сфера- это поверхность, все точки которой находятся на одинаковом расстоянии от некоторой точки- центра сферы.
Слайд 5 По аналогии с окружностью объясните, что такое: а)радиус;
б)хорда; в)диаметр сферы.
Как окружность связана с кругом, так и
сфера связана с шаром; Шар-это часть пространства, ограниченная сферой.
У сферы и шара есть две главные формулы - формулы площади сферы и объема шара:
площадь сферы Sсферы=4πR2;
объем шара Vшара =4/3πR3.
С выводом этих формул вы познакомитесь только в старших классах, однако это не должно мешать вам использовать их уже сейчас.
Слайд 8
Вычислительный центр.
Ребята, вы все сейчас становитесь членами вычислительного
центра.
От вас требуется
внимательность,
сосредоточенность,
активность, точность.
Слайд 10 Задача 2. Найдите радиус земного шара и площадь поверхности
Земли.
(Радиус найдите с точностью до 100 км.)
Слайд 11
Задача 3.
На рынке был куплен арбуз массой:
1)10 кг;
б)16 кг.
Какие примерно у него радиус и площадь
поверхности?(Арбуз на 99% состоит из воды, 1 дм3 который имеет массу 1 кг)
Комментарий. Арбуз практически полностью состоит из воды, поэтому можно считать, что его масса 10 кг и, следовательно, объем 10 дм3.
Будем искать радиус шара объемом 10 дм3 :
10=4/3πR3≈4/3*3,14*R3 ≈4R3.
Найдем R из уравнения 10=4R3;
R3=2,5.
Подберем значение R с точностью до 1см.
Слайд 12 Из таблицы видно, что радиус арбуза больше 13см,
но меньше 14см. За приближенное значение радиуса можно взять
любое из этих чисел, например 13. По формуле площади сферы найдем S=4π∙132≈4∙3,14∙169 ≈2100(см2). Ответ: радиус арбуза 13 см, площадь его поверхности 2100 см2.Постарайтесь вспомнить эту задачу в конце летних каникул, когда встретитесь с арбузами ☺