- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Осевая и центральная симметрия( 8 класс)
Содержание
- 2. Теоретическая самостоятельная работаПроверка
- 3. Теоретическая самостоятельная работа
- 4. Проверочный тестПроверка
- 5. Ответы к тестуI вариант1 – в),2 –
- 6. Осевая и центральная симметрии
- 7. «Симметрия является той идеей, с помощью которой
- 8. В древности слово «СИММЕТРИЯ» употреблялось
- 9. Осевая симметрия Точки А и А1
- 10. Симметричность относительно прямой
- 11. У прямоугольника 2 оси симметрии
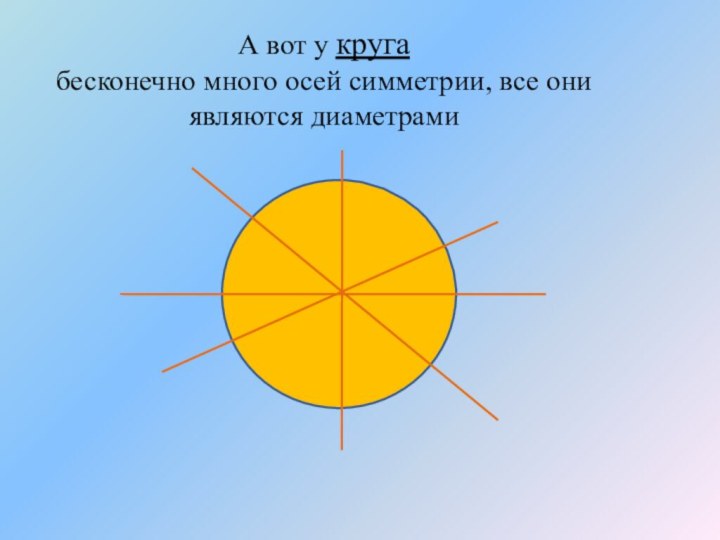
- 12. А вот у круга бесконечно много осей симметрии, все они являются диаметрами
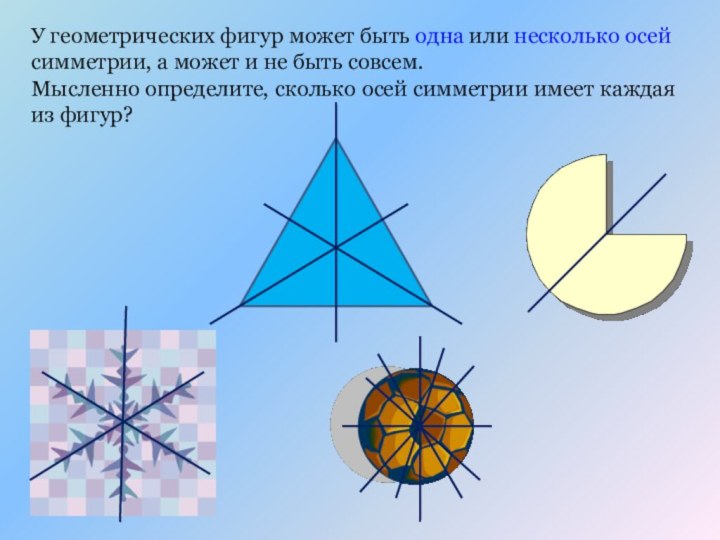
- 13. У геометрических фигур может быть одна или
- 14. У геометрических фигур может быть одна или
- 15. Центральная симметрия Точки А1 и А2 называются
- 16. Центральная симметрия А В СА1С1АВСОС1А1В1
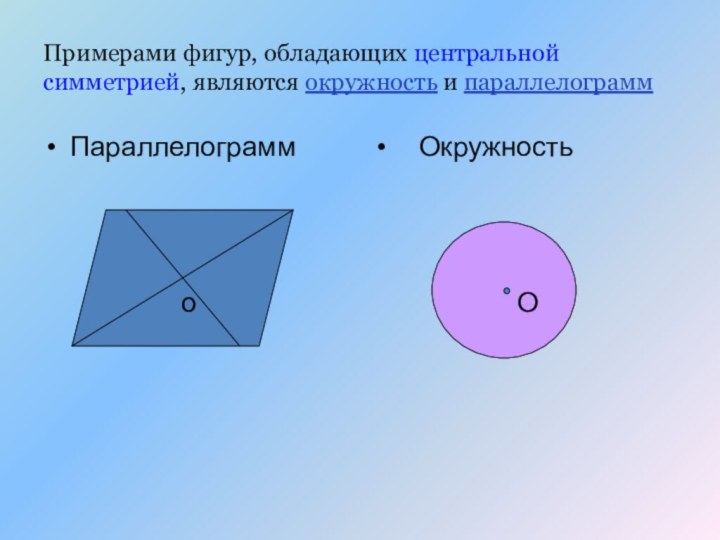
- 17. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограммПараллелограмм ОкружностьоО
- 18. Фигуры, обладающие центральной и осевой симметриейОВАLNDСФигура называется
- 19. ОСЕВАЯ СИММЕТРИЯ
- 28. СИММЕТРИЯ В ПРИРОДЕ Самым ярким примером красоты
- 29. СИММЕТРИЯ В АРХИТЕКТУРЕ Примером современных зданий, построенных
- 30. СИММЕТРИЯ В БЫТУ Издревле люди стремились украсить
- 31. СИММЕТРИЯ В ИССКУСТВЕ Симметричная композиция легко воспринимается
- 32. Природа говорит языком математики: буквы этого языка - круги, треугольники и иные математические фигуры. Галилей.
- 33. Скачать презентацию
- 34. Похожие презентации
Теоретическая самостоятельная работаПроверка
Слайд 7 «Симметрия является той идеей, с помощью которой человек
веками пытается объяснить и создать порядок, красоту и совершенство»
Герман ВейльСлайд 8 В древности слово «СИММЕТРИЯ» употреблялось в
значении «гармония», «красота».
В переводе с греческого
это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей»
Слайд 9
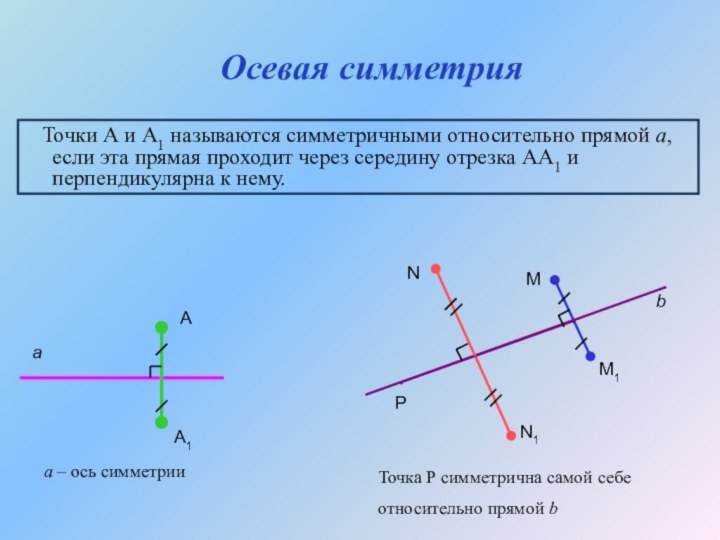
Осевая симметрия
Точки А и А1 называются
симметричными относительно прямой а, если эта прямая проходит через
середину отрезка АА1 и перпендикулярна к нему.а
А
А1
а – ось симметрии
Р
М
М1
b
N
N1
Точка Р симметрична самой себе
относительно прямой b
Слайд 13 У геометрических фигур может быть одна или несколько
осей симметрии, а может и не быть совсем. Мысленно определите,
сколько осей симметрии имеет каждая из фигур?
Слайд 14 У геометрических фигур может быть одна или несколько
осей симметрии, а может и не быть совсем. Мысленно определите,
сколько осей симметрии имеет каждая из фигур?
Слайд 15
Центральная симметрия
Точки А1 и А2 называются симметричными
относительно
точки О, если О – середина отрезка
А1А2А1
А2
О
О
Р
Q
M
M1
N
N1
А1О = ОА2
Точка О – центр симметрии
Слайд 17 Примерами фигур, обладающих центральной симметрией, являются окружность и
параллелограмм
Параллелограмм
Окружность
о
О
Слайд 18
Фигуры, обладающие центральной и осевой симметрией
О
В
А
L
N
D
С
Фигура называется симметричной
относительно точки О, если для каждой точки фигуры симметричная
ей точка относительно точки О также принадлежит этой фигуре.Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
К
М
E
P
b
T
Q
Слайд 20
Определить фигуры:
обладающие центральной симметрией и указать их центр;
обладающие осевой симметрией и указать ось симметрии;имеющие обе симметрии.
Слайд 28
СИММЕТРИЯ В ПРИРОДЕ
Самым ярким примером красоты форм
симметрии являются кристаллы и снежинки. Мало кто знает, что
природные снежинки бывают только шестиугольными или любыми другими образованиями с количеством лучей, кратным трем.
Слайд 29
СИММЕТРИЯ В АРХИТЕКТУРЕ
Примером современных зданий, построенных в
середине ХХ века, является гостиница “Прибалтийская”. Симметричность, как видно
из рисунка присутствует как в общей композиции, так и в каждой из трех его составляющихВ начале XIX века по проекту А.Н. Воронихина было сооружено выдающееся произведение искусства – Казанский собор, имеющий четкие симметричные композиции
Слайд 30
СИММЕТРИЯ В БЫТУ
Издревле люди стремились украсить все,
что окружало их в быту. Они придумывали удивительные замысловатые
орнаменты, в построении которых часто используются принципы симметрии, приёмы ритмичных повторов.
Слайд 31
СИММЕТРИЯ В ИССКУСТВЕ
Симметричная композиция легко воспринимается зрителем,
сразу привлекая внимание к центру картины, в котором и
находится то главное, относительно которого разворачивается действие.
Слайд 32
Природа говорит языком математики: буквы этого языка - круги, треугольники и иные математические фигуры.
Галилей.
