- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Многогранники (Правильные многогранники) 11 класс
Содержание
- 2. ЦЕЛЬ СЕМИНАРА Закрепить и усвоить изученный материал
- 3. С глубокой древности человеку известны пять удивительных многогранников
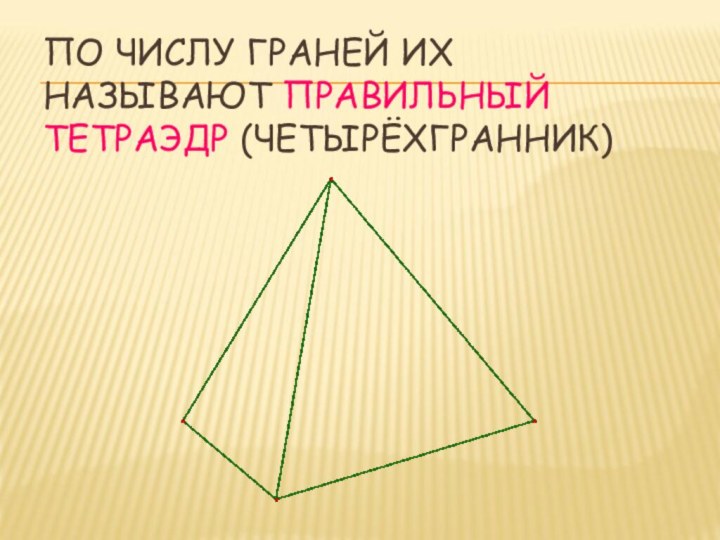
- 4. ПО ЧИСЛУ ГРАНЕЙ ИХ НАЗЫВАЮТ ПРАВИЛЬНЫЙ ТЕТРАЭДР (ЧЕТЫРЁХГРАННИК)
- 5. ГЕКСАЭДР (ШЕСТИГРАННИК) ИЛИ КУБ
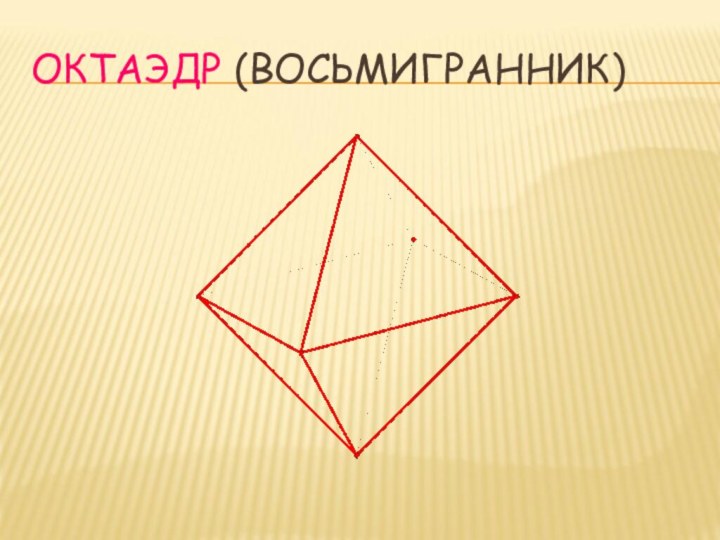
- 6. ОКТАЭДР (ВОСЬМИГРАННИК)
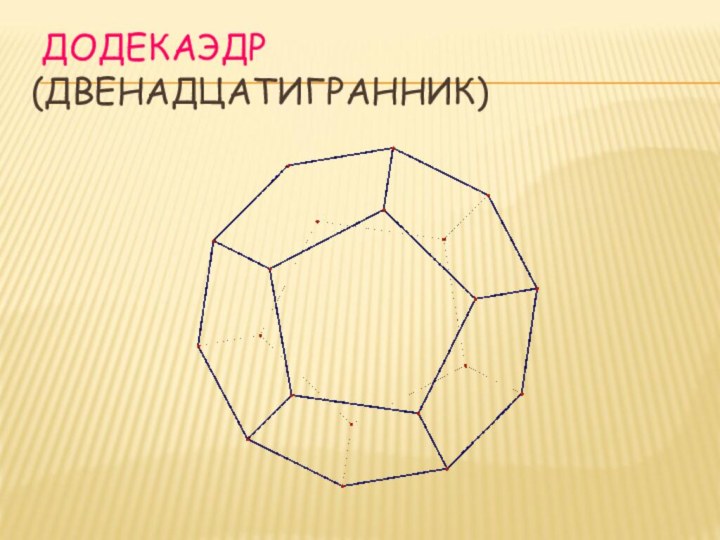
- 7. ДОДЕКАЭДР (ДВЕНАДЦАТИГРАННИК)
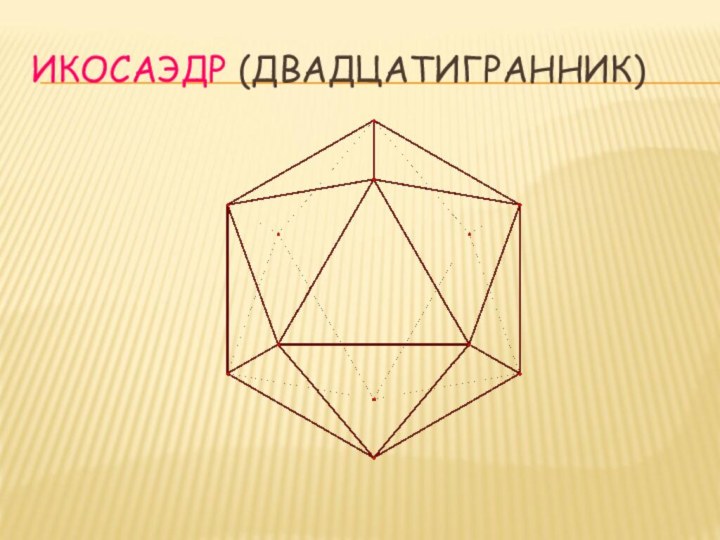
- 8. ИКОСАЭДР (ДВАДЦАТИГРАННИК)
- 9. Свойства этих многогранников изучали ученые и священники,
- 10. Великий древнегреческий философ Платон, живший в IV
- 11. Четыре сущности природы были известны человечеству: огонь,
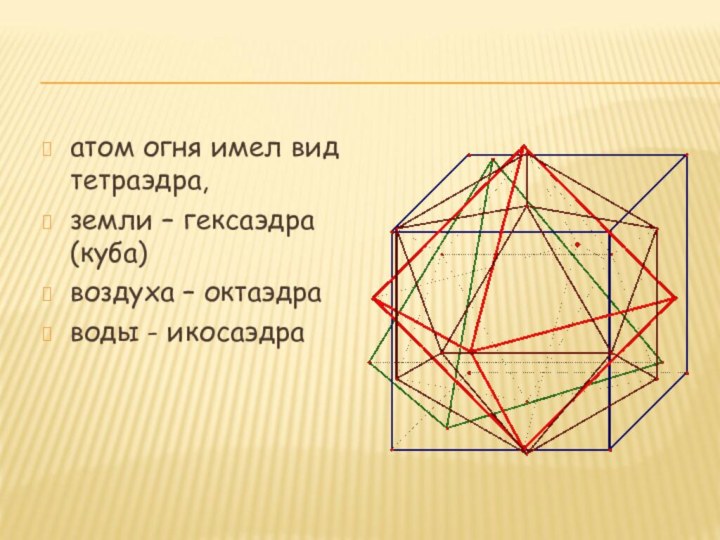
- 12. атом огня имел вид тетраэдра,земли – гексаэдра (куба)воздуха – октаэдраводы - икосаэдра
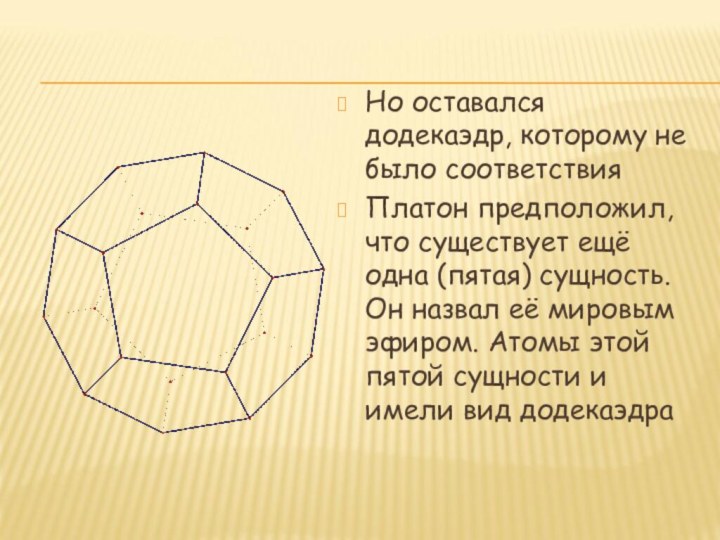
- 13. Но оставался додекаэдр, которому не было соответствия
- 14. Платон и его ученики в своих работах
- 15. ОПРЕДЕЛЕНИЕ ПРАВИЛЬНОГО МНОГОГРАННИКАМногогранник называется правильным, если все
- 16. Платоновы тела - трехмерный аналог плоских правильных
- 17. Доказательство этого факта известно уже более двух
- 18. Существует лишь пять выпуклых правильных многогранников -
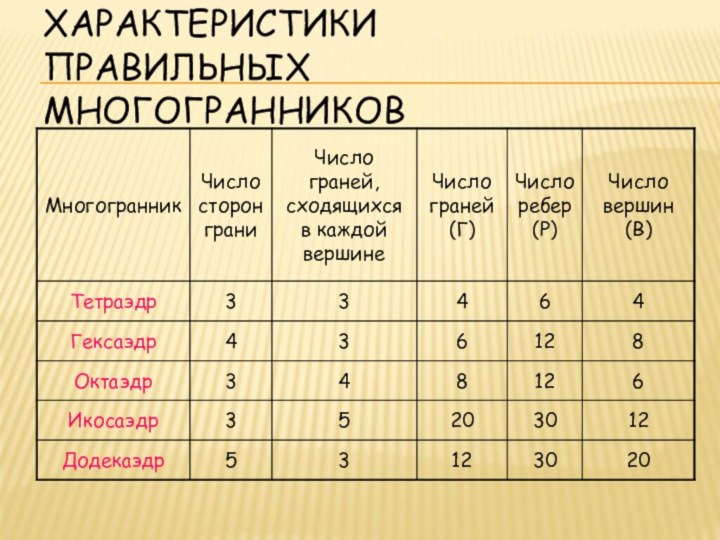
- 19. ХАРАКТЕРИСТИКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
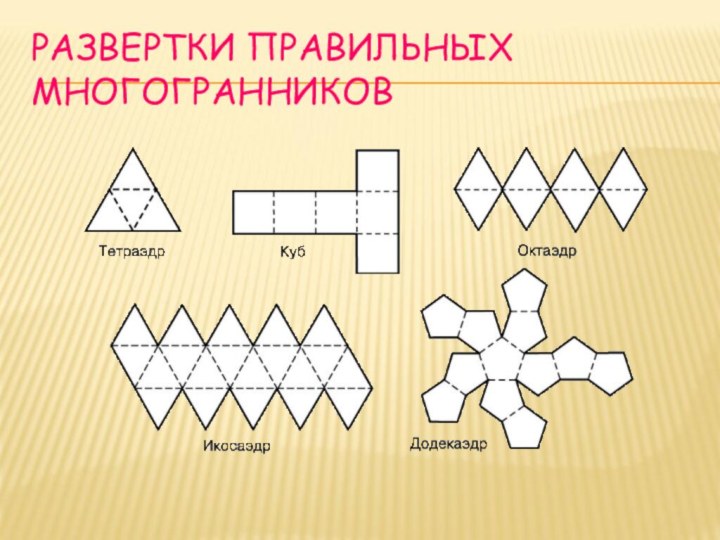
- 20. РАЗВЕРТКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- 21. ДВОЙСТВЕННОСТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВГексаэдр (куб) и октаэдр образуют
- 22. Возьмем любой куб и рассмотрим многогранник с
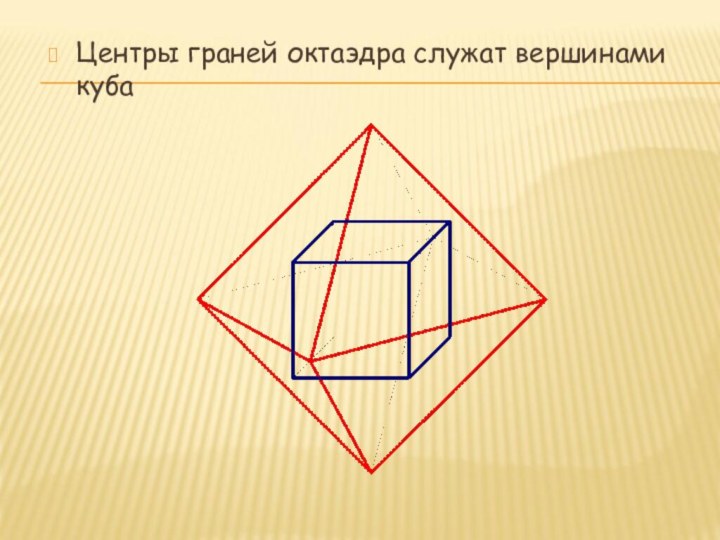
- 23. Центры граней октаэдра служат вершинами куба
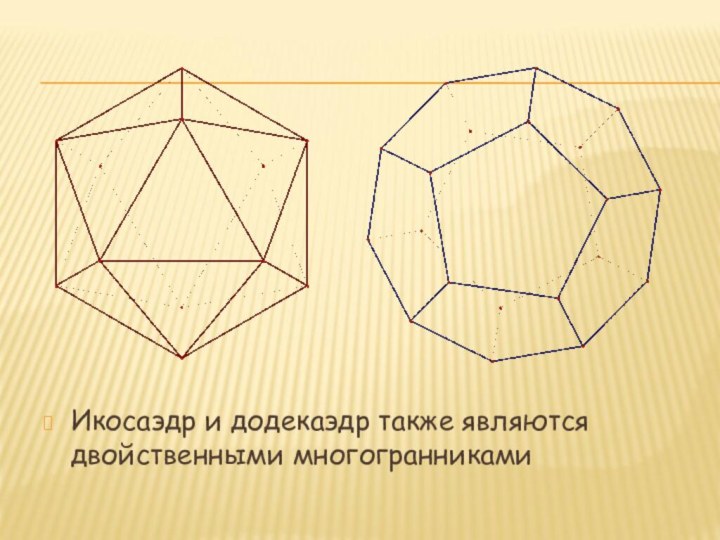
- 24. Икосаэдр и додекаэдр также являются двойственными многогранниками
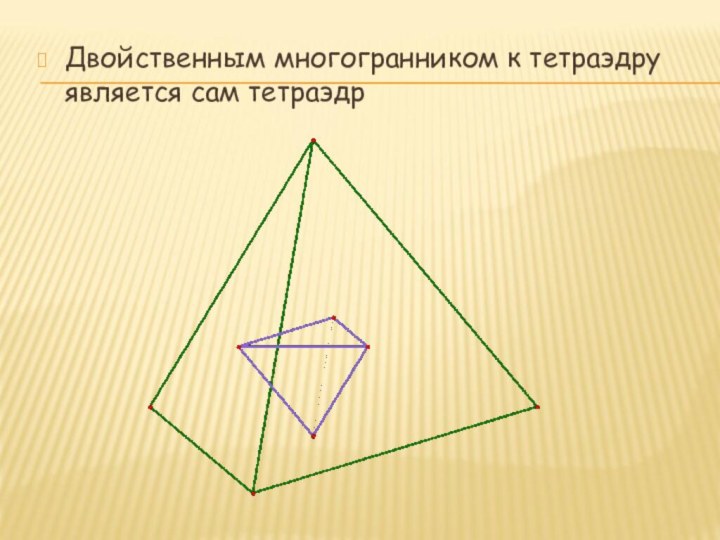
- 25. Двойственным многогранником к тетраэдру является сам тетраэдр
- 26. СОЗДАНИЕ В АРХИТЕКТУРЕ ПРАВИЛЬНЫХ МНОГОГРАННИКОВЧетыре яруса башни представляют из себя куб, многогранники и пирамиду.
- 27. Скачать презентацию
- 28. Похожие презентации
ЦЕЛЬ СЕМИНАРА Закрепить и усвоить изученный материал Узнать новое на данном семинареЭтот материал понадобится нам при сдачи ЗНО. По математике