- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Равнобедренный треугольник (7 класс)
Содержание
- 2. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
- 3. Определение равнобедренного треугольникаСвойство углов равнобедренного треугольникаСвойство биссектрисы равнобедренного треугольника, проведенной к основаниюПЛАН
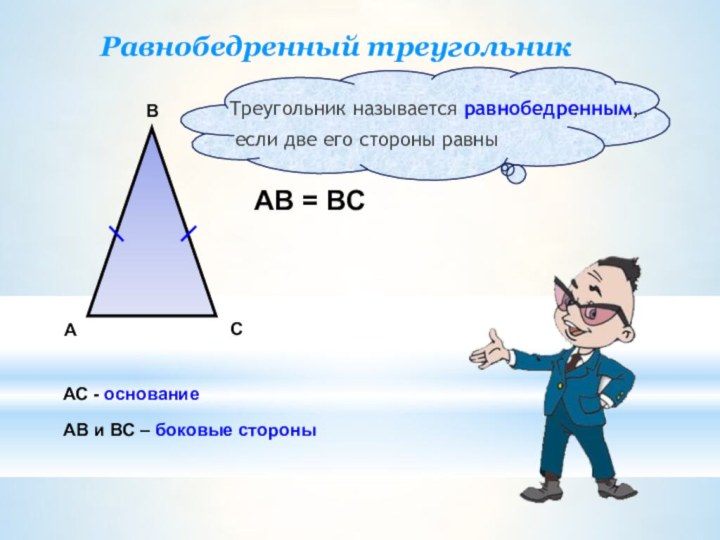
- 4. Треугольник называется равнобедренным, если две его стороны
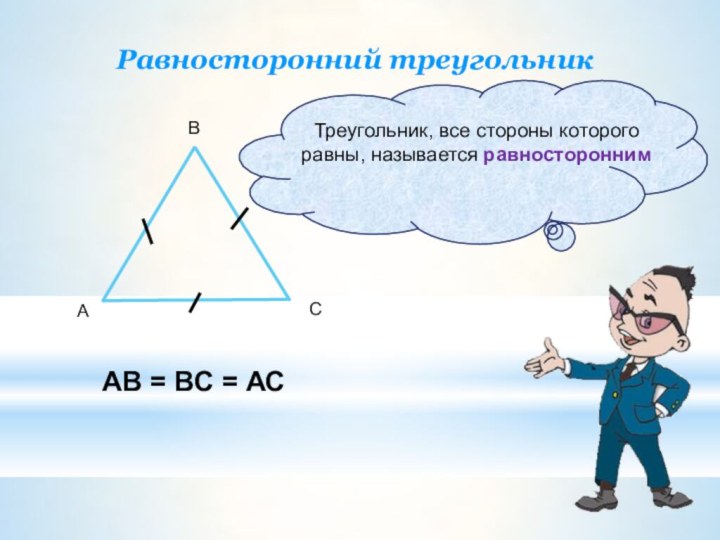
- 5. АВСТреугольник, все стороны которого равны, называется равностороннимАВ = ВС = АСРавносторонний треугольник
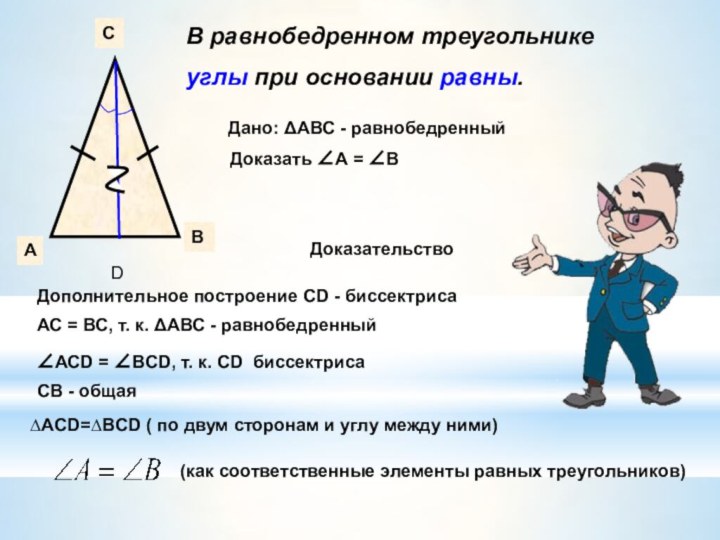
- 6. АВСВ равнобедренном треугольнике углы при основании равны.Дополнительное
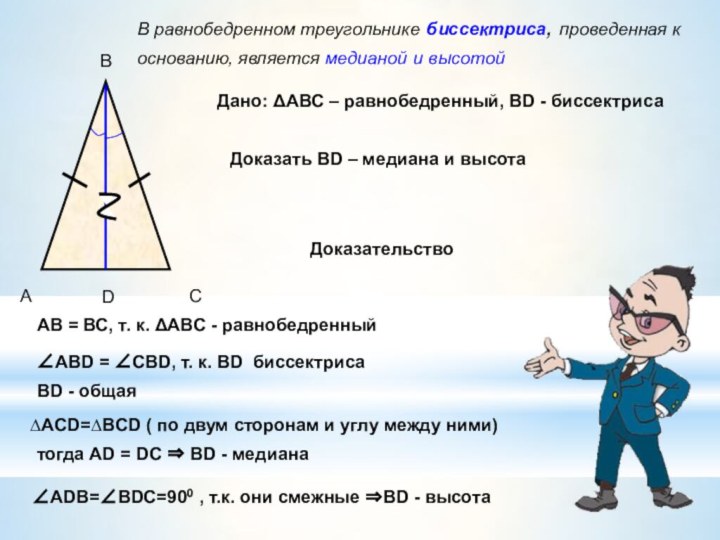
- 7. АВСВ равнобедренном треугольнике биссектриса, проведенная к основанию,
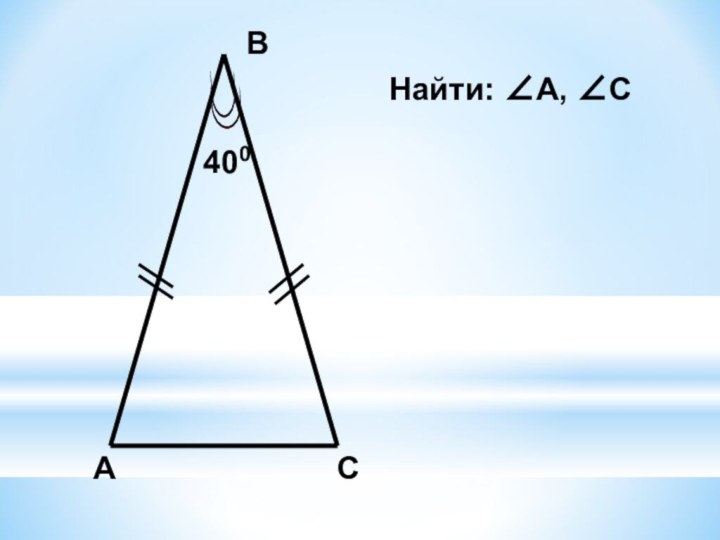
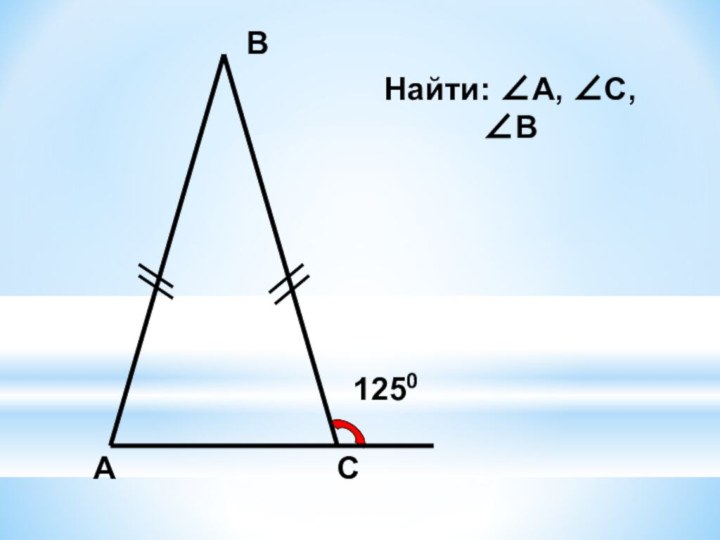
- 8. АВС400Найти: ∠А, ∠С
- 9. Скачать презентацию
- 10. Похожие презентации
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК



Слайд 3
Определение равнобедренного треугольника
Свойство углов равнобедренного треугольника
Свойство биссектрисы равнобедренного
треугольника, проведенной к основанию
Слайд 4
Треугольник называется равнобедренным,
если две его стороны равны
A
B
C
АВ
= ВС
АВ и ВС – боковые стороны
АС - основание
Равнобедренный
треугольник
Слайд 5
А
В
С
Треугольник, все стороны которого равны, называется равносторонним
АВ =
ВС = АС
Равносторонний треугольник
Слайд 6
А
В
С
В равнобедренном треугольнике
углы при основании равны.
Дополнительное построение
CD - биссектриса
∆ACD=∆BCD ( по двум сторонам и углу
между ними)Дано: ΔАВС - равнобедренный
Доказать ∠А = ∠В
Доказательство
АС = ВС, т. к. ΔАВС - равнобедренный
∠АСD = ∠ВCD, т. к. CD биссектриса
СВ - общая
(как соответственные элементы равных треугольников)
Слайд 7
А
В
С
В равнобедренном треугольнике биссектриса, проведенная к основанию, является
медианой и высотой
тогда AD = DC ⇒ BD -
медиана∠ADВ=∠ВDC=900 , т.к. они смежные ⇒BD - высота
Дано: ΔАВС – равнобедренный, BD - биссектриса
Доказать BD – медиана и высота
Доказательство
АВ = ВС, т. к. ΔАВС - равнобедренный
∠АВD = ∠СВD, т. к. ВD биссектриса
ВD - общая
∆ACD=∆BCD ( по двум сторонам и углу между ними)