- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельность в пространстве
Содержание
- 2. Параллельные прямые в пространстве;Признак параллельности прямых;Параллельность прямой и плоскости;Параллельность плоскостей;Свойства параллельных плоскостей;Изображение пространственных фигур на плоскости;Содержание:
- 3. Две прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ,если они
- 4. ТЕОРЕМА: Две прямые,параллельные третьей прямой,параллельны.ДОК-ВО:Пусть b и
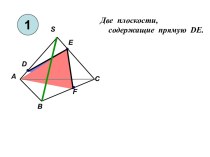
- 5. ТЕОРЕМА: Две плоскости параллельны, если одна из
- 6. ТЕОРЕМА:Если две параллельные плоскости пересекаются третьей,то прямые
- 7. ТЕОРЕМА:Через точку плоскости можно провести плоскость ,параллельную
- 8. Отрезки параллельных прямых,заключённые между двумя параллельными плоскостями,равны.Теорема:аВ1bА1А2В2 а2 а1
- 9. 1 СВОЙСТВО:Прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками.Изображение пространственных фигур на плоскости.АА1 ВВ1СС1h
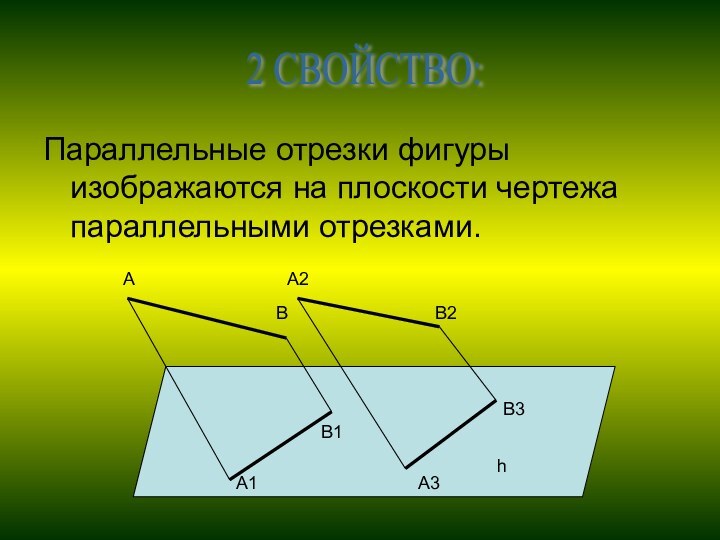
- 10. Параллельные отрезки фигуры изображаются на плоскости чертежа параллельными отрезками.2 СВОЙСТВО:АА1В1В3В2А2А3Вh
- 11. Отношение отрезков одной прямой или параллельных прямых сохраняется при параллельном проектировании.3 СВОЙСТВО:АВА1А2В1hКК2К1
- 12. Скачать презентацию
- 13. Похожие презентации
Параллельные прямые в пространстве;Признак параллельности прямых;Параллельность прямой и плоскости;Параллельность плоскостей;Свойства параллельных плоскостей;Изображение пространственных фигур на плоскости;Содержание:











Слайд 2
Параллельные прямые в пространстве;
Признак параллельности прямых;
Параллельность прямой и
плоскости;
Слайд 3 Две прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ,если они лежат
в одной плоскости и не пересекаются.
ТЕОРЕМА:Через точку вне данной
прямой можно провести прямую,параллельную этой прямой ,и притом только одну.Док-во:Пусть а- данная прямая и А-точка ,не лежащая на этой прямой.Проведем через прямую а и точку А плоскость а.Проведем через точку А в плоскости h прямую а1,параллельная а,единственна.Допустим,что а2,проходящая через А и параллельна а.Через а и а2 можно провести плоскость h2.Плоскость h2 проходит через а и А;следовательно,по т.1.1 она совпадает с h. По аксиоме параллельных прямые а1 и а2 совпвдают.
Параллельные прямые в пространстве.
А
h
а
а
1
Слайд 4
ТЕОРЕМА: Две прямые,параллельные третьей прямой,параллельны.
ДОК-ВО:Пусть b и c
параллельны а.Докажем,что b и с параллельны.Пусть k-плоскость,в которой лежат
a и b ,h-плоскость,в которой лежат а и с.Плоскости k и h различны.Отметим на k точку В и проведём плоскость h1 через с и В.Она пересечёт k по прямой b1.Прямая b1 не пересекает h.Точка пересечения должна принадлежать прямой а,т.к. прямая b1 лежит в плоскости k.
Т.к. прямая b1 лежит в плоскости k и не пересекает прямую а,то она параллельна а,а значит,совпадает с b по аксиоме параллельных.Прямая b,совпадая с прямой b1,лежит в одной плоскости с прямой с и не пересекает её.Значит b и с параллельны.
Признак параллельности прямых.
b
h
h1
b1
k
с
а
В
Слайд 5 ТЕОРЕМА: Две плоскости параллельны, если одна из них
параллельна двум пересекающимся прямым, лежащим в другой плоскости
ДОК-ВО: Пусть
k и h – данные плоскости и b1.b2 – две пересекающиеся прямые в плоскости h, параллельные плоскости k. Плоскости k и h, различны. Допустим , что они пересекаются по некоторой прямой с. Прямые b1 и b2 не пересекают плоскость k; следовательно не пересекают прямую с этой плоскости. Но это возможно по аксиоме параллельных, т.к. лежащие в плоскости h пересекающиеся прямые b1 и b2 параллельны одной и той же прямой с. Мы пришли к противоречию. Параллельность плоскостей
k
b1
b2
с
h
Слайд 6 ТЕОРЕМА:Если две параллельные плоскости пересекаются третьей,то прямые пересечения
параллельны.
ДОК-ВО:Согласно определению параллельные прямые- это прямые ,которые лежат в
одной плоскости – секущей плоскости.Они не пересекаются ,так как не пересекаются содержащие их параллельные плоскости. Значит,прямые параллельны.Теорема доказана.Параллельность плоскостей.
Слайд 7 ТЕОРЕМА:Через точку плоскости можно провести плоскость ,параллельную данной
, и притом только одну.
Параллельность плоскостей.
b1
а1
а
b
h
k.
b2
a 2