- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Медианы треугольника. 7 класс.
Содержание
- 2. Содержание:Место данной темы в программе обучения. Цели
- 3. Виды треугольниковОстроугольныеПрямоугольныеТупоугольные
- 4. Повторим
- 5. Повторим
- 6. Найди медиану
- 7. Найди медиану
- 8. Найди медиану
- 9. Виды треугольниковРавнобедренныеРавносторонние
- 10. Повторим
- 11. Повторим
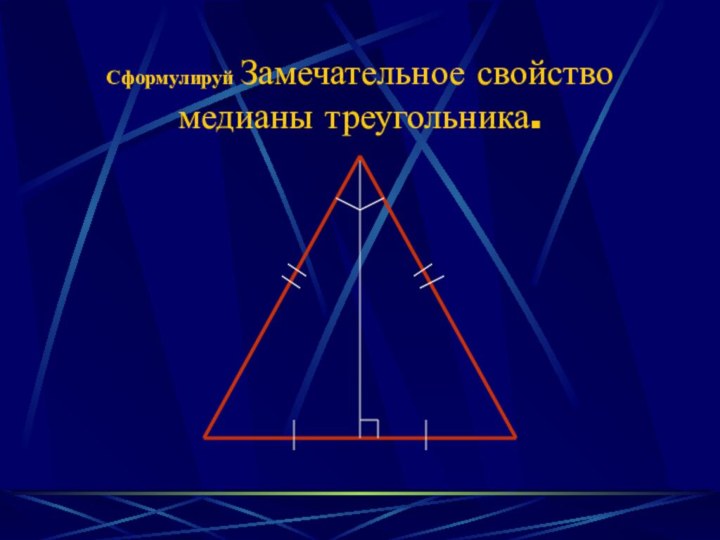
- 12. Сформулируй Замечательное свойство медианы треугольника.
- 13. Замечательное свойство медианы треугольника. - медиана, проведенная
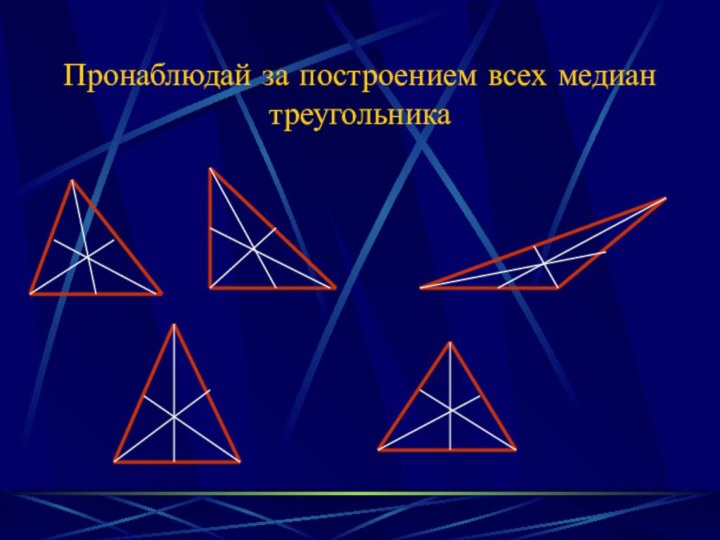
- 14. Пронаблюдай за построением всех медиан треугольника
- 15. Сверь свой вывод со следующим Замечательным свойством
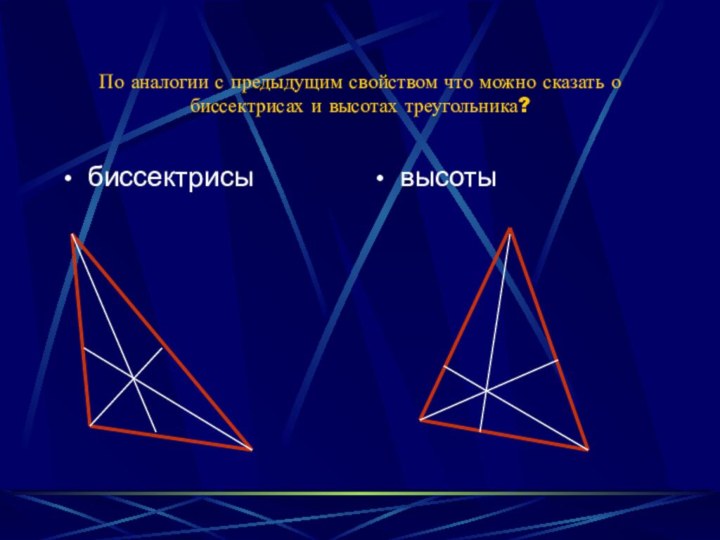
- 16. По аналогии с предыдущим свойством что можно сказать о биссектрисах и высотах треугольника?биссектрисывысоты
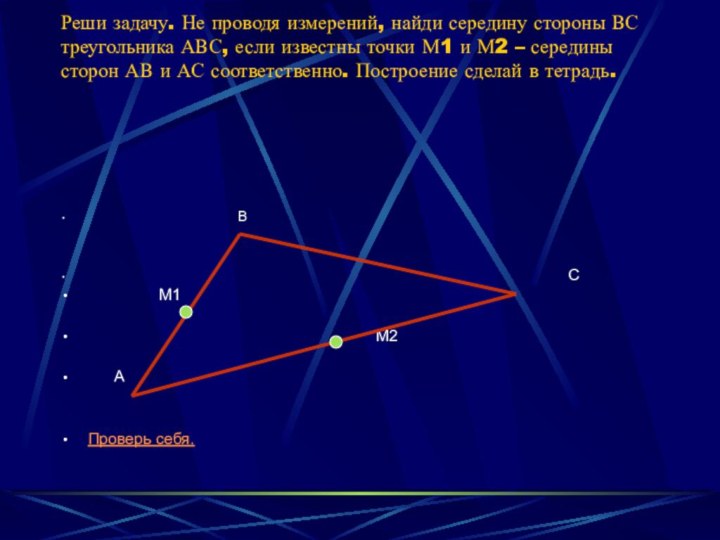
- 17. Реши задачу. Не проводя измерений, найди середину
- 18. Проверь себя!Проведу медиану ВМ1.Проведу медиану СМ2.Через точки
- 19. Найди необходимые тебе определения и повтори их.
- 20. верно
- 21. Скачать презентацию
- 22. Похожие презентации
Содержание:Место данной темы в программе обучения. Цели и задачи.Обобщение изученного по теме «Медианы треугольника».Решение задач. Теоретический материал.Тест «Верно-неверно».

















Слайд 13
Замечательное свойство медианы треугольника.
- медиана, проведенная к
основанию равнобедренного треугольника, является
-диаметром и высотой;
-биссектрисой и основанием;
-высотой и
основанием;-высотой и биссектрисой;
-биссектрисой и диаметром.
Забыл?
А что происходит в равностороннем треугольнике?
Слайд 15 Сверь свой вывод со следующим Замечательным свойством медиан
треугольника
Медианы в любом виде треугольника
пересекаются в одной
точке.
Слайд 16 По аналогии с предыдущим свойством что можно сказать
о биссектрисах и высотах треугольника?
биссектрисы
высоты
Слайд 17 Реши задачу. Не проводя измерений, найди середину стороны
ВС треугольника АВС, если известны точки М1 и М2
– середины сторон АВ и АС соответственно. Построение сделай в тетрадь.
В
С
М1
М2
А
Проверь себя.
Слайд 18
Проверь себя!
Проведу медиану ВМ1.
Проведу медиану СМ2.
Через точки А
и точку пересечения медиан проведу отрезок до пересечения со
стороной ВС.Полученный отрезок является медианой треугольника АВС, т.к. медианы любого треугольника пересекаются в одной точке.
тест
Слайд 19 Найди необходимые тебе определения и повтори их. 1. Если
из вершины треугольника провести прямую (или ее продолжение) под
прямым углом, то отрезок этой прямой от вершины до стороны (или ее продолжения) называется высотой треугольника. 2. Если середину стороны треугольника соединить с противоположной вершиной, то полученный отрезок называется медианой треугольника. 3. Если провести биссектрису угла треугольника, то ее отрезок от вершины до противоположной стороны называют биссектрисой треугольника. 4. В каждом треугольнике можно провести три биссектрисы, три медианы, три высоты. 5. В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты (и продолжения высот – в тупоугольном треугольнике) пересекаются в одной точке. Все три точки совпадают только в равностороннем треугольнике. 6. Равнобедренный треугольник – это треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. 7. Замечательное свойство равнобедренного треугольника: - биссектриса, проведенная к основанию треугольника, является его медианой и высотой; - медиана, проведенная к основанию треугольника, является его биссектрисой и высотой; - высота, проведенная к основанию треугольника, является его медианой и биссектрисой. 8. Треугольник, у которого все стороны равны, называется равносторонним. 9. Виды треугольников: остроугольный прямоугольный тупоугольный равнобедренный равносторонний





























