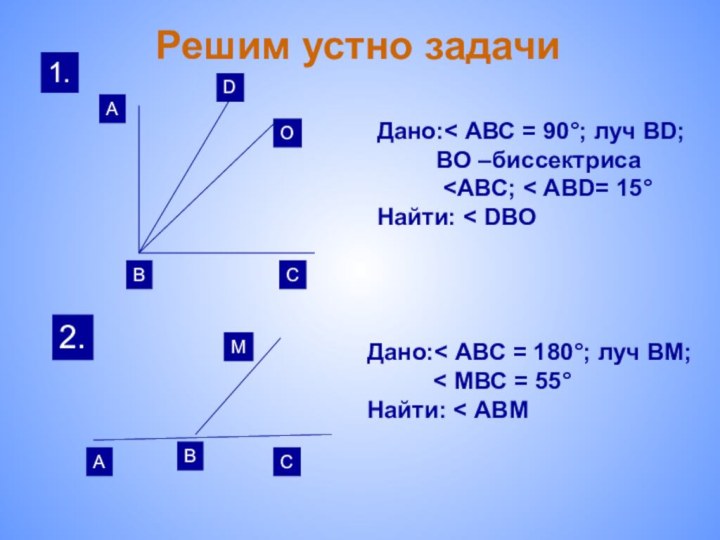
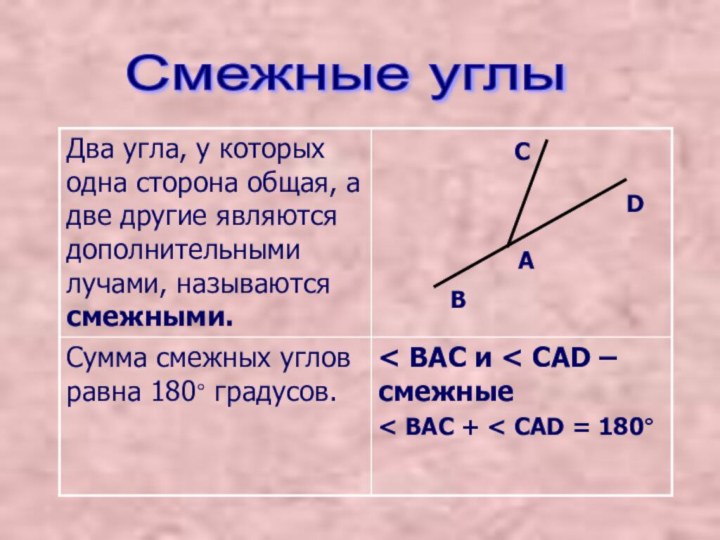
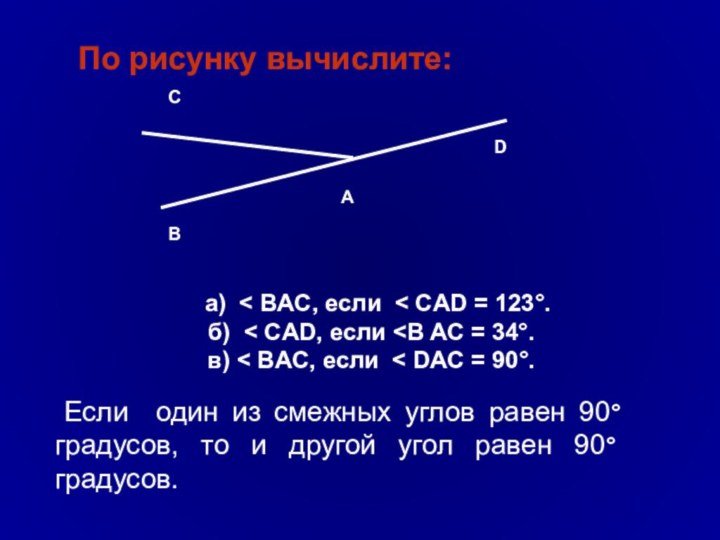
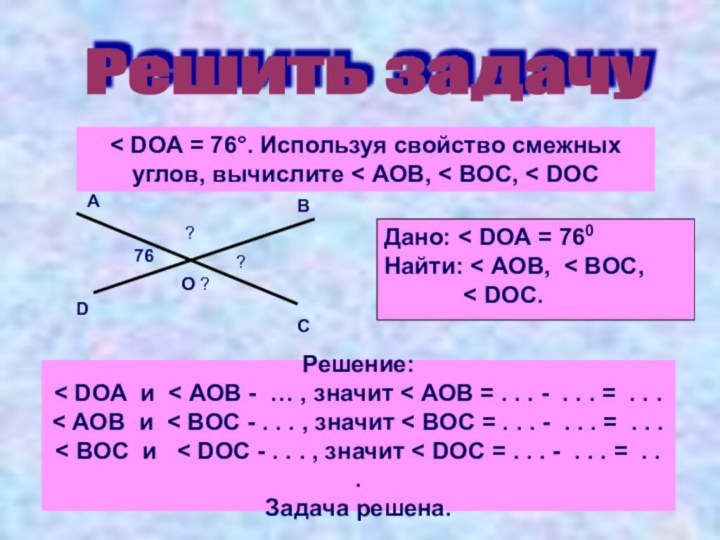
называются смежными и
вертикальными; познакомимся с их свойствами;
Какие прямые
называются перпендикулярными;Будем учиться решать задачи, используя эти
свойства.
Эпиграф к нашему уроку:
Ум хорошо,
а два лучше !