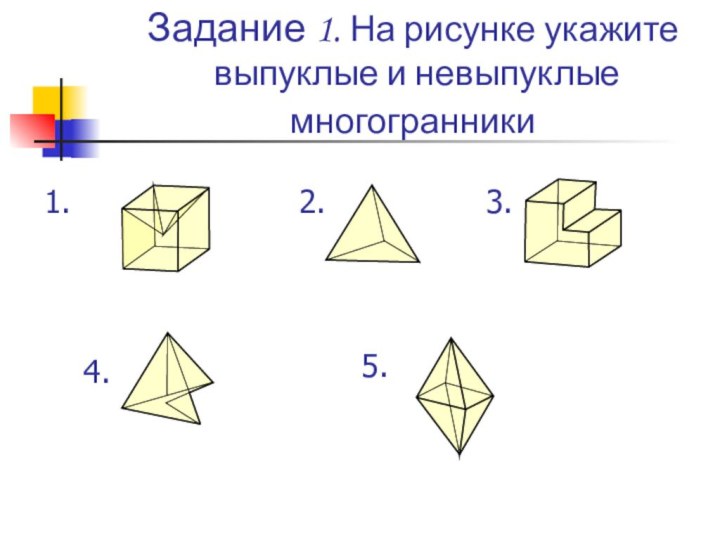
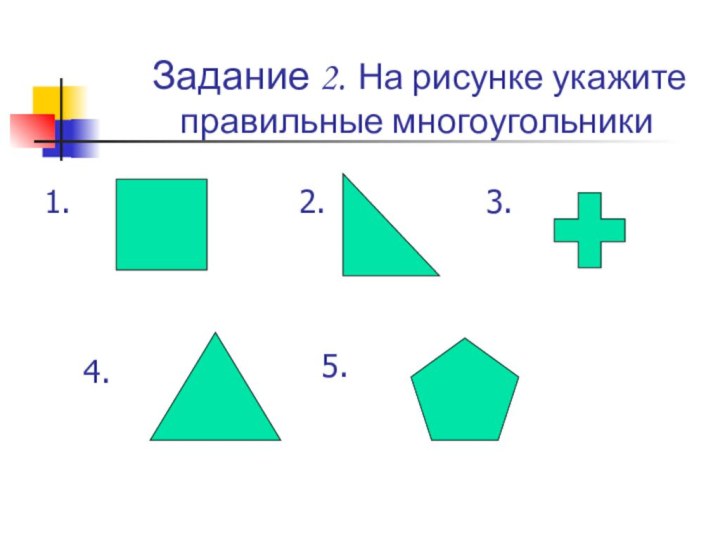
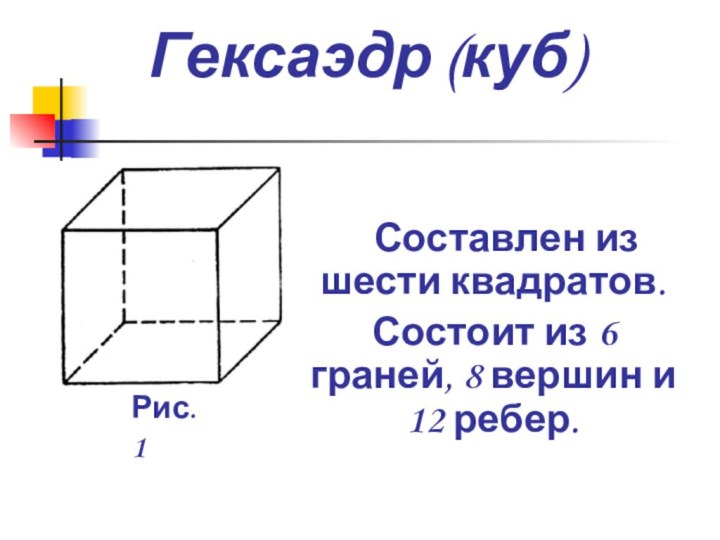
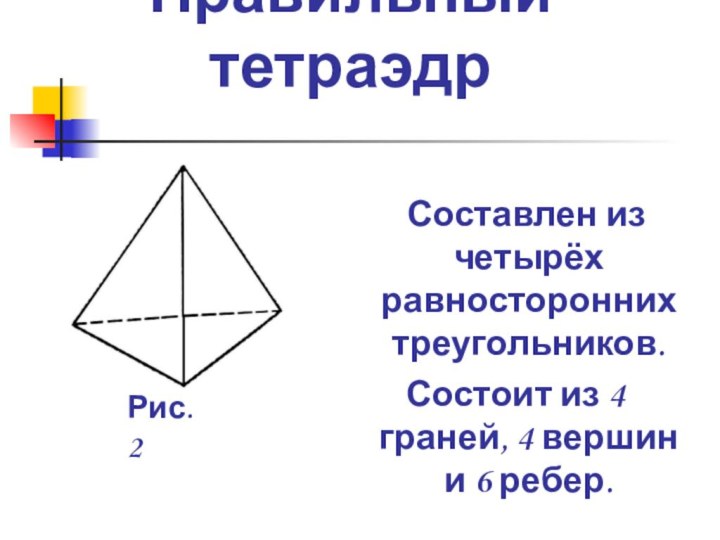
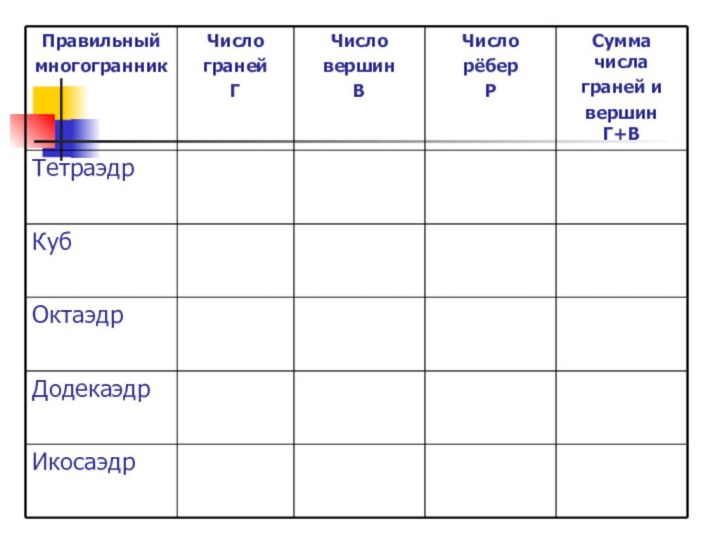
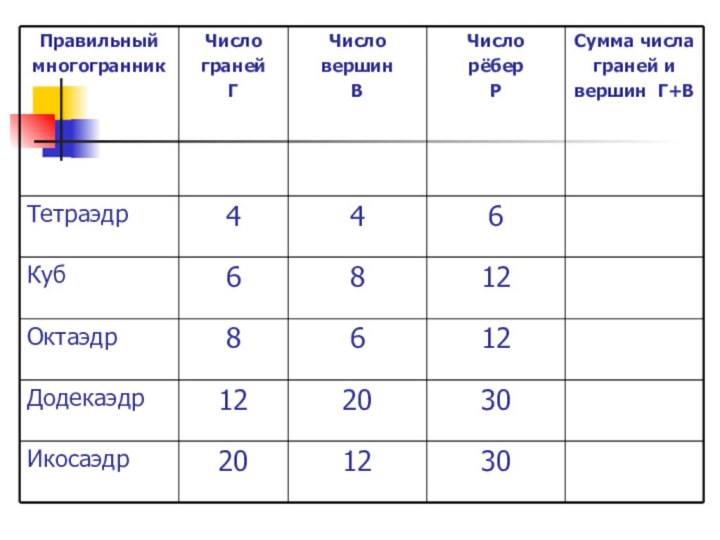
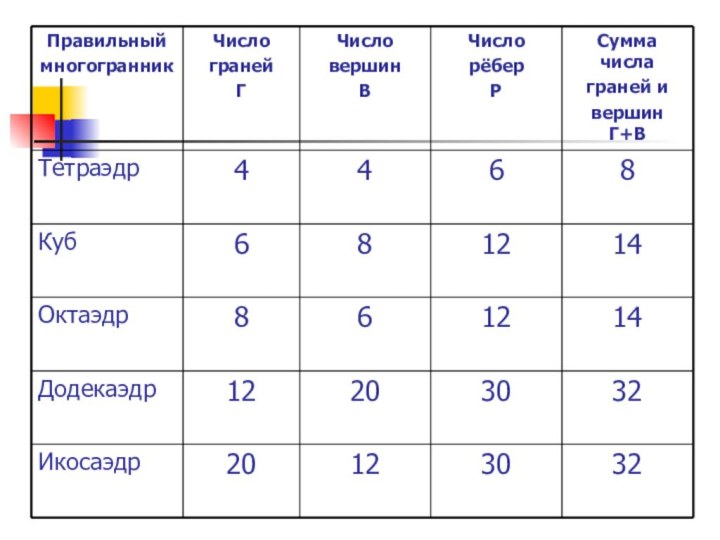
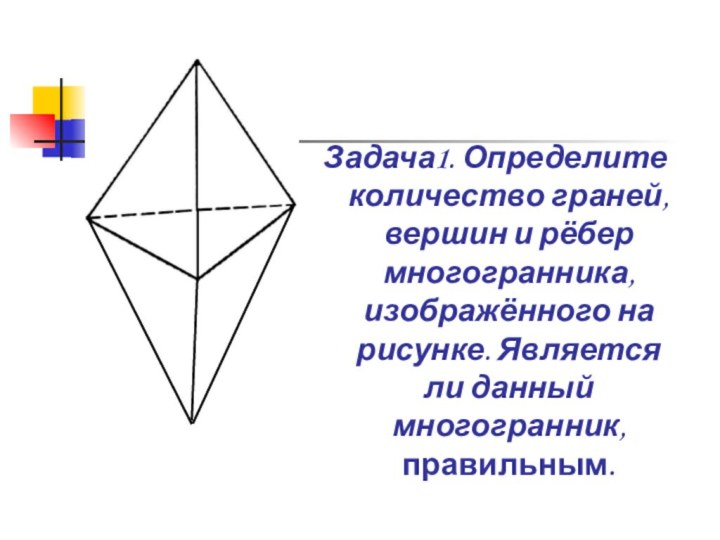
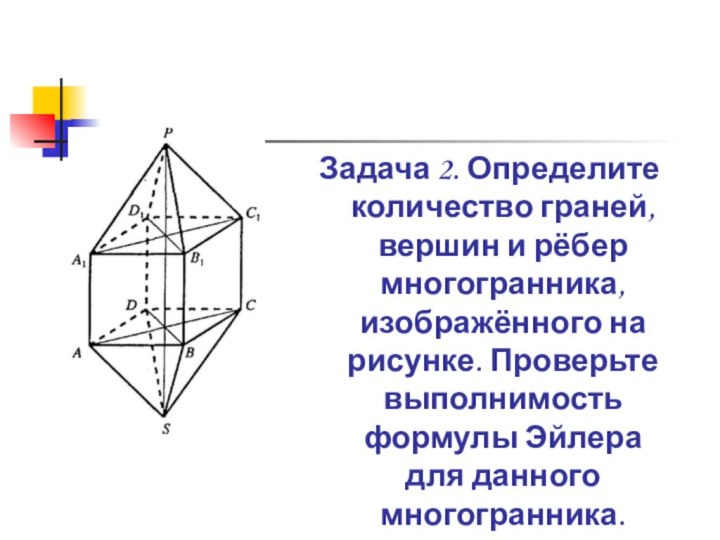
сформулировать теорему Эйлера.
3. Показать влияние правильных многогранников на возникновение
философских теорий и фантастических гипотез. 4. Показать связь геометрии и природы.