Слайд 3
Продолжите предложение:
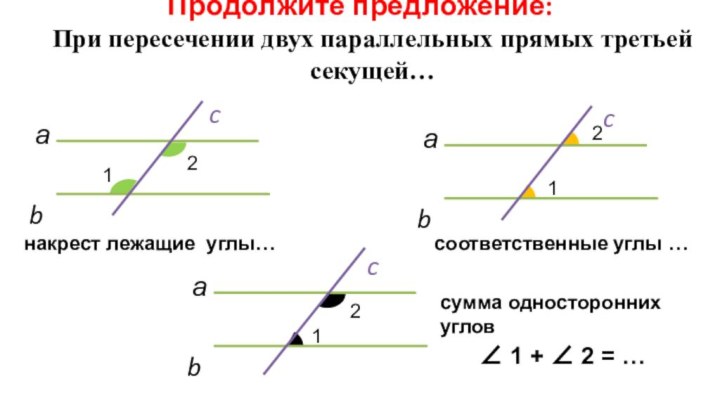
При пересечении двух параллельных прямых третьей секущей…
а
c
b
а
c
b
а
c
b
∠ 1 + ∠ 2 = …
1
2
1
1
2
2
накрест лежащие углы…
соответственные
углы …
сумма односторонних углов
Слайд 4
Продолжите предложение:
При пересечении двух параллельных прямых третьей секущей…
а
c
b
а
c
b
а
c
b
∠ 1 + ∠ 2 = 180°
1
2
1
1
2
2
накрест лежащие углы
равны
соответственные углы равны
сумма односторонних углов
Слайд 5
Продолжите предложение:
Два треугольника равны, если …
Слайд 6
:
Продолжите предложение: Два треугольника равны, если …
одного ∆ соответственно равны …
две стороны и угол между
ними
сторона и два прилежащих к ней угла
три стороны
Слайд 7
А
B
C
D
AB ⎢⎢CD, AC ⎢⎢BD
Определение
Четырехугольник, у которого противоположные
стороны попарно параллельны, называется параллелограммом
Слайд 8
На каком из чертежей изображён параллелограмм?
АВ=СD
BC=DA
А
B
D
C
АO=OC
BO=OD
А
B
D
C
O
А
B
D
C
АВСD
квадрат
А
B
D
C
АВ=АD
СD=СВ
А
B
D
C
Нет
АВ║DС
А
B
D
C
Слайд 9
Свойства параллелограмма
1
В параллелограмме противоположные
стороны равны и
противоположные
углы равны.
∠1 = ∠2, ∠3 = ∠4
ВС
= AD, АВ = СD
Слайд 10
Свойства параллелограмма
2
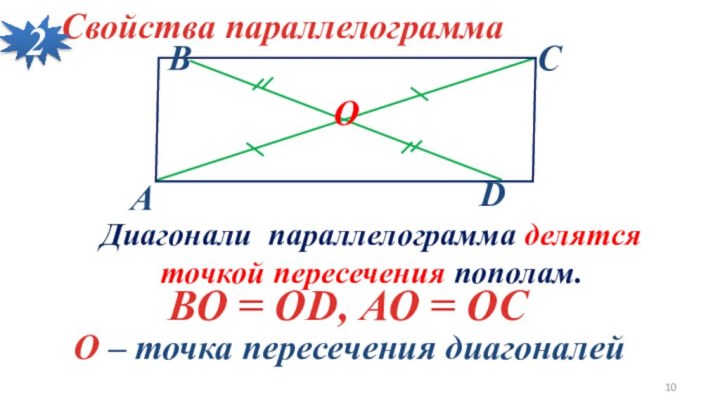
Диагонали параллелограмма делятся точкой пересечения пополам.
О
ВО =
ОD, АО = ОС
О – точка пересечения диагоналей
Слайд 11
Признаки параллелограмма
2
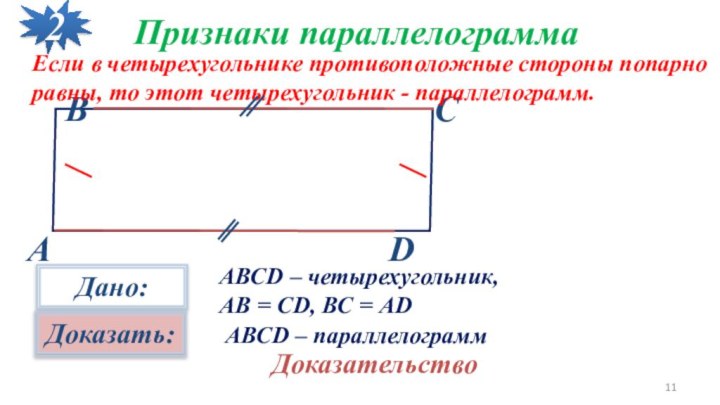
Если в четырехугольнике противоположные стороны попарно
равны,
то этот четырехугольник - параллелограмм.
АВСD – четырехугольник,
АВ =
CD, ВС = АD
АВСD – параллелограмм
Доказательство
Слайд 12
2
АВСD- четырехугольник,
АВ = CD, ВС = АD.
Доказательство
Рассмотрим треугольники
∆ АBC и ∆ACD:
∆ АBC =
∆ACD – по трем сторонам
(АС – общая, АВ = СD, ВС = АD – по условию).
Поэтому ∠1 = ∠ 2 как накрест лежащие при секущей АС.
Отсюда следует, что АВ ∥ СD.
Проведем диагональ АС.
Так как АВ ∥ СD и АВ = СD, то по признаку 1 четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
Слайд 13
Свойства параллелограмма
3
В параллелограмме сумма углов, прилежащих к одной
стороне, равна 180°.
∠А + ∠D = 180° ,
∠D +
∠C = 180° ,
∠А + ∠B = 180° ,
∠В + ∠C = 180° ,
Слайд 14
30.11.2012
www.konspekturoka.ru
3
О
Признаки параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой
пересечения делятся пополам, то этот четырехугольник параллелограмм.
АВСD – четырехугольник,
ВО = ОD, АО = ОС
АВСD – параллелограмм
Доказательство
Слайд 15
30.11.2012
www.konspekturoka.ru
3
О
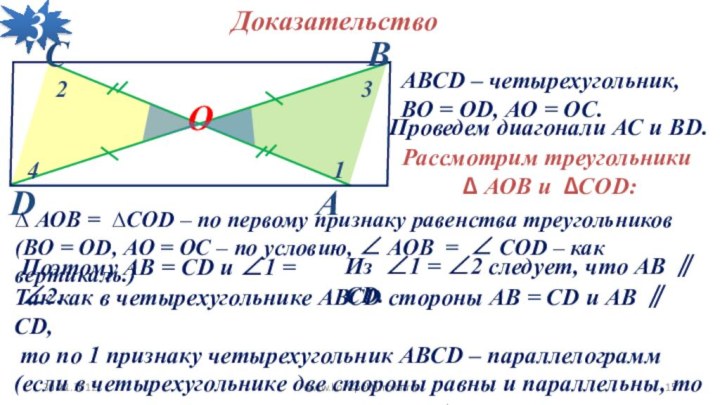
АВСD – четырехугольник,
ВО = ОD, АО =
ОС.
Доказательство
Проведем диагонали АС и BD.
Рассмотрим треугольники
∆ АОB
и ∆CОD:
∆ АОB = ∆CОD – по первому признаку равенства треугольников
(ВО = ОD, АО = ОС – по условию, ∠ АОB = ∠ CОD – как вертикаль.)
Поэтому АВ = CD и ∠1 = ∠2.
Из ∠1 = ∠2 следует, что АВ ∥ CD.
Так как в четырехугольнике АВСD стороны АВ = CD и АВ ∥ CD,
то по 1 признаку четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
Слайд 16
1
АВСD – четырехугольник,
∠BАC = ∠ACD, ∠CAD =∠BCA
АВСD
– параллелограмм.
Доказательство
Рассмотрим треугольники ∆ АBC
и ∆ACD:
1. ∠BАC
= ∠ACD, ∠CAD =∠BCA – по
условию, АС – общая;
следовательно ∆ АBC = ∆ACD – по
стороне и двум прилежащим углам;
поэтому ВС = AD.
2.Так как ∠BАC = ∠ACD – накрест лежащие углы при
параллельных прямых ВС, AD и секущей - АС, то ВС ∥ AD.
3.Так как ВС = AD и ВС ∥ AD, то по 1-му признаку параллелограмма АВСD – параллелограмм, что и требовалось доказать.
Задача
Слайд 17
Свойство 2. Диагонали параллелограмма точкой пересечения
делятся пополам.
В
А
С
D
1
3
4
Дано: АВСD - параллелограмм
Доказать: ВО = ОD, АО
= ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
O
АВ = СD (противоположные стороны параллелограмма,
2
Слайд 18
Решите задачу. В параллелограмме ABCD: О
– точка пересечения диагоналей, отрезок MK проходит через эту
точку.
A
Решение: по свойству параллелограмма ВО = ОD, ∠ ВОМ =∠ КОD – вертикальные ,
∠ МВО = ∠ DОК – накрест лежащие при параллельных прямых ВМ и DК и секущей ВD ⇒ ∆OMB = ∆OKD (по стороне и двум прилежащим углам).
Докажите, что ∆OMB = ∆OKD
B
C
D
O
Слайд 19
Признаки параллелограмма
1
Если в четырехугольнике две стороны равны и
параллельны,
то этот четырехугольник параллелограмм.
АВСD – четырехугольник,
АВ
= CD, АВ ∥ CD
АВСD – параллелограмм
Доказательство
Слайд 20
1
Доказательство
Пусть АВ = СD и АВ ∥ СD,
проведем диагональ АС.
Рассмотрим треугольники
∆ АBC и ∆ACD:
∆
АBC = ∆ACD – по двум сторонам и углу между ними
(АС – общая, АВ = СD – по условию, ∠1 = ∠ 2 как накрест лежащие при АВ ∥ СD и секущей АС.
Поэтому ∠3 = ∠ 4.
1
2
3
4
Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых
ВС и AD секущей – АС. Следовательно ВС∥ AD.
Таким образом, если в четырехугольнике противоположные
стороны параллельны, то этот четырехугольник АВСD -
параллелограмм.
Слайд 21
Середины сторон произвольного четырёхугольника являются вершинами параллелограмма
Что
за точки отмечаются на четырёхугольниках, какие фигуры получаются при
их соединении?
Теорема Вариньона
Слайд 23
Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно
параллельны.
Слайд 24
Свойства параллелограмма
Свойство 1. Сумма углов параллелограмма, прилежащих к
одной стороне равна 180о.
Доказательство. Углы, прилежащие к стороне параллелограмма,
являются внутренними односторонними углами. Поэтому их сумма равна 180о.
Слайд 25
Свойство 2. В параллелограмме противоположные стороны равны и
противоположные углы равны.
Доказательство. Пусть АВСD – параллелограмм. Диагональ АС
разбивает его на два треугольника АВС и CDA, которые равны по второму признаку равенства треугольников (АС - общая сторона, ∠1 =∠2 и ∠3 = ∠4, как внутренние накрест лежащие углы). Поэтому АВ=CD, BC=AD и ∠B =∠ D. Кроме этого, ∠ A =∠1 +∠3 = ∠2 + ∠4 =∠C.
Слайд 26
Доказательство. Пусть ABCD – параллелограмм, О – точка
пересечения его диагоналей. ∆ AOD=∆COB по второму признаку равенства
треугольников (АD=BC по свойству 2, ∠1 = ∠2 и ∠ 3 = ∠ 4, как внутренние накрест лежащие углы). Поэтому АО = ОС и BO = OD.
Слайд 27
Вопрос 1
Какой четырехугольник называется параллелограммом?
Ответ: Параллелограммом называется
четырехугольник, у которого противоположные стороны попарно параллельны.
Слайд 28
Вопрос 2
Чему равна сумма углов параллелограмма, прилежащих к
одной стороне.
Ответ: 180о.
Слайд 29
Вопрос 3
Что можно сказать о противоположных: а) сторонах;
б) углах параллелограмма?
Ответ: В параллелограмме противоположные стороны равны и
противоположные углы равны.
Слайд 30
Вопрос 4
Что можно сказать о диагоналях параллелограмма?
Ответ: Диагонали
параллелограмма точкой пересечения делятся пополам.
Слайд 31
Упражнение 1
Изобразите параллелограмм ABCD, три вершины которого даны
на рисунке.
Слайд 32
Упражнение 2
Изобразите параллелограмм ABCD, три вершины которого даны
на рисунке.
Слайд 33
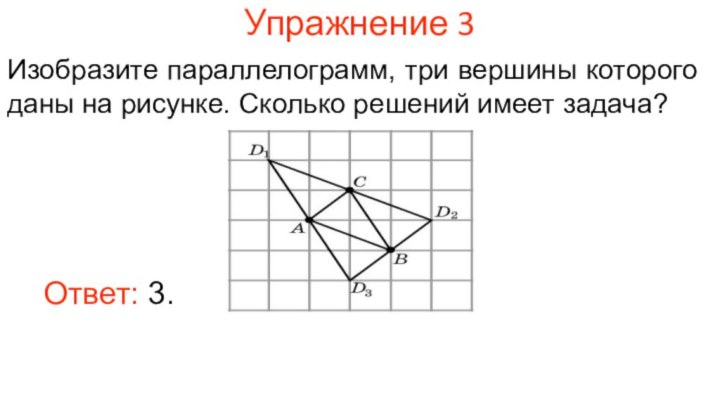
Упражнение 3
Изобразите параллелограмм, три вершины которого даны на
рисунке. Сколько решений имеет задача?
Слайд 34
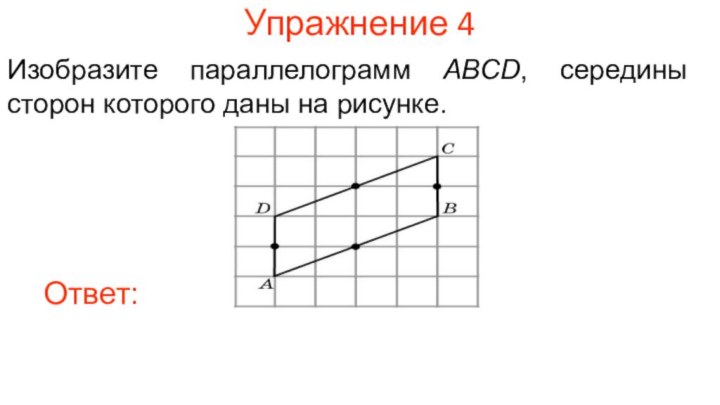
Упражнение 4
Изобразите параллелограмм ABCD, середины сторон которого даны
на рисунке.
Слайд 35
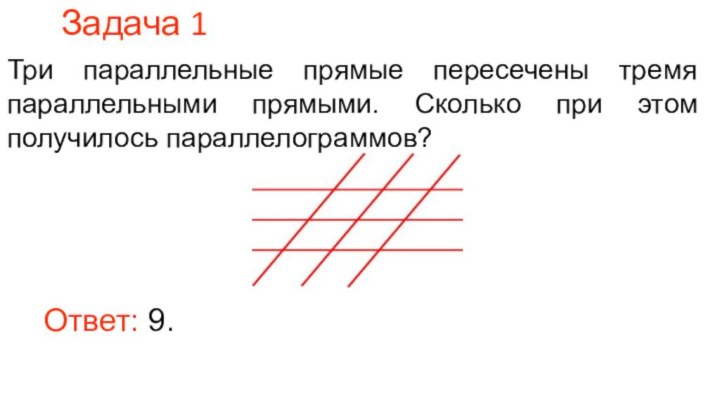
Задача 1
Три параллельные прямые пересечены тремя параллельными прямыми.
Сколько при этом получилось параллелограммов?
Ответ: 9.
Слайд 36
Задача 2
Сколько различных параллелограммов можно получить из двух
равных треугольников, прикладывая их друг к другу различным образом?
Ответ:
3.
Слайд 37
Задача 2
Сколько различных параллелограммов можно получить из двух
равных треугольников, прикладывая их друг к другу различным образом?
Ответ: 3.
Задача 3
У параллелограмма две стороны равны 10 см и 15 см. Чему равны две другие стороны?
Ответ: 10 см и 15 см
Слайд 38
Задача 2
Сколько различных параллелограммов можно получить из двух
равных треугольников, прикладывая их друг к другу различным образом?
Задача
3
У параллелограмма две стороны равны 10 см и 15 см. Чему равны две другие стороны?
Слайд 39
Задача 2
У параллелограмма две стороны равны 10 см
и 15 см. Чему равны две другие стороны?
Ответ: 10
см и 15 см.
Слайд 40
Упражнение 8
Найдите тупой угол параллелограмма, если его острый
угол равен 60о.
Ответ: 120о.
Слайд 41
Упражнение 9
Один из внешних углов параллелограмма равен 62о.
Найдите больший угол параллелограмма.
Ответ: 118о.
Слайд 42
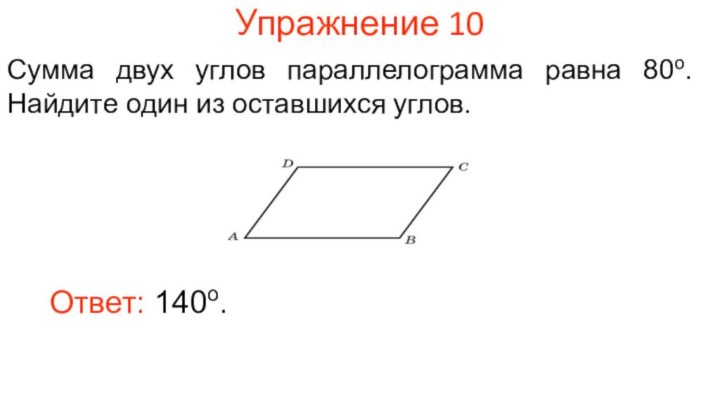
Упражнение 10
Сумма двух углов параллелограмма равна 80о. Найдите
один из оставшихся углов.
Ответ: 140о.
Слайд 43
Задача 1
Один угол параллелограмма больше другого на 40о.
Найдите больший угол.
Задача 2
Диагональ параллелограмма образует с двумя его
сторонами углы 25о и 35о. Найдите больший угол параллелограмма.
Слайд 44
Задача 1
Один угол параллелограмма больше другого на 40о.
Найдите больший угол.
Решение: пусть, тогда
∠D =х+40°, по свойству
параллелограмма получаем:
∠A+∠D=180°; х+х+40=180
2·х=180-40; 2·х=140; х=70°;
∠A=70° и ∠D =70°+40°=110°
Ответ: 70°, 110°
Слайд 45
Задача 1
Один угол параллелограмма больше другого на 40о.
Найдите больший угол.
Задача 2
Диагональ параллелограмма образует с двумя его
сторонами углы 25о и 35о. Найдите больший угол параллелограмма.
Слайд 46
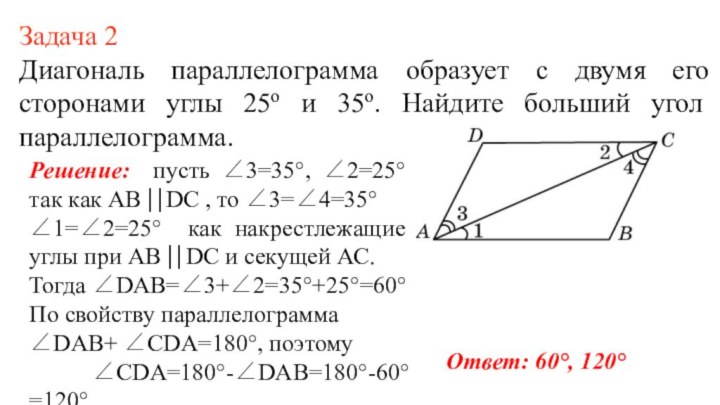
Задача 2
Диагональ параллелограмма образует с двумя его сторонами
углы 25о и 35о. Найдите больший угол параллелограмма.
Решение:
пусть ∠3=35°, ∠2=25° так как AB ⎢⎢DC , то ∠3=∠4=35°
∠1=∠2=25° как накрестлежащие углы при AB ⎢⎢DC и секущей АС.
Тогда ∠DAB=∠3+∠2=35°+25°=60°
По свойству параллелограмма
∠DAB+ ∠СDA=180°, поэтому
∠СDA=180°-∠DAB=180°-60°=120°
Ответ: 60°, 120°
Слайд 47
ЗАДАЧА В ФОРМАТЕ ОГЭ
В параллелограмме АВСD проведена биссектриса
угла А. Она разбивает сторону ВС на отрезки ВН=6
см и НС=4 см. Найдите периметр параллелограмма
Н
6см
4см
2
1
3
Решение:
Слайд 48
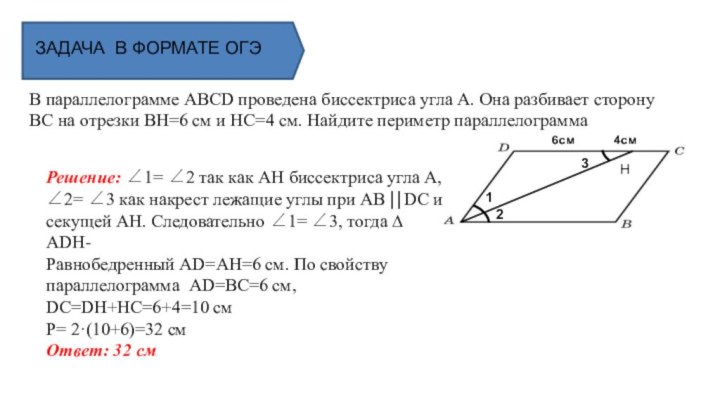
ЗАДАЧА В ФОРМАТЕ ОГЭ
В параллелограмме АВСD проведена биссектриса
угла А. Она разбивает сторону ВС на отрезки ВН=6
см и НС=4 см. Найдите периметр параллелограмма
Н
6см
4см
2
1
3
Решение: ∠1= ∠2 так как АН биссектриса угла А,
∠2= ∠3 как накрест лежащие углы при AB ⎢⎢DC и секущей АН. Следовательно ∠1= ∠3, тогда ∆ ADH-
Равнобедренный AD=AH=6 см. По свойству параллелограмма AD=ВС=6 см, DC=DН+НС=6+4=10 см
Р= 2·(10+6)=32 см
Ответ: 32 см
Слайд 49
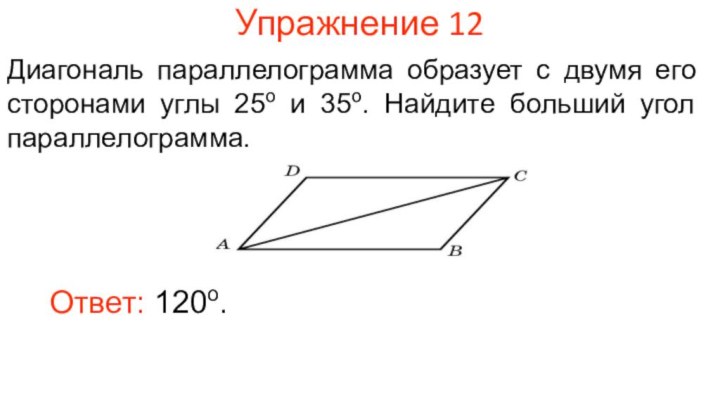
Упражнение 12
Диагональ параллелограмма образует с двумя его сторонами
углы 25о и 35о. Найдите больший угол параллелограмма.
Ответ:
120о.
Слайд 50
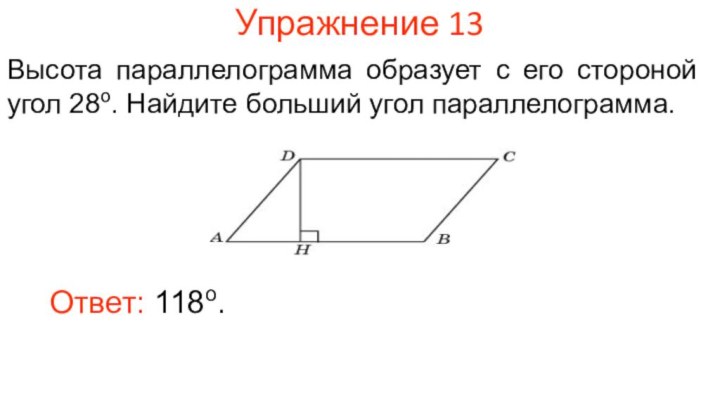
Упражнение 13
Высота параллелограмма образует с его стороной угол
28о. Найдите больший угол параллелограмма.
Ответ: 118о.
Слайд 51
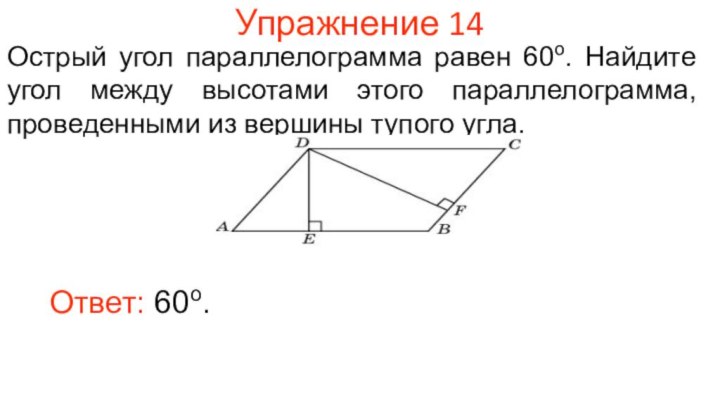
Упражнение 14
Острый угол параллелограмма равен 60о. Найдите угол
между высотами этого параллелограмма, проведенными из вершины тупого угла.
Ответ: 60о.
Слайд 52
Упражнение 15
Угол между высотами параллелограмма, проведенными из вершины
тупого угла, равен 50о. Найдите острый угол параллелограмма.
Ответ:
50о.
Слайд 53
Упражнение 16
Найдите меньший угол параллелограмма, если два его
угла относятся как 3:7.
Ответ: 54.
Слайд 54
Упражнение 17
Найдите угол между биссектрисами углов параллелограмма, прилежащими
к одной стороне.
Ответ: 90о.
Слайд 55
Упражнение 18
На рисунке ABCD – параллелограмм, BE ||
DF. Какой фигурой является четырехугольник BFDE?
Ответ: Параллелограммом.
Слайд 56
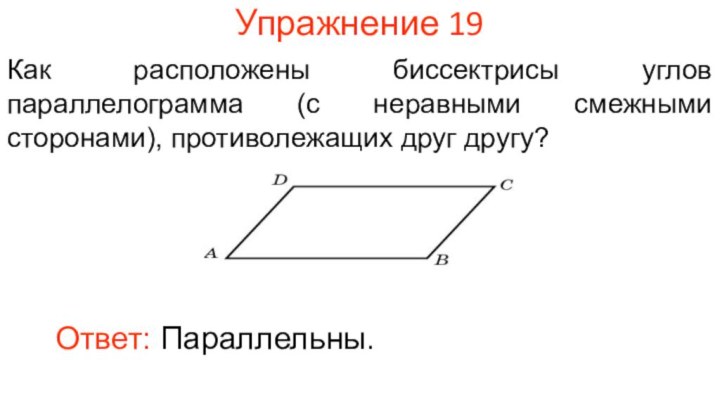
Упражнение 19
Как расположены биссектрисы углов параллелограмма (с неравными
смежными сторонами), противолежащих друг другу?
Ответ: Параллельны.
Слайд 57
Упражнение 20
Существует ли параллелограмм, в котором две стороны
и одна диагональ соответственно равны: а) 5 см,
2 см, 2 см; б) 7 см, 4 см, 11 см; в) 2 см, 3 см, 4 см; г) 3 см, 8 см, 10 см?
Ответ: а) Нет;
б) нет;
в) да;
г) да.
Слайд 58
Упражнение 21
Периметр параллелограмма равен 48 см. Найдите стороны
параллелограмма, если: а) одна сторона на 2 см больше
другой; б) разность двух сторон равна 7 см; в) одна из сторон в два раза больше другой.
Ответ: а) 11 см, 13 см, 11 см, 13 см;
б) 8,5 см, 15,5 см, 8,5 см, 15,5 см;
в) 8 см, 16 см, 8 см, 16 см.
Слайд 59
Упражнение 22
Две стороны параллелограмма относятся как 3 :
4, а периметр его равен 2,8 м. Найдите стороны
параллелограмма.
Ответ: 0,6 м, 0,8 м, 0,6 м, 0,8 м.
Слайд 60
Упражнение 23
Расстояния от точки пересечения диагоналей параллелограмма до
двух его вершин равны 3 см и 4 см.
Найдите расстояния от нее до двух других вершин?
Ответ: 3 см и 4 см.
Слайд 61
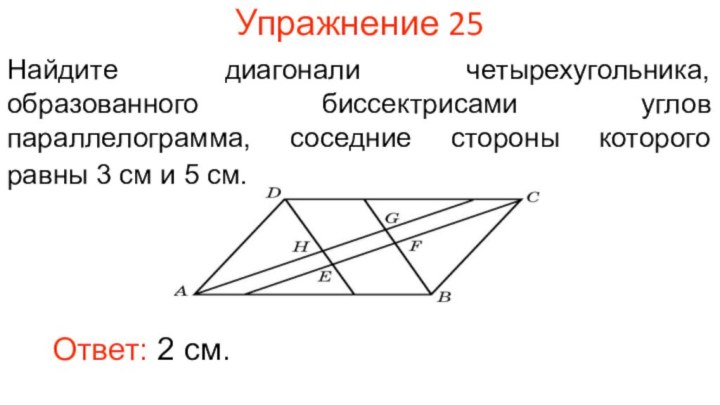
Упражнение 24
Боковая сторона равнобедренного треугольника равна 5 м.
Из точки, взятой на основании этого треугольника, проведены две
прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
Ответ: 10 м.