Слайд 2
В данной работе речь пойдёт об самом популярном
учёном, о самой загадочной личности, о человеке – символе
и человеке – фантоме, философе и пророке - это ПИФАГОР. Он был основоположником дедуктивного научного знания – математики и родоначальником многих мистических учений, учредителем религиозно-этического братства и создателем научно- философской школы, ставшей воистину союзом Истины, Добра и Красоты. Пифагор воспитал в человечестве веру в могущество разума, убеждённость в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.
Данная презентация обращена к юношеству, но будет интересна всем, кого не оставляет равнодушным великая античная культура, у колыбели которой стоял великий Пифагор.
Слайд 3
О жизни Пифагора известно немного. Он родился в
580 г. до н.э. в Древней Греции на острове
Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
ПИФАГОР САМОССКИЙ
(ОК. 580 – ОК. 500 Г. ДО Н.Э.)
Слайд 4
САМОС
На кровле он стоял высоко
И на Самос богатый
око
С весельем гордым преклонял.
«Сколь щедро взыскан я богами!
Сколь счастлив
я между царями!»
Царю Египта он сказал.
Памятник Пифагору в Самосе
(Скульптор Н. Икарис. 1989 г.)
Слайд 5
Отцом Пифагора был
Мнесарх – резчик по драгоценным камням. Имя матери Пифагора
не сохранилось.
Многие считали, что Пифагор – это не имя, а прозвище. По многим античным свидетельствам, родившийся мальчик был удивительно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей иного Пифагора были: старец Гермодамант и Ферекид Сиросский
Слайд 6
В 550 году до н. э Пифагор принимает
решение и отправляется в Египет. Итак, перед Пифагором открывается
неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям лежит через религию.
После одиннадцати лет обучения в Египте, Пифагор отправляется на Родину, где по пути попадает в Вавилонский плен.
Слайд 7
ВАВИЛОН
Вавилоняне ценили умных людей, поэтому он нашёл своё
место среди вавилонских мудрецов. Наука Вавилона была более развитой,
нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину.
Слайд 8
КРОТОН
В Кротоне начинается самый славный период в жизни
Пифагора. Там он учредил нечто вроде религиозно-этического братства или
тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни.
Слайд 9
ПИФАГОРЕЙСКАЯ ШКОЛА
Пифагор организовал религиозно-этическое братство, который впоследствии
назовут пифагорейским союзом. Члены союза должны были
придерживаться определённых принципов:
во-первых, стремиться к прекрасному и славному,
во-вторых, быть полезным,
в-третьих, стремиться к высокому наслаждению.
Слайд 10
ФРАГМЕНТ ФРЕСКИ РАФАЭЛЯ
«ПИФАГОР СРЕДИ УЧЕНИКОВ. АФИНСКАЯ ШКОЛА».
1511 Г.
Слайд 11
В ШКОЛЕ ПИФАГОРА
Пифагорейская система занятий
состояла из трёх разделов:
учения о числах – арифметике,
учения о фигурах – геометрии
учения о строении Вселенной – астрономии.
Музыка, гармония и числа были неразрывно связаны в учении Пифагорейцев. Математика и числовая мистика были фантастически перемешаны в нём.
В школе Пифагора открытия учеников приписывались учителю, поэтому практически не возможно было определить, что сделал Пифагор, а что его ученики.
Главным пифагорейским символом - символом здоровья и опознавательным знаком – была пентаграмма или пифагорейская звезда
Слайд 12
ЗАПОВЕДИ ПИФАГОРА И ЕГО УЧЕНИКОВ
Делать то, что впоследствии
не огорчит тебя и не принудит раскаиваться;
Не делай никогда
того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Слайд 13
АФОРИЗМЫ ПИФАГОРА
Прежде всего не теряй самоуважения
Делай великое, не
обещая великого
Не пренебрегай здоровьем своего тела
Прежде, чем лечь спать,
проанализируй свои поступки за день
Две вещи делают человека богоподобным: жизнь для блага общества и правдивость
Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова
Слайд 14
ТЕОРЕМА ПИФАГОРА
В настоящее время все согласны с
тем, что эта теорема не была открыта Пифагором. Она
была известна еще задолго до него. Ее знали в Китае, Вавилонии, Египте. Вернее, не ее, а частные случаи. Однако полагают, что Пифагор первым дал ее полноценное доказательство. В древности она читалась так:
Площадь квадрата, построенного на
гипотенузе прямоугольного треугольника,
равна сумме площадей квадратов,
построенных на его катетах.
Слайд 15
ТЕОРЕМА ПИФАГОРА
Хотя теорема связана с именем Пифагора, она
была известна задолго до него:
Вавилонских текстах теорема встречается за
1200 лет до Пифагора.
Треугольник со
сторонами 3, 4 и 5
часто называют египетским, т.к. он
был известен
древним египтянам
Слайд 16
Теорема Пифагора издавна широко
применялась в различных областях
жизни.
Слайд 17
СОНЕТ О ТЕОРЕМЕ ПИФАГОРА
Пребудет вечной истина, как скоро
Её
познает слабый человек!
И ныне теорема Пифагора
Верна, как и
в его далёкий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
А. Шамиссо.
Слайд 18
Характерный чертеж теоремы Пифагора, который ныне иногда превращается
школьниками, например, в облаченного в мантию профессора или человека
в цилиндре, в те времена нередко употреблялся как символ математики.
Слайд 19
ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ
Доказательство теоремы
считалось в
кругах
учащихся средних веков
очень трудным и называлось
иногда Pons asinorum-
ослиный
мост или
elefuqa-бегство убогих.
Слайд 20
ПРОСТЕЙШЕЕ ДОКАЗАТЕЛЬСТВО
Простейшее доказательство теоремы получается в простейшем случае
равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть
на мозаику равнобедренных прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
Теорема доказана.
Слайд 21
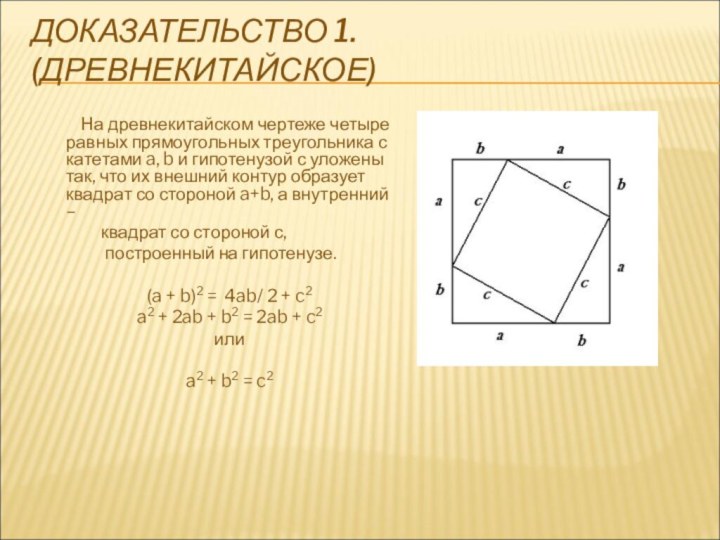
ДОКАЗАТЕЛЬСТВО 1. (ДРЕВНЕКИТАЙСКОЕ)
На
древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a,
b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний –
квадрат со стороной с,
построенный на гипотенузе.
(a + b)2 = 4ab/ 2 + c2
a2 + 2ab + b2 = 2ab + c2
или
a2 + b2 = c2
Слайд 22
ДОКАЗАТЕЛЬСТВО 2. (ДЖ. ГАРДФИЛД 1882 Г.)
Расположим два
равных прямоугольных треугольника так, чтобы катет одного из них
был продолжением другого
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту
S = (a + b)·(a + b)
2
C другой стороны, площадь трапеции равна сумме площадей полученных треугольников: S = 2ab + c2
2 2
Приравнивая данные выражения, получаем:
a2 + b2 = c2
Слайд 23
СТАРЕЙШЕЕ ДОКАЗАТЕЛЬСТВО 3. (СОДЕРЖИТСЯ В ОДНОМ ИЗ ПРОИЗВЕДЕНИЙ
БХАСКАРЫ).
Пусть АВСD квадрат, сторона которого равна гипотенузе прямоугольного треугольника
АВЕ (АВ = с, ВЕ = а, АЕ = b);
Пусть СК┴ВЕ = а, DL┴CK, AM┴DL
ΔABE = ∆BCK = ∆CDL = ∆AMD,
значит KL = LM = ME = EK = a-b.
c2 = 4ab/ 2 + (a – b)2
c2 = 2ab + a2 – 2ab +b2
c2 = a2 + b2
Слайд 24
ДОКАЗАТЕЛЬСТВО 4.
Квадрат со стороной (a+b), можно разбить на
части либо как на рисунке а), либо как на
рисунке b). Ясно, что треугольники на обоих рисунках одинаковы. А если от равных (площадей) отнять равные, то и останутся равные.
Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали лишь одним словом: Смотри!
ЕВКЛИДА
В течение двух тысячелетий наиболее распространенным доказательством
теоремы Пифагора было придуманное Евклидом.
Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.
Слайд 26
Суть истины вся в том, что нам она
– навечно,
Когда хоть раз в прозрении её увидим свет,
И
теорема Пифагора через столько лет
Для нас. Как для него, бесспорна, безупречна…
(Отрывок из стихотворения А. Шамиссо)
ЗАКЛЮЧЕНИЕ
Мы изучили ряд исторических
и математических источников, в том числе информацию в Интернете, и увидели, что теорема Пифагора интересна не только своей историей, но и тем, что она занимает важное место в жизни и науке. Об этом свидетельствуют приведённые нами в данной работе различные трактовки текста этой теоремы и пути её доказательства.
Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.
Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор – замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Он вполне может служить примером для нас, далёких потомков.