- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Теория по планиметрии (проектная работа)
Содержание
- 2. Цель работы:подготовка к успешному выполнению заданий С4
- 3. Геометрия является самым могущественным средством для изощрения
- 4. В математике следует понимать не формулы ,
- 5. ВведениеС о д е р ж а
- 6. Методы, используемые в работе для решения задачгеометрический(требуемое
- 7. Чтоб мудро жизнь прожить Знать надобно немало
- 8. Симметрия является той идеей, с помощью которой
- 9. Геометрия есть познание всего сущего.
- 10. Мало иметь хороший ум, главное – хорошо
- 11. Вдохновение нужно в геометрии не меньше, чем
- 12. Лучший способ изучить что-либо - это открыть
- 13. Величие человека - в его способности мыслить.
- 14. Если вы хотите научиться плавать, то смело
- 15. Геометрия полна приключений, потому что за каждой
- 16. Глава 10. Пересекающиеся окружностиПри решении задач по
- 17. Трудность решения в какой-то мере входит в
- 18. Математика уступает свои крепости лишь сильным и
- 19. Доказательство - это рассуждение, которое убеждает.
- 20. Рано или поздно всякая правильная математическая идея
- 21. Между духом и материей посредничает математика.
- 22. Если тебе трудно сразу понять всю бесконечность,
- 23. Тот, кто не знает математики, не может
- 24. Скачать презентацию
- 25. Похожие презентации











Слайд 2
Цель работы:
подготовка к успешному выполнению заданий С4
Задачи:
Способствовать
формированию осознанных мотивов изучения геометрии
методы и приемы при решении типовых заданий
Слайд 3
Геометрия является самым могущественным средством для изощрения наших
умственных способностей и дает нам возможность правильно мыслить и
рассуждать. Г. ГалилейАктуальность темы:
выявить общие подходы при решении задач по планиметрии, используя необходимый теоретический материал для успешного решения задачи С-4 на ЕГЭ
углубить свои знания по геометрии
Слайд 4 В математике следует понимать не формулы , а
процесс мышления
Е. И. ИгнатьевСтруктура работы :
Работа состоит из 14 глав, рассматриваются общие подходы к решению геометрических задач, при обилии их различных типов и многообразии их приемов и методов решения
Слайд 5
Введение
С о д е р ж а н
и е
Необходимые теоретические знания по планиметрии при решении задания
С4Глава 1. Медиана прямоугольного треугольника
Глава 2. Удвоение медианы
Глава 3. Параллелограмм. Средняя линия треугольника
Глава 4. Трапеция
Глава 5. Нахождение высот треугольника
Глава 6. Отношение отрезков
Глава 7. Отношение площадей
Глава 8. Касательная к окружности
Глава 9. Касающиеся окружности
Глава 10. Пересекающиеся окружности
Глава 11. Окружности, связанные с треугольником и четырехугольником
Глава 12. Пропорциональные отрезки в окружности
Глава 13. Углы, связанные с окружностью. Метод вспомогательной окружности
Глава 14. Подобные треугольники
Заключение
Список литературы
Слайд 6
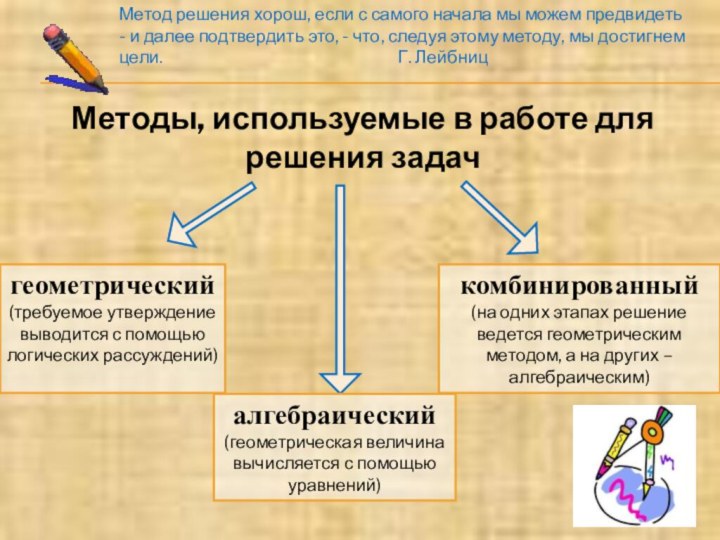
Методы, используемые в работе для решения задач
геометрический
(требуемое утверждение
выводится с помощью логических рассуждений)
алгебраический
(геометрическая величина вычисляется с помощью
уравнений)комбинированный
(на одних этапах решение ведется геометрическим методом, а на других – алгебраическим)
Метод решения хорош, если с самого начала мы можем предвидеть - и далее подтвердить это, - что, следуя этому методу, мы достигнем цели. Г. Лейбниц
Слайд 7
Чтоб мудро жизнь прожить
Знать надобно немало
О. Хаям
Глава 1. Медиана прямоугольного треугольника
При решении задач этой главы используются следующие свойства:
1. Медиана прямоугольного треугольника, проведенная из вершины прямого угла . Равна половине гипотенузы.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный
Слайд 8 Симметрия является той идеей, с помощью которой человек
веками пытается объяснить и создать порядок, красоту и совершенство.
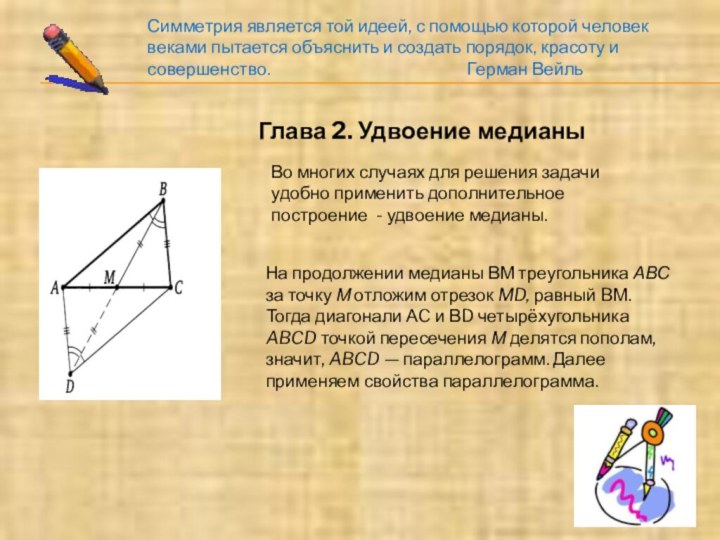
Герман ВейльГлава 2. Удвоение медианы
Во многих случаях для решения задачи удобно применить дополнительное построение - удвоение медианы.
На продолжении медианы ВМ треугольника АВС за точку М отложим отрезок MD, равный BМ. Тогда диагонали АC и ВD четырёхугольника ABCD точкой пересечения М делятся пополам, значит, ABCD — параллелограмм. Далее применяем свойства параллелограмма.
Слайд 9
Геометрия есть познание всего сущего.
Платон
Глава 3. Параллелограмм. Средняя линия треугольника
Для решения задач этого раздела нужно знать :
свойства и признаки параллелограмма;
теорему о медианах треугольника (медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника);
теорему о средней линии треугольника;
Свойство : сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон;
Середины сторон любого четырёхугольника являются вершинами параллелограмма.
А
В
С
D
Слайд 10 Мало иметь хороший ум, главное – хорошо его
применять.
Р. ДекартГлава 4. Трапеция
Ещё одно важное свойство трапеции - точка пересечения диагоналей любой трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
При решении задач на трапецию во многих случаях полезны дополнительные построения, связанные с параллельным переносом боковой стороны или диагонали.
При решении задач, связанных с равнобедренной трапецией, кроме общеизвестных свойств и признаков (углы при основании равны, диагонали равны и образуют равные углы с основанием и т. д.) иногда полезно применить следующее свойство:
2AM=AD-BC
AK=0,5(AD+BC)
Слайд 11 Вдохновение нужно в геометрии не меньше, чем в
поэзии.
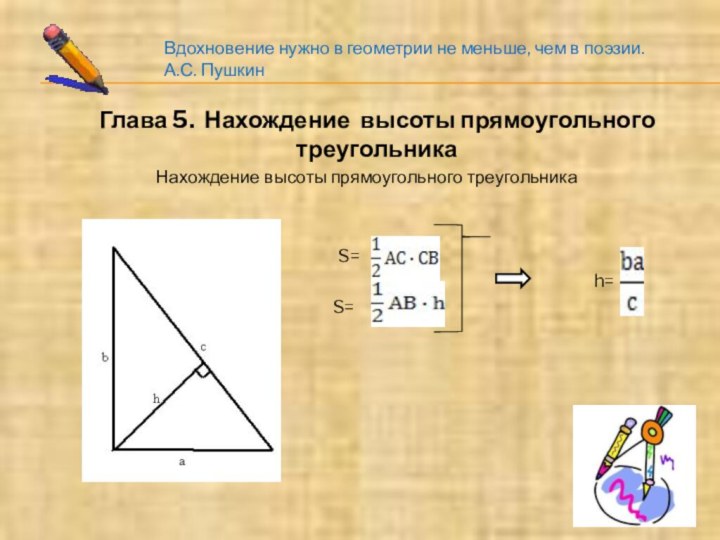
А.С. ПушкинГлава 5. Нахождение высоты прямоугольного треугольника
Нахождение высоты прямоугольного треугольника
S=
S=
h=
Слайд 12
Лучший способ изучить что-либо - это открыть самому.
Д. Пойа
Глава 6. Отношение отрезков
Задачи этой главы решаются с помощью дополнительного построения, которое приводит к подобным треугольникам.
Пример. Дан треугольник АВС. На продолжении стороны АС за точку С взята точка N, причём АС = 2CN. Точка М находится на стороне ВС, причём ВМ : МС =1 : З. В каком отношении прямая MN делит сторону АВ?
Решение.
Через точку В проведём прямую, параллельную АС. Пусть прямая MN пересекает её в точке Т, а прямую АВ - в точке К.
Обозначим АС = а. Тогда CN = 0,5а, AN=1,5a. Из подобия треугольников ТВМ и NCM нахом, что
ТВ=1/3СN=1/6a.
Из подобия треугольников ТВК и NAK –
ВК:АК=ТВ:AN=1/9.
Ответ:
1: 9, считая от точки В.
Слайд 13
Величие человека - в его способности мыслить.
Б. Паскаль
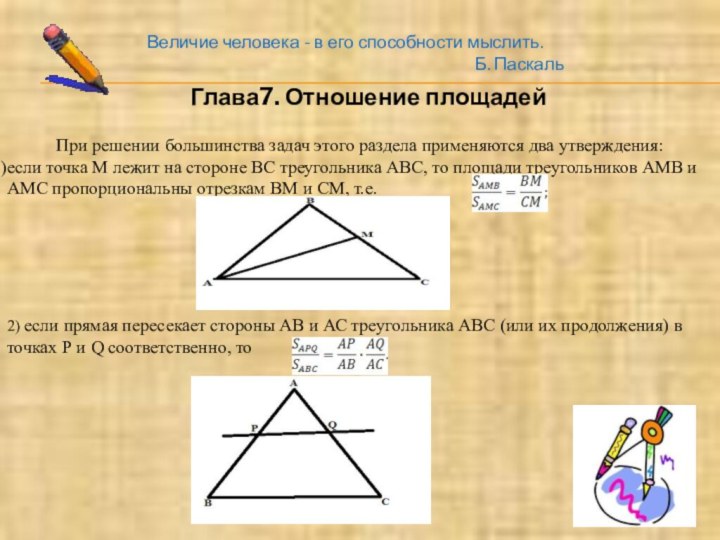
Глава7. Отношение площадей
При решении большинства задач этого раздела применяются два утверждения:
если точка М лежит на стороне ВС треугольника АВС, то площади треугольников АМВ и АМС пропорциональны отрезкам ВМ и СМ, т.е.
2) если прямая пересекает стороны АВ и АС треугольника АВС (или их продолжения) в точках Р и Q соответственно, то
Слайд 14 Если вы хотите научиться плавать, то смело входите
в воду, а если хотите научиться решать задачи, то
решайте их!Д. Пойа
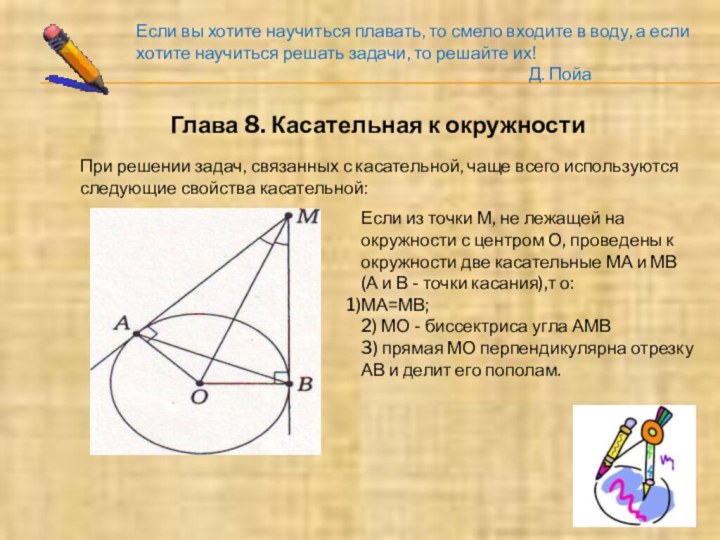
Глава 8. Касательная к окружности
При решении задач, связанных с касательной, чаще всего используются следующие свойства касательной:
Если из точки М, не лежащей на окружности с центром О, проведены к окружности две касательные МА и МВ
(А и В - точки касания),т о:
МА=МВ;
2) МО - биссектриса угла АМВ
3) прямая МО перпендикулярна отрезку АВ и делит его пополам.
Слайд 15 Геометрия полна приключений, потому что за каждой задачей
скрывается приключение мысли. Решить задачу – это значит пережить
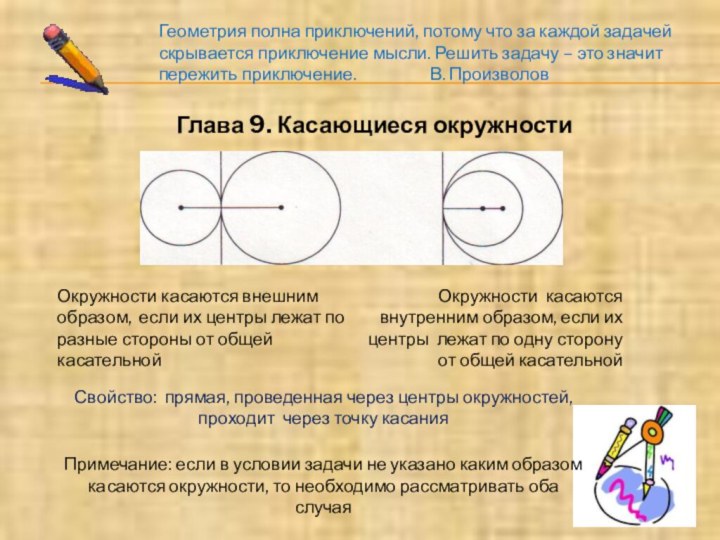
приключение. В. ПроизволовГлава 9. Касающиеся окружности
Окружности касаются внешним образом, если их центры лежат по разные стороны от общей касательной
Окружности касаются внутренним образом, если их центры лежат по одну сторону от общей касательной
Свойство: прямая, проведенная через центры окружностей, проходит через точку касания
Примечание: если в условии задачи не указано каким образом касаются окружности, то необходимо рассматривать оба случая
Слайд 16
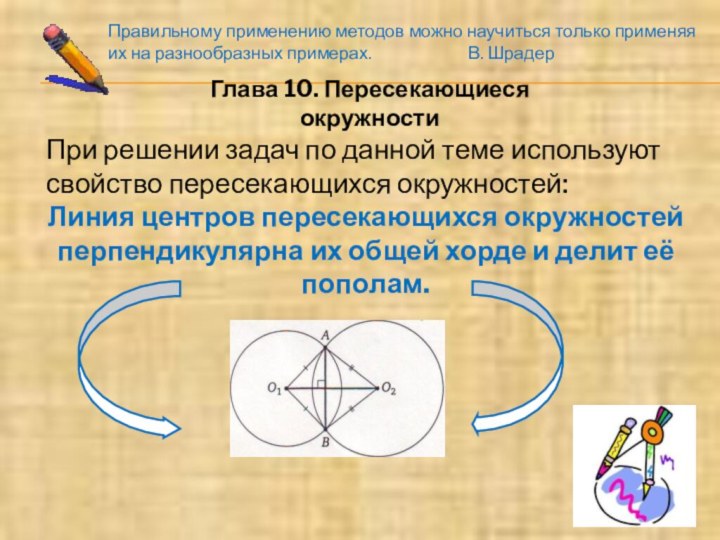
Глава 10. Пересекающиеся окружности
При решении задач по данной
теме используют свойство пересекающихся окружностей:
Линия центров пересекающихся окружностей перпендикулярна
их общей хорде и делит её пополам.Правильному применению методов можно научиться только применяя их на разнообразных примерах. В. Шрадер
Слайд 17 Трудность решения в какой-то мере входит в само
понятие задачи: там, где нет трудности, нет и задачи.
Д. Пойа
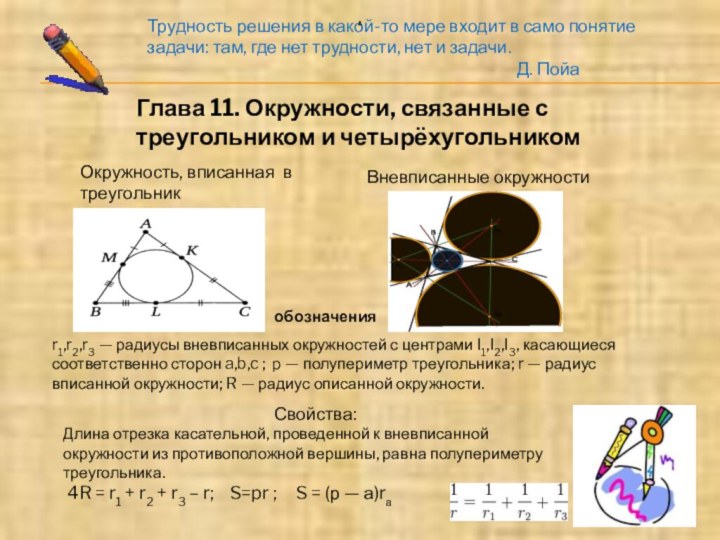
Глава 11. Окружности, связанные с треугольником и четырёхугольником
.
Окружность, вписанная в треугольник
Вневписанные окружности
обозначения
r1,r2,r3 — радиусы вневписанных окружностей с центрами I1,I2,I3, касающиеся соответственно сторон a,b,c ; p — полупериметр треугольника; r — радиус вписанной окружности; R — радиус описанной окружности.
Свойства:
Длина отрезка касательной, проведенной к вневписанной окружности из противоположной вершины, равна полупериметру треугольника.
4R = r1 + r2 + r3 – r; S=pr ; S = (р — а)rа
Слайд 18
Математика уступает свои крепости лишь сильным и смелым.
А.П. Конфорович
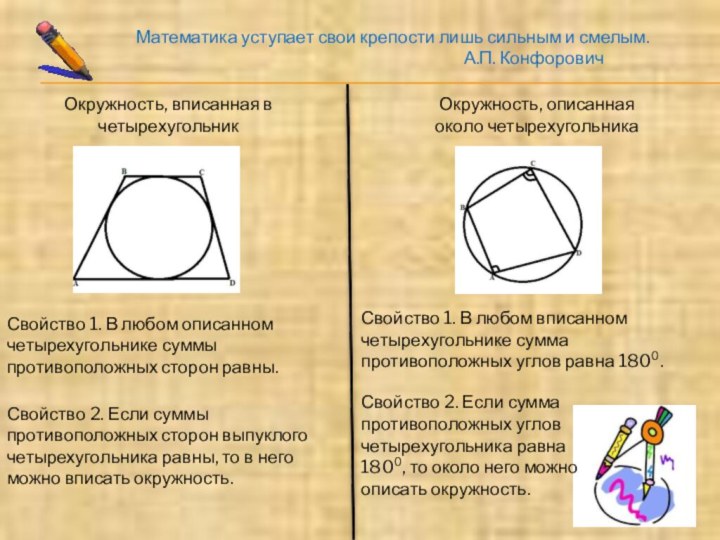
Окружность, вписанная в четырехугольник
Окружность, описанная около четырехугольника
Свойство 1. В любом описанном четырехугольнике суммы противоположных сторон равны.
Свойство 2. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Свойство 1. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Свойство 2. Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
Слайд 19
Доказательство - это рассуждение, которое убеждает.
Ю.А. Шиханович
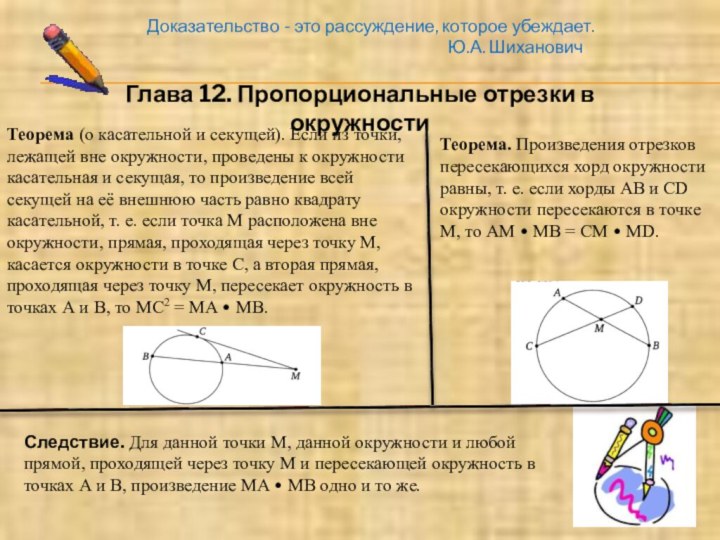
Глава 12. Пропорциональные отрезки в окружности
Теорема. Произведения отрезков пересекающихся хорд окружности
равны, т. е. если хорды АВ и CD окружности пересекаются в точке М, то АМ • МВ = СМ • MD.
Теорема (о касательной и секущей). Если из точки, лежащей вне окружности, проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной, т. е. если точка М расположена вне окружности, прямая, проходящая через точку М, касается окружности в точке С, а вторая прямая, проходящая через точку М, пересекает окружность в точках А и В, то МС2 = МА • МВ.
Следствие. Для данной точки М, данной окружности и любой прямой, проходящей через точку М и пересекающей окружность в точках А и В, произведение МА • МВ одно и то же.
Слайд 20 Рано или поздно всякая правильная математическая идея находит
применение в том или ином деле.
А.Н. КрыловГлава 13. Углы, связанные с окружностью. Метод
вспомогательной окружности
Вписанный угол равен половине угловой величины соответствующего центрального угла (дуги).
Вписанные углы, опирающиеся на одну и ту же дугу, равны, т. е. если точки А и В лежат на окружности по одну сторону от прямой, содержащей хорду CD, то
LCAD = LCBD.
Если же точки А и В лежат по разные стороны от прямой CD, то
LCAD + LCBD =180°.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Угловая величина дуги - это угловая величина соответствующего этой дуге центрального угла.
Слайд 21
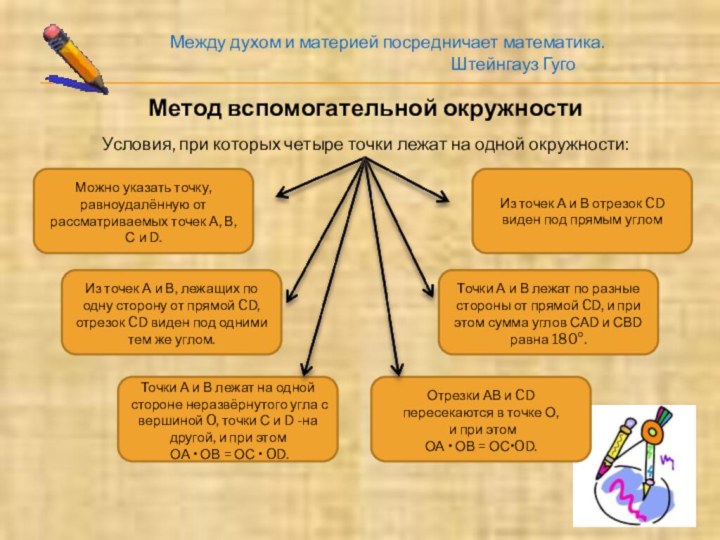
Между духом и материей посредничает математика.
Штейнгауз Гуго
Условия, при которых четыре точки лежат на одной окружности:
Метод вспомогательной окружности
Можно указать точку, равноудалённую от рассматриваемых точек А, В, С и D.
Из точек А и В, лежащих по одну сторону от прямой CD, отрезок CD виден под одними тем же углом.
Отрезки АВ и CD пересекаются в точке О,
и при этом
ОА • ОВ = ОС•OD.
Точки А и В лежат на одной стороне неразвёрнутого угла с вершиной O, точки С и D -на другой, и при этом
ОА • ОВ = ОС • OD.
Точки А и В лежат по разные стороны от прямой CD, и при этом сумма углов САD и СВD равна 180°.
Из точек А и В отрезок CD виден под прямым углом
Слайд 22 Если тебе трудно сразу понять всю бесконечность, постарайся
понять ее хотя бы наполовину.
Врублевский Славомир Глава 14. Вспомогательные подобные треугольники
При решении задач этой главы ключевая идея состоит в отыскании пары подобных треугольников.
Пример. На стороне АВ треугольника АВС отмечена точка D, причём
LBCD = LBAC. Известно, что ВС = а, АС =b, АВ = с. Найдите CD.
Решение.
Треугольники CBD и АВС подобны по двум углам,т. к. LBCD = LBAC по условию, а угол при вершине В —общий. Значит, соответствующие стороны этих треугольников пропорциональны,
т.е. СD: АС=ВС:АВ. Следовательно,
CD=
Ответ:
Слайд 23 Тот, кто не знает математики, не может узнать
никакой другой науки и даже не может обнаружить своего
невежества . Роджер БэконЗаключение
Надеюсь, что рассмотренные теоретические вопросы и решенные задачи помогут не только мне, но и другим обучающимся, заинтересовавшимся моей работой, в успешном решении задания С4 при выполнении ЕГЭ по математике.
Желаю удачи
в изучении геометрии !