Презентация на тему Три кита геометрии

работы – познакомиться с данными признаками, с их особенностями.

Узнать где и как в жизни применяются компьютеры.

Немного о проекте

треугольник, как ты прекрасен.
Как красив и богат,
Ибо ты имеешь

три стороны.
Три угла, три вершины.
Ты один можешь быть:
И равнобедренным, и равносторонним,
И прямоугольным…
Ибо ты могуч…
…По тебе судят теоремы,
Тебе посвятили три признака равенства.
Ведь, чтобы доказать, что ты равен,
Нужно приложить силы.

Слово о треугольнике

стороны и угол между ними одного тр-ка равны соответственно

двум сторонам и углу между ними другого тр-ка,то такие тр-ки равны..

первый признак равенства тр-ов

<А=<А1
АВ=А1В1
АС=А1В1
Док-ть, что тр.АВС=тр.А1В1С1
Док-во:
Пусть трА1В2С2=трАВС с вершиной В2 на луче А1В1 и вершиной С2( где лежит вершина С1)
Т.к.А1В1=А1В2 верщина В2 совпадает с вершиной В1.
Т.к <В1А1С1= <В2А1С2, то луч А1С2 совпадает с лучом А1С1.
Т.к А1С1=А1С2, то вершина С2 совпадает с вершиной С1.
Следовательно, тр.А1В1С1 совпадает с тр.А1В2С2,значит тр А1В1С1=тр.АВС
Теорема доказана.

Доказательство.

словам “сторона” и “угла”
И пред ваши очи вмиг
Второй признак

подбежит.
по стороне и двум прилежащим к ней углам.
Теорема : если сторона и прилежащие к ней стороны одного тр-ка равны соответственно стороне и прилежащим к ней углам другого тр-ка, то такие тр-ки равны.

второй признак равенства тр-ов.

Доказательство:
Пусть трА1В2С2=трАВС, с вершиной В2 на луче А1В1 и Вершиной С2 в той же полуплоскости.
Т.К. А1В2=А1В1, то вершина В2 совпадает с вершиной В1.
Т.К <В1А1С2=<В1А1С1, то луч В1С2 совпадает с лучим В1С1.
Следовательно вершина С2 совпадает с вершиной С1.
Значит, трА1В1С1 совпадает с трА1В2С2, трА1В1С1=АВС.
Теорема доказана.

Доказательство 2-го признака

равны соответственно сторонам другого тк-ка, то такие тр-ки равны.
Третий

признак равенства тр-ов.

трАВС и тра1В1С1
А1В1=АВ
С1А1=СА
В1С1=ВС
Док-то, что трАВС=трА1В1С1.
Доказательство:
Допустим, тр-ки не равны. Тогда у них <А=\<А1, <В=\ <В1, <С=\<С1/
Пусть А1В1С2 – тр-к, у которого вершина С2 лежит в одной полуплоскости с вершиной С1.
Пусть Д-середина отрезка С1С2.тр-ки А1С1С2 и В1С1С2-равнобедренные с общим основанием С1С2.поэтому их медианы А1Д и В1Д-высоты. Значит, прямые А1Д и В1Д-перпендикулярны прямой С1С2. Прямые А1Д и В1Д не совпадают, т.к. т.А1,тВ1,тД не лежат на одной прямой. Но через тД можно провести одну пер-ую прямую. Мы пришли к противоречию.
Теорема доказана.

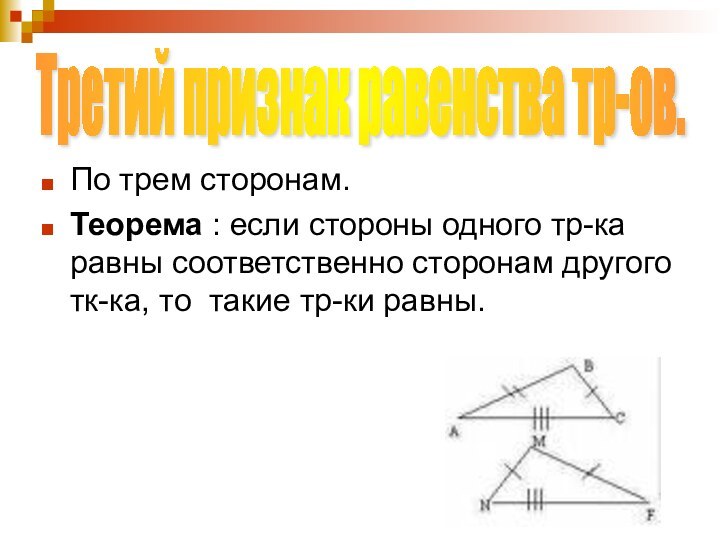
Доказательство 3-го признака равенства.

Треугольники, как

выяснилось, достаточно популярны в повседневной жизни. Мы их может встретить повсюду: в виде предупреждающих знаков, детских погремушек, треугольников самураев, Бермудского треугольника.

Использование тр-ов в жизни

ряд особенностей, которые помогают решать задачи, да и не

только их, они помогают ориентироваться в жизни.
Цель, которая была задана в начале работы, успешно достигнута.

Подведем итоги.