- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Многоугольники (подготовка к ЕГЭ)
Содержание
- 2. «Каждая решённая мною задача становилась образцом, который служил впоследствии для решения других задач»
- 3. Задача 1.В прямоугольнике ABCD опущен перпендикуляр BK
- 4. ABCMNKDII способ. Векторный метод и подобиеP∆CPN~∆AKB ⇒M – середина AK, значит, AM=MK=PC.Следовательно, MP=KC.
- 5. ABCMNKDPIII способПрименение тригонометрииУбедимся, что Пусть ∠ACB =∠ABK
- 6. ABCMNKDPIV способТригонометрия и подобиеПусть ∠ACB =∠ABK =α∆BKC:∆
- 7. V способ. Подобие и вспомогательная окружностьABCMNKD∆BDC ~∆BAKИз
- 8. VI способ.Обратный ходABCMKDPПредположим, что ∠BMN - прямой,
- 9. VII способ.
- 10. Задача №2Точка E – середина стороны AD
- 11. OABCDE1) Пусть OE = x 34∆
- 12. Задача 3В трапеции ABCD BC и AD
- 13. DCBAPNBN =NA=NPN – центр окружности, описанной около
- 14. DCBAPN68
- 15. Задача №4В равнобедренной трапеции ABCD точки M
- 16. ABCDMNPK1313188H∆BPM~∆NPA∆PMK~∆AMDОтвет: b) Найдите площадь четырехугольника PMKN, если известно, что BC = 8, AD = 18, AB=CD=13.
- 17. Задача №5.В выпуклом четырехугольнике ABCD диагонали AC
- 18. ANDKCBO13151024HANKD - прямоугольникABCD - трапецияПусть NB =
- 19. Задача №6В четырехугольнике ABCD биссектриса угла C
- 20. ADMKBCO60⁰32BK = AB =3, AM=KC=2, AD =5∆ABO:∆ADO:(2)
- 21. Скачать презентацию
- 22. Похожие презентации








Слайд 2 «Каждая решённая мною задача становилась образцом, который служил
впоследствии для решения других задач»
Слайд 3
Задача 1.
В прямоугольнике ABCD опущен перпендикуляр BK на
диагональ AC. Точки M и N – середины отрезков
AK и CD соответственно. Докажите, что угол BMN – прямой.Решение.
I способ
Векторный метод
A
B
C
D
M
N
K
высота, проведенная из вершины прямого угла
Слайд 4
A
B
C
M
N
K
D
II способ.
Векторный метод и подобие
P
∆CPN~∆AKB ⇒
M –
середина AK, значит, AM=MK=PC.
Следовательно, MP=KC.
Слайд 5
A
B
C
M
N
K
D
P
III способ
Применение тригонометрии
Убедимся, что
Пусть ∠ACB =∠ABK =α,
CN =a, AB = 2a
MP=KC, PN = 0,5BK
∆ABK:
∆ABC:
∆BCN:
∆BMK:
∆BKC:
∆MPN :
⇒∠BMN – прямой.
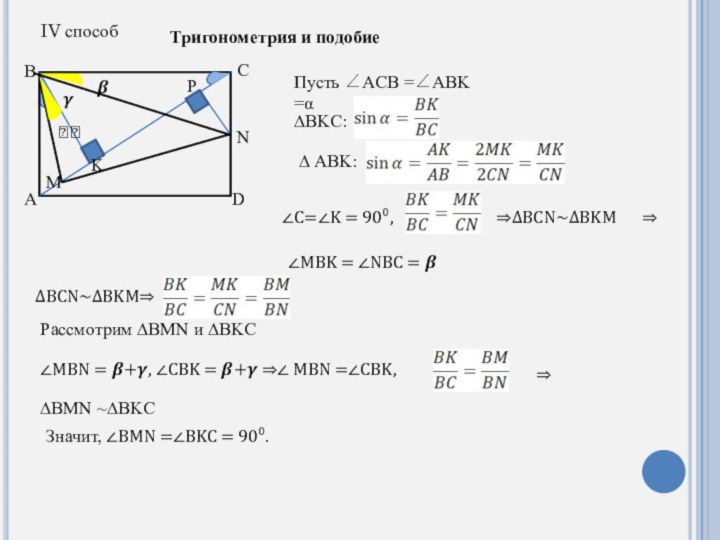
Слайд 6
A
B
C
M
N
K
D
P
IV способ
Тригонометрия и подобие
Пусть ∠ACB =∠ABK =α
∆BKC:
∆ ABK:
∠C=∠K = 90⁰,
⇒∆BCN~∆BKM
⇒
∠MBK = ∠NBC = ?
∆BCN~∆BKM⇒
?
?
?
Рассмотрим ∆BMN
и ∆BKC∠MBN = ?+?, ∠CBK = ?+? ⇒∠ MBN =∠CBK,
⇒
∆BMN ~∆BKC
Значит, ∠BMN =∠BKC = 90⁰.
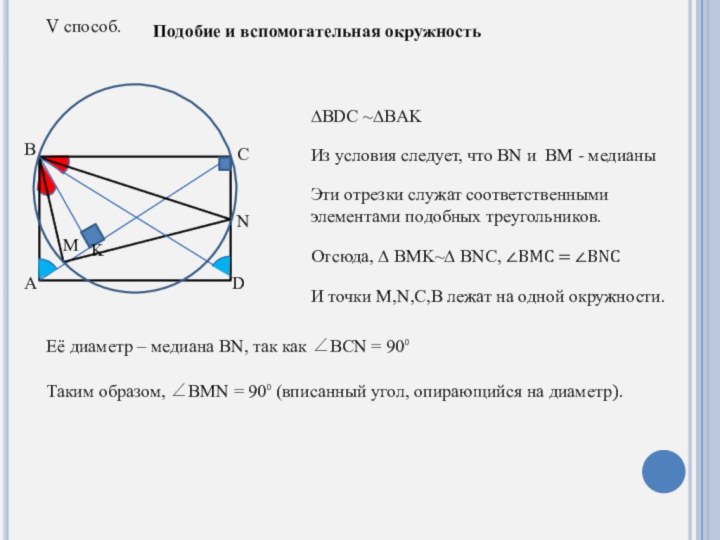
Слайд 7
V способ.
Подобие и вспомогательная окружность
A
B
C
M
N
K
D
∆BDC ~∆BAK
Из условия
следует, что BN и BM - медианы
Эти отрезки служат
соответственными элементами подобных треугольников.Отсюда, ∆ BMK~∆ BNC, ∠BMC = ∠BNC
И точки M,N,C,B лежат на одной окружности.
Её диаметр – медиана BN, так как ∠BCN = 90⁰
Таким образом, ∠BMN = 90⁰ (вписанный угол, опирающийся на диаметр).
Слайд 8
VI способ.
Обратный ход
A
B
C
M
K
D
P
Предположим, что ∠BMN - прямой, тогда
1)
2)
3)
N
4) MP = KC, MK = PC
Таким
образом, -верно, т. к. ∆PCN - прямоугольный
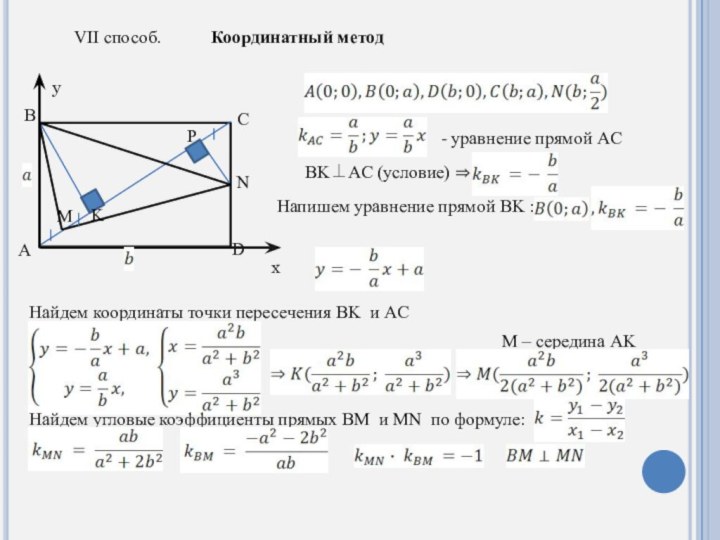
Слайд 9 VII способ. Координатный
метод
A
B
C
M
K
D
P
N
x
y
- уравнение прямой AC BK⊥AC (условие) ⇒
Напишем уравнение прямой BK :
Найдем координаты точки пересечения BK и AC
M – середина AK
Найдем угловые коэффициенты прямых BM и MN по формуле:
Слайд 10
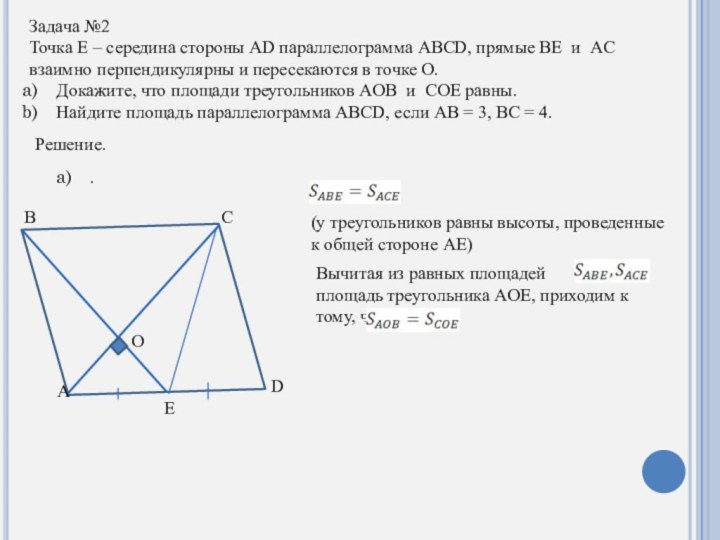
Задача №2
Точка E – середина стороны AD параллелограмма
ABCD, прямые BE и AC взаимно перпендикулярны и пересекаются
в точке O.Докажите, что площади треугольников AOB и COE равны.
Найдите площадь параллелограмма ABCD, если AB = 3, BC = 4.
Решение.
O
A
B
C
D
E
(у треугольников равны высоты, проведенные к общей стороне AE)
Вычитая из равных площадей
площадь треугольника AOE, приходим к тому, что и
.
Слайд 11
O
A
B
C
D
E
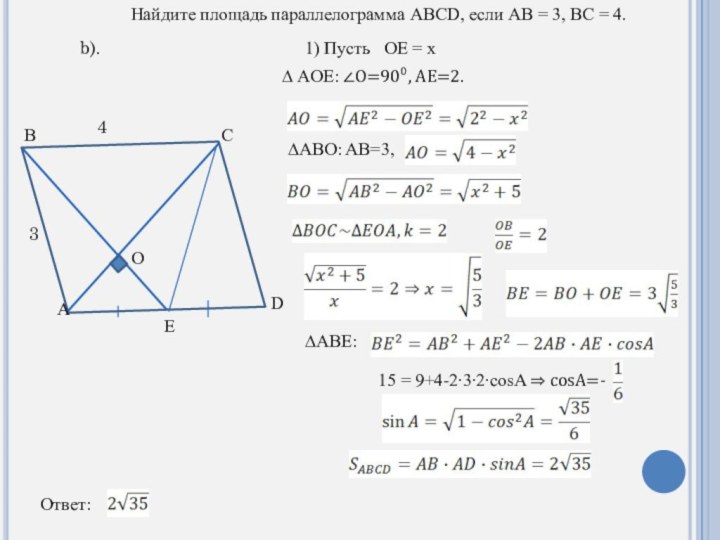
1) Пусть OE = x
3
4
∆ AOE:
∠O=90⁰, AE=2.
∆ABO: AB=3,
⇒
∆ABE:
15 =
9+4-2∙3∙2∙cosA ⇒ cosA=-Ответ:
b).
Найдите площадь параллелограмма ABCD, если AB = 3, BC = 4.
Слайд 12
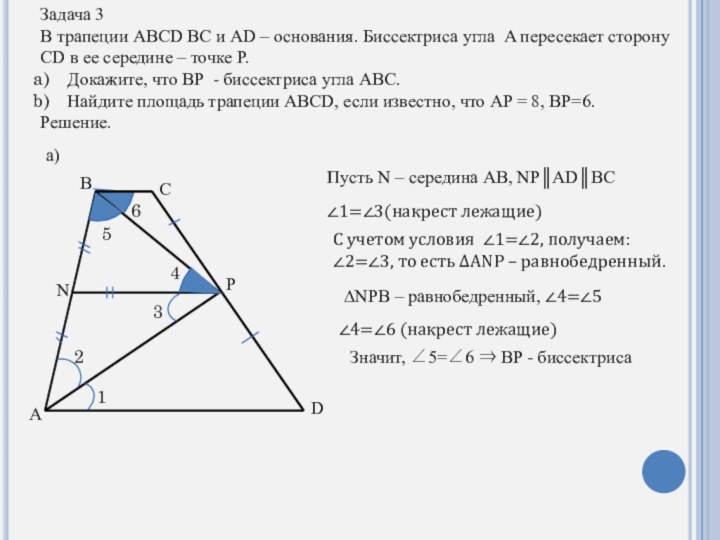
Задача 3
В трапеции ABCD BC и AD –
основания. Биссектриса угла A пересекает сторону CD в ее
середине – точке P.Докажите, что BP - биссектриса угла ABC.
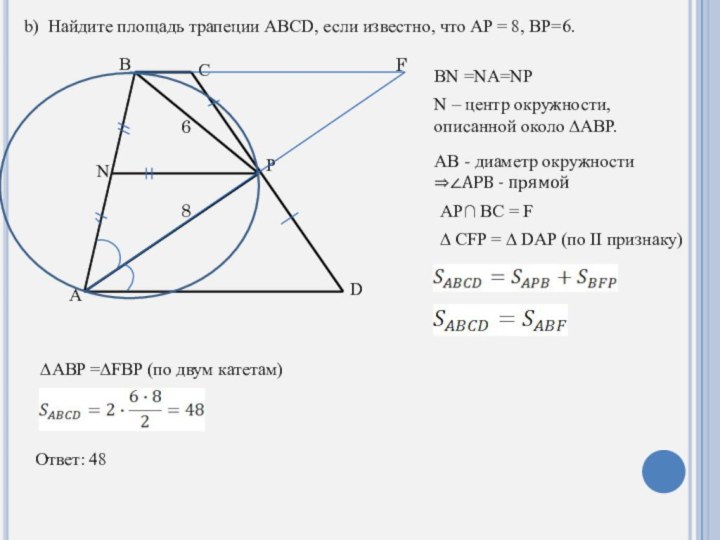
Найдите площадь трапеции ABCD, если известно, что AP = 8, BP=6.
Решение.
D
C
B
A
P
N
1
2
3
4
5
6
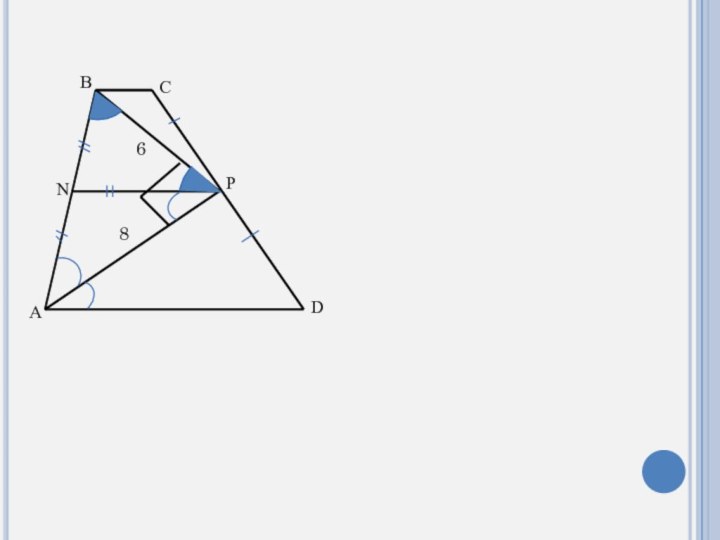
Пусть N – середина AB, NP║AD║BC
∠1=∠3(накрест лежащие)
С учетом условия ∠1=∠2, получаем: ∠2=∠3, то есть ∆ANP – равнобедренный.
∆NPB – равнобедренный, ∠4=∠5
∠4=∠6 (накрест лежащие)
Значит, ∠5=∠6 ⇒ BP - биссектриса
a)
Слайд 13
D
C
B
A
P
N
BN =NA=NP
N – центр окружности,
описанной около ∆ABP.
AB - диаметр окружности
⇒∠APB - прямой
AP∩ BC =
FF
∆ CFP = ∆ DAP (по II признаку)
∆ABP =∆FBP (по двум катетам)
6
8
Ответ: 48
b) Найдите площадь трапеции ABCD, если известно, что AP = 8, BP=6.
Слайд 15
Задача №4
В равнобедренной трапеции ABCD точки M и
N- середины оснований BC и AD соответственно. Отрезки AM
и BN пересекаются в точке P, а отрезки DM и CN пересекаются в точке K.Докажите, что площадь четырехугольника PMKN равна сумме площадей треугольников ABP и DCK.
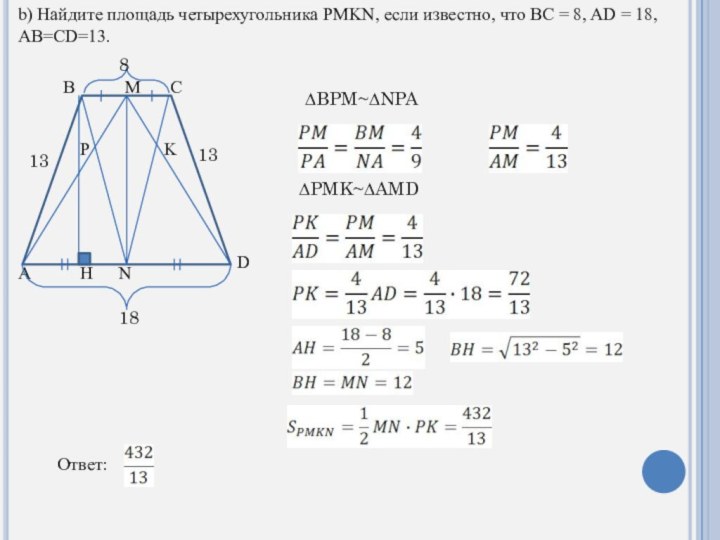
Найдите площадь четырехугольника PMKN, если известно, что BC = 8, AD = 18, AB=CD=13.
Решение.
A
B
C
D
M
N
P
K
(у треугольников равны высоты, проведенные к общей стороне BM)
Вычитая из равных площадей
приходим к тому, что
Аналогично доказываем, что
a)
Слайд 16
A
B
C
D
M
N
P
K
13
13
18
8
H
∆BPM~∆NPA
∆PMK~∆AMD
Ответ:
b) Найдите площадь четырехугольника PMKN, если известно,
что BC = 8, AD = 18, AB=CD=13.
Слайд 17
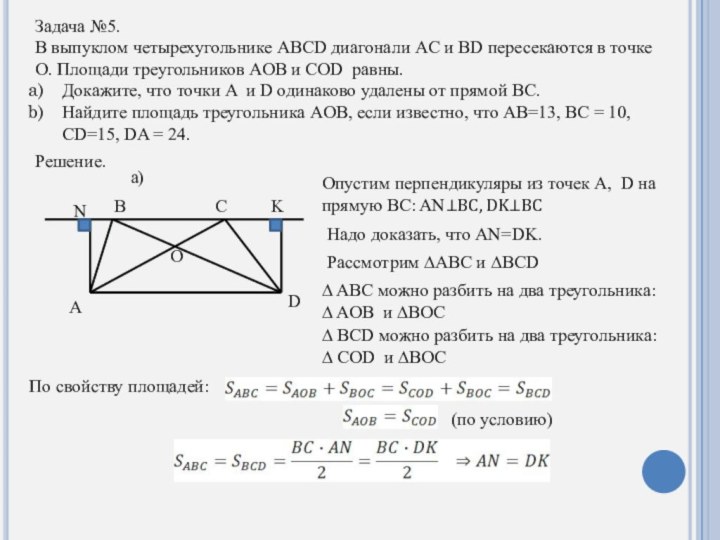
Задача №5.
В выпуклом четырехугольнике ABCD диагонали AC и
BD пересекаются в точке O. Площади треугольников AOB и
COD равны.Докажите, что точки A и D одинаково удалены от прямой BC.
Найдите площадь треугольника AOB, если известно, что AB=13, BC = 10, CD=15, DA = 24.
Решение.
A
N
D
K
C
B
O
Опустим перпендикуляры из точек A, D на прямую BC: AN⊥BC, DK⊥BC
Надо доказать, что AN=DK.
Рассмотрим ∆ABC и ∆BCD
∆ ABC можно разбить на два треугольника:
∆ AOB и ∆BOC
∆ BCD можно разбить на два треугольника:
∆ COD и ∆BOC
По свойству площадей:
(по условию)
a)
Слайд 18
A
N
D
K
C
B
O
13
15
10
24
H
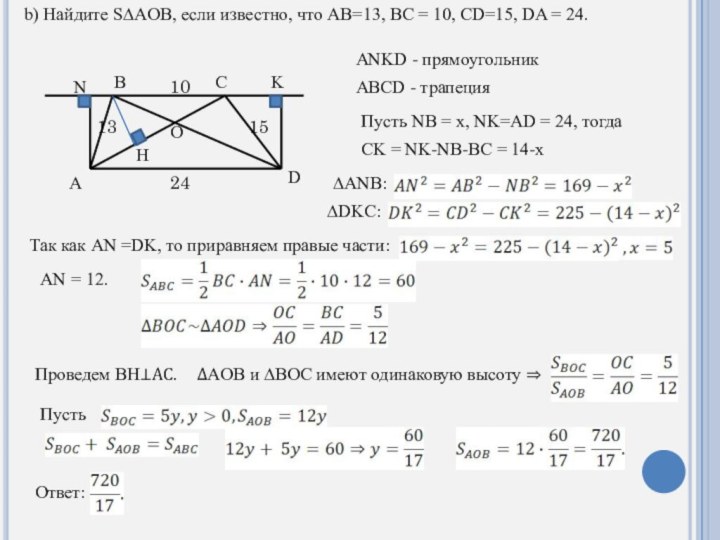
ANKD - прямоугольник
ABCD - трапеция
Пусть NB = x,
NK=AD = 24, тогда
CK = NK-NB-BC = 14-x
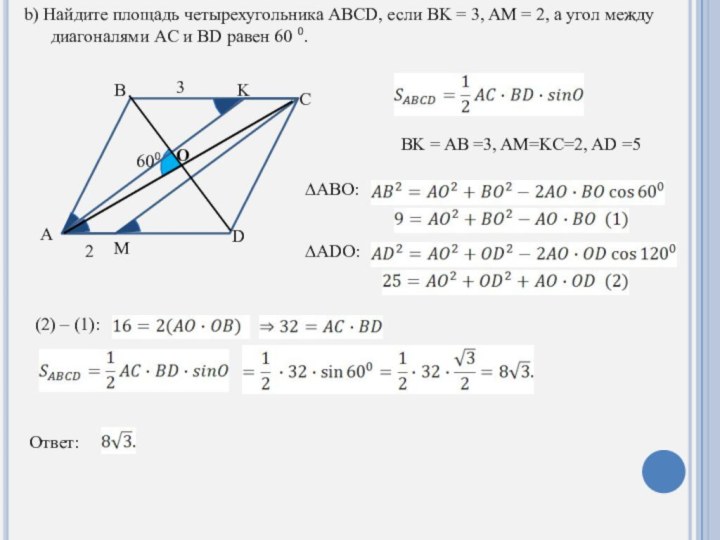
∆ANB:
∆DKC:
Так как AN =DK, то приравняем правые части:
AN = 12.
Проведем BH⊥AC. ∆AOB и ∆BOC имеют одинаковую высоту ⇒
Пусть
Ответ:
b) Найдите S∆AOB, если известно, что AB=13, BC = 10, CD=15, DA = 24.
Слайд 19
Задача №6
В четырехугольнике ABCD биссектриса угла C пересекает
сторону AD в точке M, а биссектриса угла A
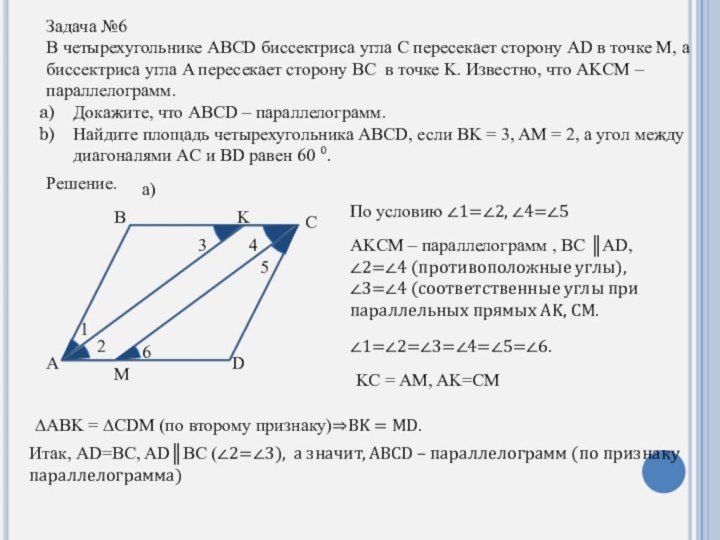
пересекает сторону BC в точке K. Известно, что AKCM – параллелограмм.Докажите, что ABCD – параллелограмм.
Найдите площадь четырехугольника ABCD, если BK = 3, AM = 2, а угол между диагоналями AC и BD равен 60 ⁰.
Решение.
1
2
3
4
5
A
C
D
M
K
B
По условию ∠1=∠2, ∠4=∠5
AKCM – параллелограмм , BC ║AD, ∠2=∠4 (противоположные углы), ∠3=∠4 (соответственные углы при параллельных прямых AK, CM.
∠1=∠2=∠3=∠4=∠5=∠6.
6
KC = AM, AK=CM
∆ABK = ∆CDM (по второму признаку)⇒BK = MD.
Итак, AD=BC, AD║BC (∠2=∠3), а значит, ABCD – параллелограмм (по признаку параллелограмма)
a)