Слайд 2
Цель
Обобщить, расширить и углубить сведения о пирамиде.
Слайд 3
Задачи:
Изучить дополнительные источники и собрать исторический и занимательный
материал о пирамиде.
Рассмотреть теоретический материал по пирамиде, выходящий за
рамки школьной программы.
Научиться применять теоремы при решении задач на пирамиду.
Изготовить развертки и модели разных пирамид.
Слайд 4
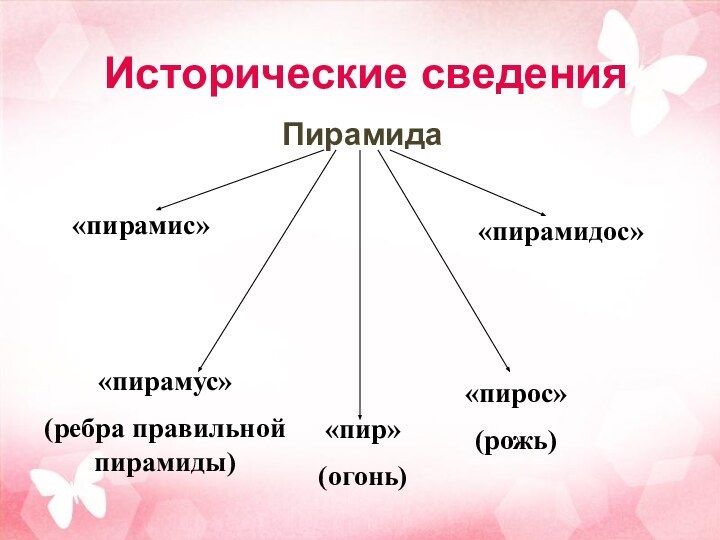
Исторические сведения
Пирамида
«пирамис»
«пирамус»
(ребра правильной пирамиды)
«пир»
(огонь)
«пирамидос»
«пирос»
(рожь)
Слайд 5
Пирамиды Фараона Хеопса XXVII в до н.э.
Крупнейшая
из египетских пирамид, единственная из «Семи чудес света», сохранившееся до наших
дней.
Слайд 6
Церковь преображения в Кижах
Слайд 8
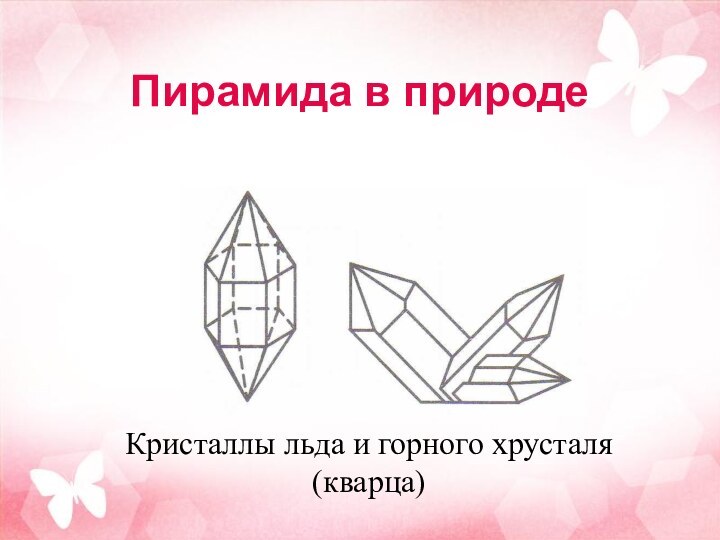
Пирамида в природе
Кристаллы льда и горного хрусталя (кварца)
Слайд 9
Картина М.Эшера, посвященная многогранникам
Слайд 10
Принцип Кавальери
Принцип:
если при пересечении двух тел плоскостями
параллельными одной и той же плоскости, в сечении всегда
получаются равновеликие между собой фигуры, то объемы этих тел равны.
Слайд 11
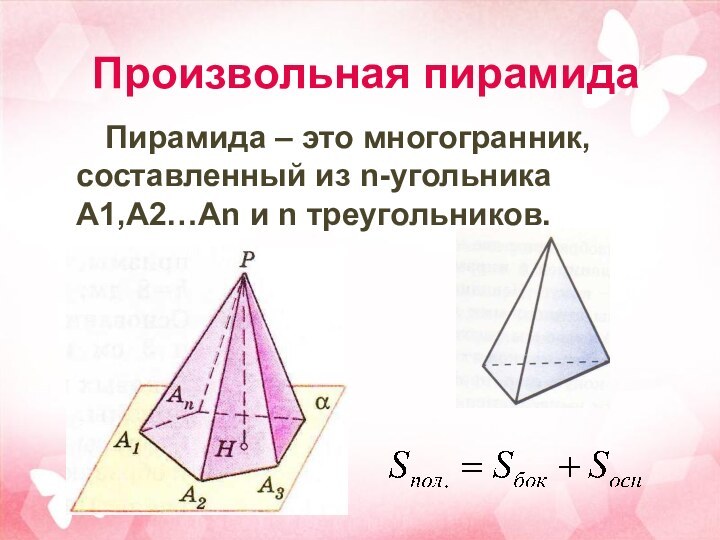
Произвольная пирамида
Пирамида – это многогранник, составленный из n-угольника
A1,A2…An и n треугольников.
Слайд 12
Заполним следующую таблицу
В-Р+Г=2
Слайд 13
Леонард Эйлер
1752 год – теорема Эйлера
Слайд 14
Сечение пирамиды
Сечением пирамиды называется многоугольник, который образуется при
пересечении пирамиды с секущей плоскостью.
Слайд 15
Утверждение
Если пирамида пересечена плоскостью, параллельной основанию, то:
Сечение –
многоугольник, подобный основанию;
Площадь сечения и основания относятся как квадраты
их расстояний от вершины.
Слайд 16
Дано: PA1A2A3 – пирамида,
|| A1A2A3
B1B2B3-сечение
S
- площадь основания
PH- высота, H1
PH
Доказать:
A1A2A3
-коэффициент подобия
S
B1B2B3
Доказательство:
SB1B2B3=
Утверждение для треугольной пирамиды
Слайд 17
Разобьем пирамиду на треугольные пирамиды с общей высотой
PH.
Поэтому площадь сечения равна.
SB1B2B3+…+SB1Bn-1Bn=
(SA1A2A3+…+SA1An-1An) =
S
Утверждение для
произвольной пирамиды
Слайд 18
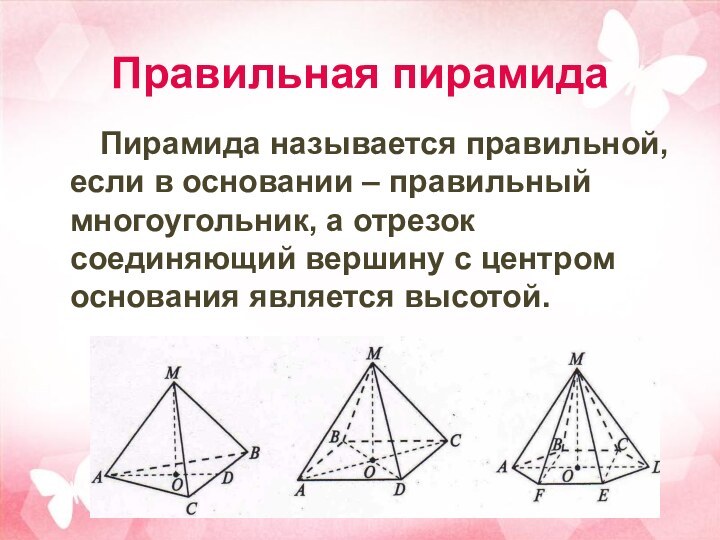
Правильная пирамида
Пирамида называется правильной, если в основании –
правильный многоугольник, а отрезок соединяющий вершину с центром основания
является высотой.
Слайд 19
Свойства правильной пирамиды
У правильной пирамиды:
боковые ребра равны;
боковые грани
являются равными равнобедренными треугольниками;
апофемы равны;
площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
Слайд 20
Дано: PA1A2…An – правильная пирамида
а – сторона основания;
h – апофема
Доказать:
1. PA1=PA2=…=PАn
2.PA1A2=PA2A3=…=PAnA1
– равнобедренные треугольники
3.PE1=PE2=…=PEn
4. Sбок.
=Pосн.h
Доказательство:
Свойства правильной пирамиды
Слайд 21
Правильный тетраэдр
Тетраэдр, гранями которого являются правильные треугольники, называется
правильным.
Слайд 22
Усеченный тетраэдр
Если срезать углы тетраэдра плоскостями, каждая из
которых отсекает третью часть его рёбер, выходящих из одной
вершины, то получим усеченный тетраэдр, имеющий восемь граней.
Слайд 23
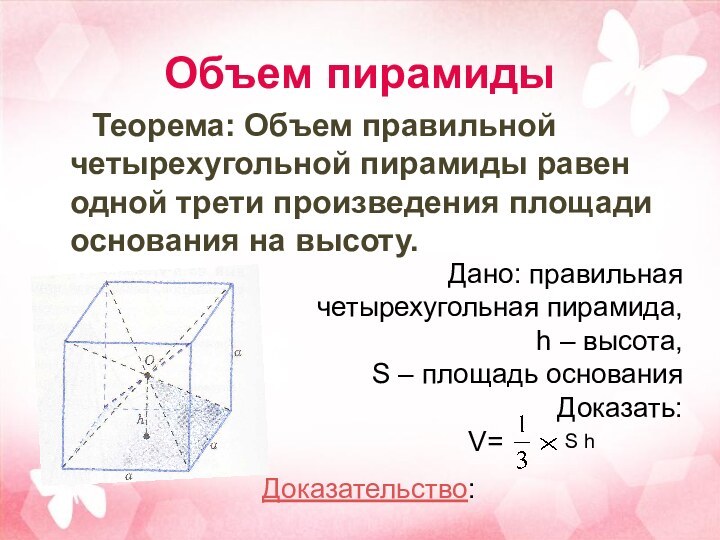
Объем пирамиды
Теорема: Объем правильной четырехугольной пирамиды равен одной
трети произведения площади основания на высоту.
Дано: правильная
четырехугольная пирамида,
h –
высота,
S – площадь основания Доказать:
V=
Доказательство:
S h
Слайд 24
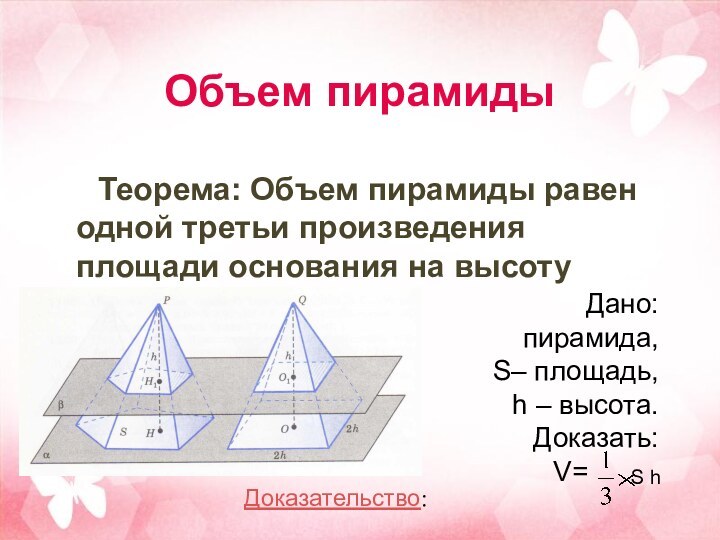
Объем пирамиды
Теорема: Объем пирамиды равен одной третьи произведения
площади основания на высоту
Дано: пирамида,
S– площадь, h –
высота.
Доказать:
V=
S h
Доказательство:
Слайд 25
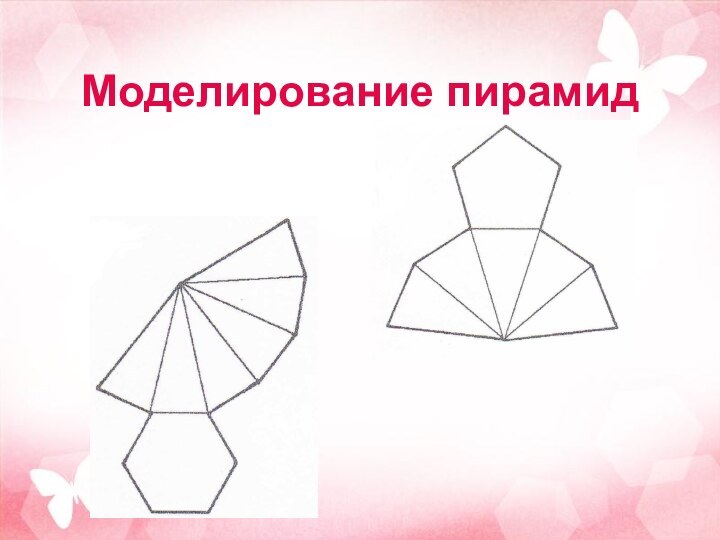
Моделирование пирамид
Если поверхность пирамиды разрезать по некоторым ребрам
и развернуть её на плоскости так, чтобы все многоугольники,
входящие в эту поверхность, лежали в данной плоскости, то полученная фигура на плоскости называется разверткой пирамиды.
Слайд 27
Задача на развертку
Можно ли квадрат «свернуть» в пирамиду,
не разрезая его? Если можно, то найдите объем пирамиды
при условии, что сторона квадрата равна а.
Слайд 28
Задача на развертку
Решение:
Объем пирамиды проще вычислить, если за
основание принять равнобедренный прямоугольный треугольник с катетами а/2. Высотой
пирамиды будет боковое ребро, равное а. Объем составит а /24 куб.ед.
Слайд 29
Задача: Найти площадь развертки правильного тетраэдра с ребром
Слайд 30
Задача: Найти площадь развертки усеченного тетраэдра с ребром
Слайд 31
Задачи
Основанием пирамиды является ромб, сторона которого равна 5
см, а одна из диагоналей равна 8 см. Найдите
боковые ребра пирамиды, если её высота проходит через точку пересечения диагоналей основания и равна 7 см.
Слайд 32
Задачи
Дано: SH=7, AB=5, DB=8.
Найти: боковые ребра.
Решение:
По теореме
Пифагора:
AH=
см;
SA=SC= см;
SB=SD= см.
Слайд 33
Задачи
Найдите объем пирамиды с высотой h, если h
= 2 м, а основанием является квадрат со стороной
3 м
Решение:
Так как V= S осн. h, а в основании лежит квадрат, то V= 3 2= 6 м
Слайд 37
Стих
О пирамидах
В Древнем Египте жил египтянин,
Был фараон он,
а может, крестьянин.
Как-то собрал он свои неликвиды,
Взял и построил
из них пирамиды.
Как бы то ни было, но отчего-то
Очень неплохо он с них заработал.
Тот египтянин теперь знаменит:
Гений финансовых он пирамид.
Слайд 38
Заключение
На изучение темы «Пирамида» в 9 классе отведен
один урок. На уроке я получила начальные сведения о
пирамиде. В данной работе я попыталась расширить свои знания. Мною был собран исторический материал о пирамиде и её объеме и занимательный материал: загадки, ребусы, кроссворды.
Слайд 39
Заключение
Так же я рассматривала теоретические вопросы, выходящие за
рамки школьного курса геометрии 9 класса. Я изготовила развертки
и модели различных пирамид, что помогает развитию пространственного воображения. При решении задач по теме «Пирамида» я повторила и обобщила знания по планиметрии. Материал, собранный в данной работе, поможет мне в дальнейшем изучении стереометрии в 10-11 классах.
Слайд 40
Литература
Геометрия, 7-9:Учебник для общеобразовательного учреждений/ Л.С. Атанасян, В.Ф.
Бутузов, С.Б. Кадомцев и др. – 14-е изд. –
М: Просвещение 2004-384с.
Геометрия, 10-11: Учебник для общеобразовательного учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 13-е изд. – М: Просвещение 2004-206с.
Зив Б.Г. Задачи к урокам геометрии 7-11 класс. – С. – Петербург, 1998 НПО «Мир и семья – 95»- 624с.
Глейзер Г.И. История математики в школе: IX – X класс Пособие для учителей. – М.: Просвещение, 1983 – 351с.
Слайд 41
Литература
Глейзер Г.И. История математики в школе: VII –
VIII класс Пособие для учителей. – М.: Просвещение, 1982
– 240с.
Игнатьев Е.И. В царстве смекалки / Под редакцией М.К. Потанова – 4-е изд. – М.: Наука 1984, 192с.
Энциклопедический словарь юного математика, - М.: Педагогика, 1985
Смирнова И.М. В мире многогранников – М.: Просвещение, 1995
Веннинджер М. Модели Многогранников – М.Мир, 1974
Штейнгауз Г. Математический калейдоскоп
Штейнгауз Г. Сто задач. – М: Наука, 1982