- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Правильные многогранники (10 класс)
Содержание
- 2. С глубокой древности человеку известны пять удивительных многогранников
- 3. По числу граней их называют правильный тетраэдр (четырёхгранник)
- 4. гексаэдр (шестигранник) или куб
- 5. октаэдр (восьмигранник)
- 6. додекаэдр (двенадцатигранник)
- 7. икосаэдр (двадцатигранник)
- 8. Свойства этих многогранников изучали ученые и священники,
- 9. Великий древнегреческий философ Платон, живший в IV
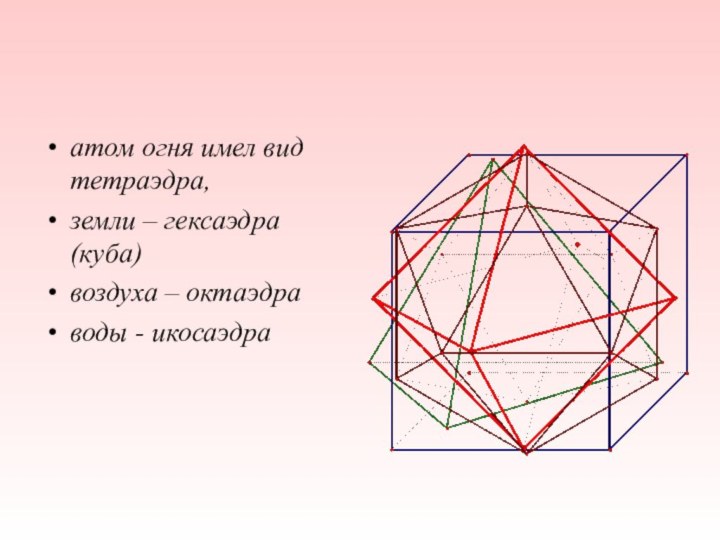
- 10. Четыре сущности природы были известны человечеству: огонь,
- 11. атом огня имел вид тетраэдра,земли – гексаэдра (куба)воздуха – октаэдраводы - икосаэдра
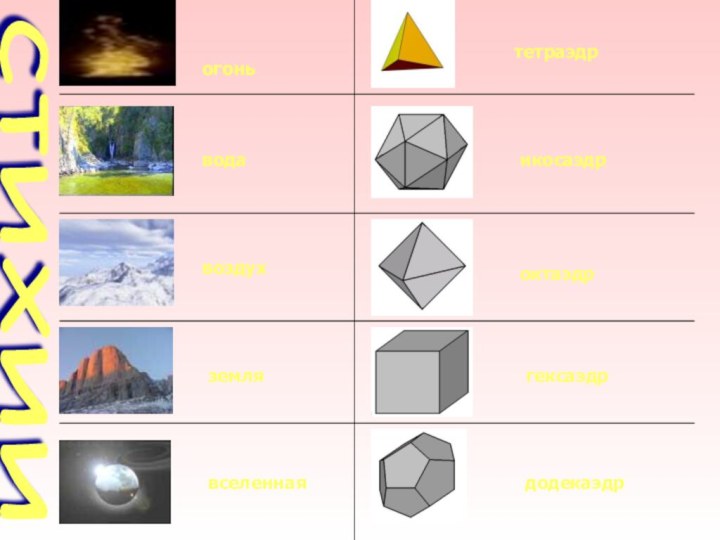
- 12. огонь тетраэдрвода икосаэдр воздух октаэдр земля гексаэдр вселенная додекаэдр стихии
- 13. Платон и его ученики в своих работах
- 14. Определение правильного многогранникаМногогранник называется правильным, если все
- 15. Платоновы тела - трехмерный аналог плоских правильных
- 16. Доказательство этого факта известно уже более двух
- 17. Существует лишь пять выпуклых правильных многогранников -
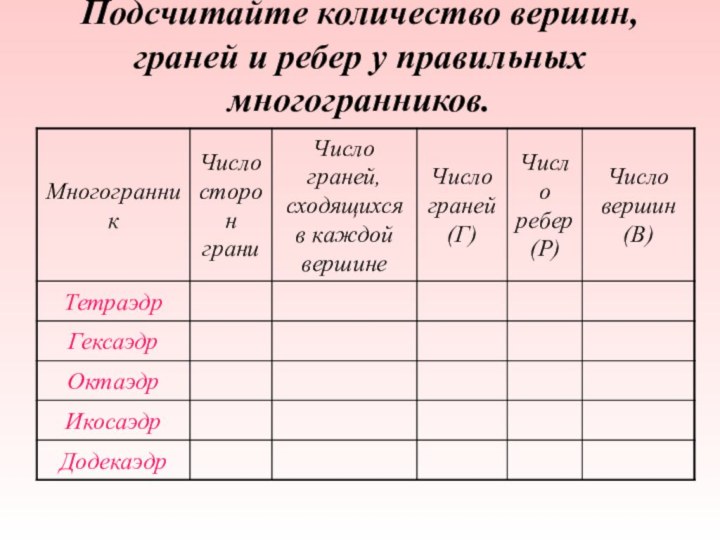
- 18. Подсчитайте количество вершин, граней и ребер у правильных многогранников.
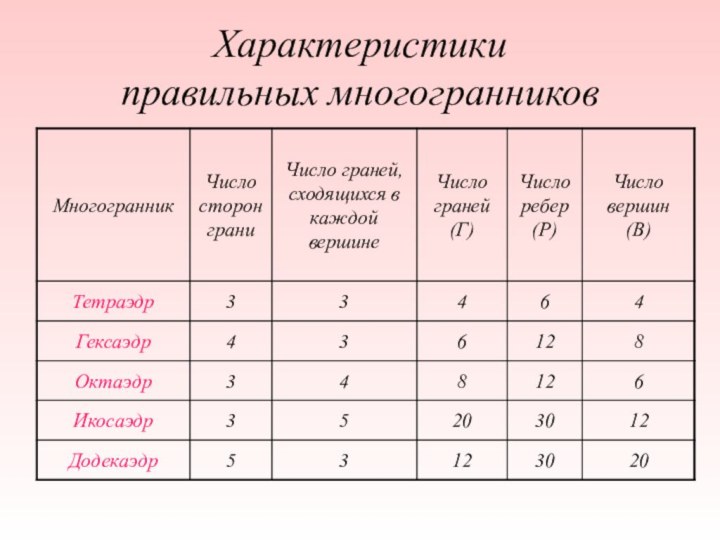
- 19. Характеристики правильных многогранников
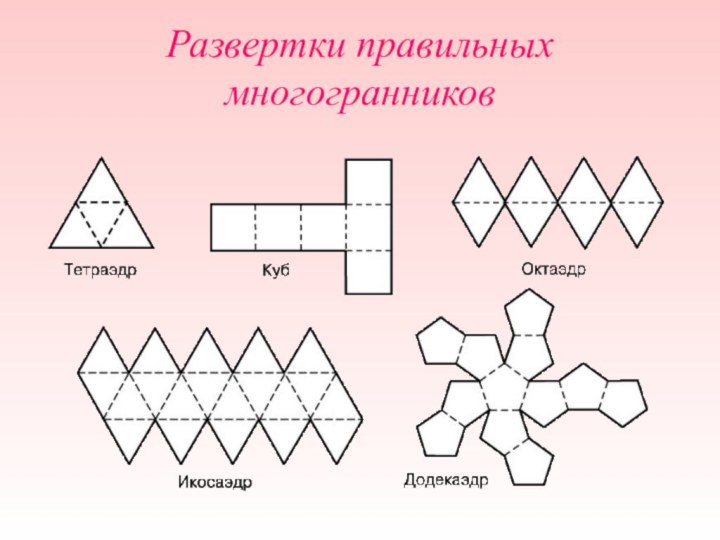
- 20. Развертки правильных многогранников
- 21. Двойственность правильных многогранниковГексаэдр (куб) и октаэдр образуют
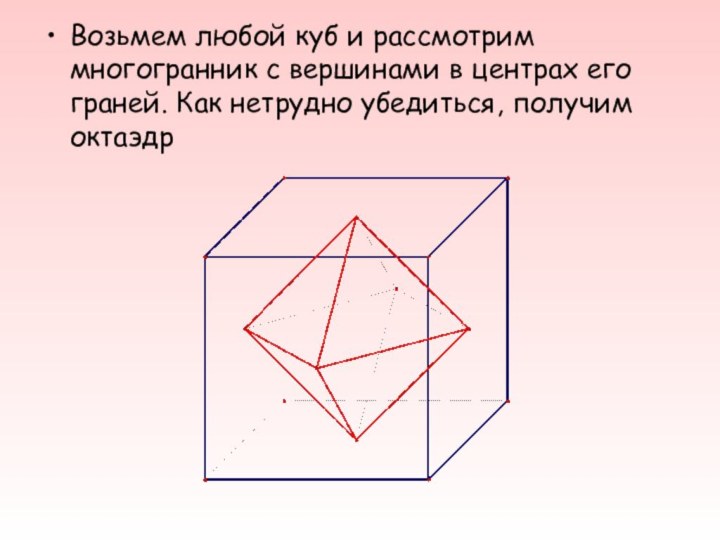
- 22. Возьмем любой куб и рассмотрим многогранник с
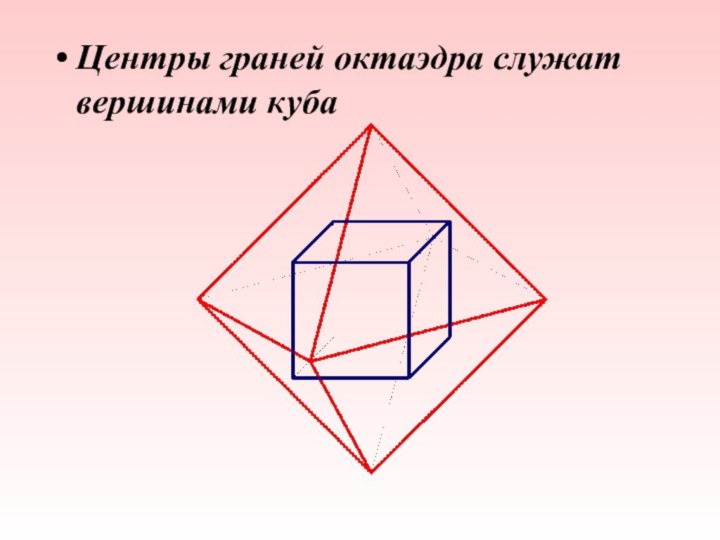
- 23. Центры граней октаэдра служат вершинами куба
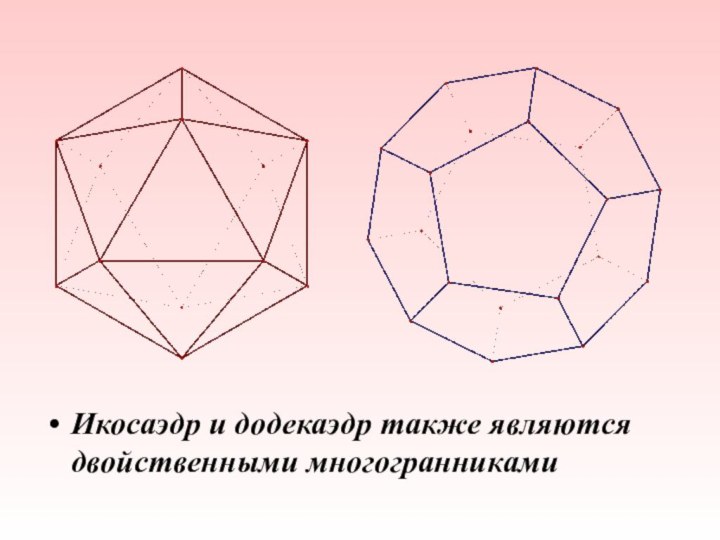
- 24. Икосаэдр и додекаэдр также являются двойственными многогранниками
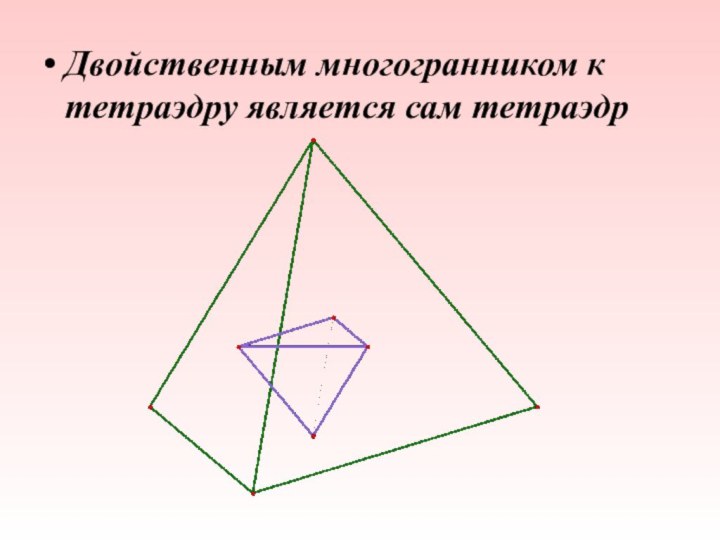
- 25. Двойственным многогранником к тетраэдру является сам тетраэдр
- 26. Тестирование.
- 27. 1. Поверхность, составленная из четырех треугольниковА) ТЕТРАЭДРС) КВАДРАТB) ПАРАЛЛЕЛЕПИПЕДD) ШАР
- 28. 2. Поверхность, составленная из многоугольников и ограничива- ющая некоторое геометрическое телоА) МНОГОУГОЛЬНИКС) ТРЕУГОЛЬНИКB) МНОГОГРАННИКD) КВАДРАТ
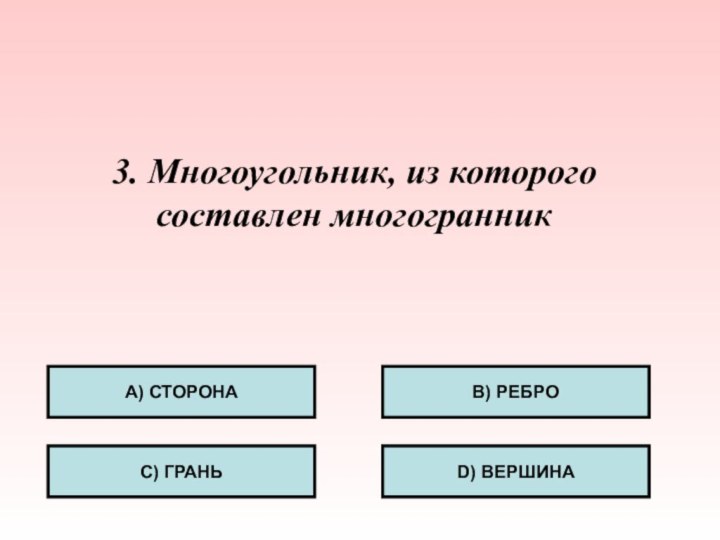
- 29. 3. Многоугольник, из которого составлен многогранникА) СТОРОНАС) ГРАНЬB) РЕБРОD) ВЕРШИНА
- 30. 4. Отрезок, соединяющий две вершины, не принадлежащие одной граниА) ДИАГОНАЛЬС) ВЫСОТАB) МЕДИАНАD) АПОФЕМА
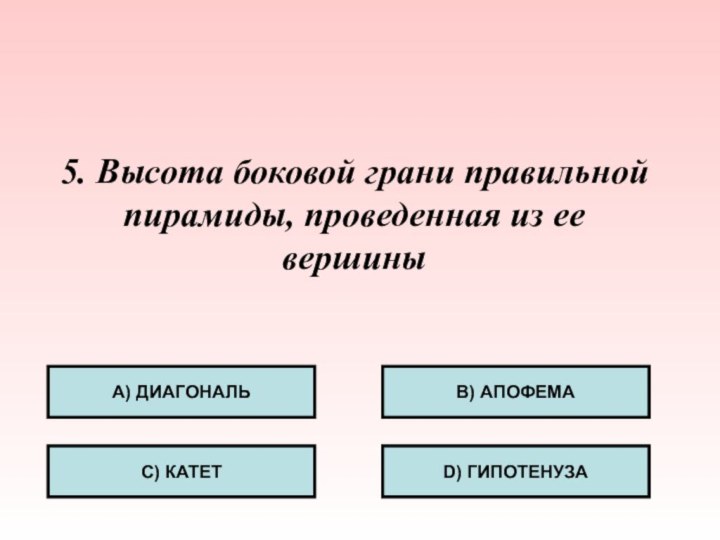
- 31. 5. Высота боковой грани правильной пирамиды, проведенная из ее вершины А) ДИАГОНАЛЬС) КАТЕТB) АПОФЕМАD) ГИПОТЕНУЗА
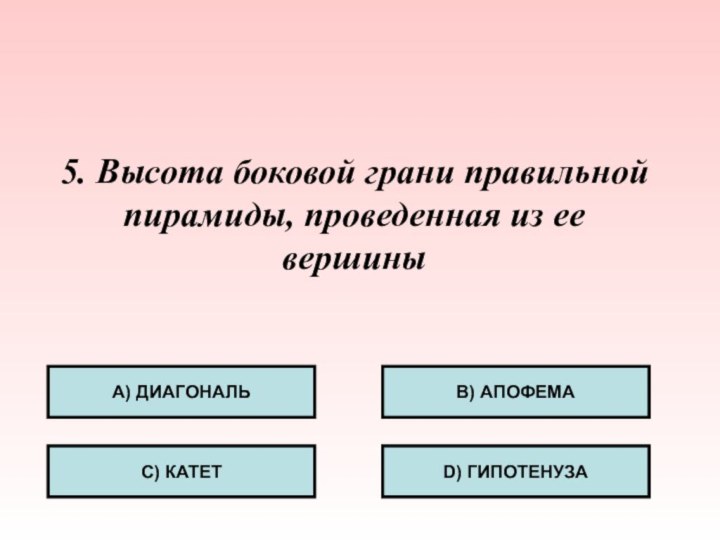
- 32. 5. Высота боковой грани правильной пирамиды, проведенная из ее вершины А) ДИАГОНАЛЬС) КАТЕТB) АПОФЕМАD) ГИПОТЕНУЗА
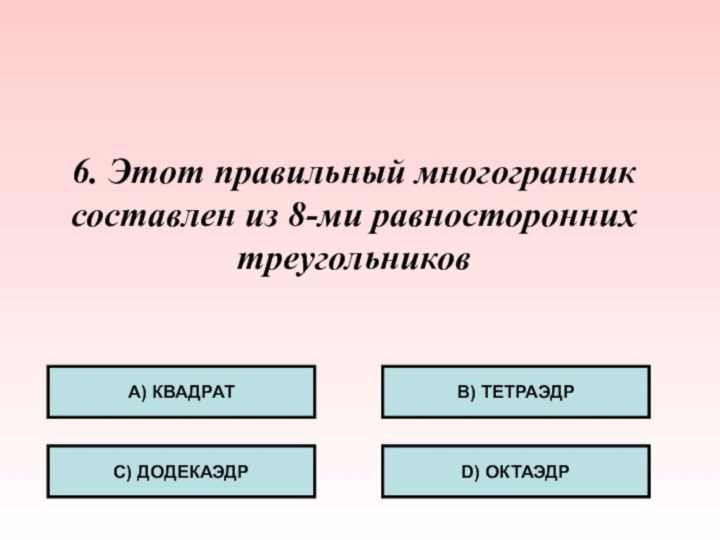
- 33. 6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников А) КВАДРАТС) ДОДЕКАЭДРB) ТЕТРАЭДРD) ОКТАЭДР
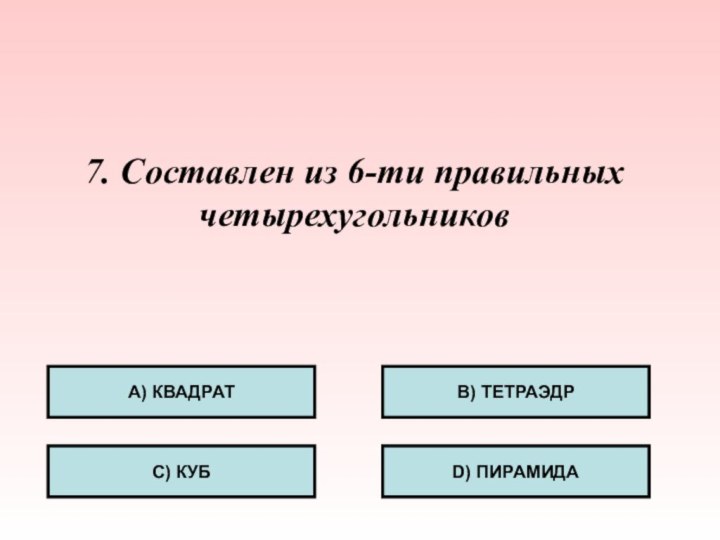
- 34. 7. Составлен из 6-ти правильных четырехугольников А) КВАДРАТС) КУБB) ТЕТРАЭДРD) ПИРАМИДА
- 35. 8. Стихия тетраэдра А) ВОДАС) ЗЕМЛЯB) ВОЗДУХD) ОГОНЬ
- 36. 9. Многоугольник, подобный пчелиным сотамА) 8-МИ УГОЛЬНИКС) 4-Х УГОЛЬНИКB) 6-ТИ УГОЛЬНИКD) ТРЕУГОЛЬНИК
- 37. Проверь себя.1. A2. B3. C4. A5. B6. D7. C8. D9. B
- 38. По горизонтали: 1. Количество сходящихся ребер у
- 39. Скачать презентацию
- 40. Похожие презентации
С глубокой древности человеку известны пять удивительных многогранников





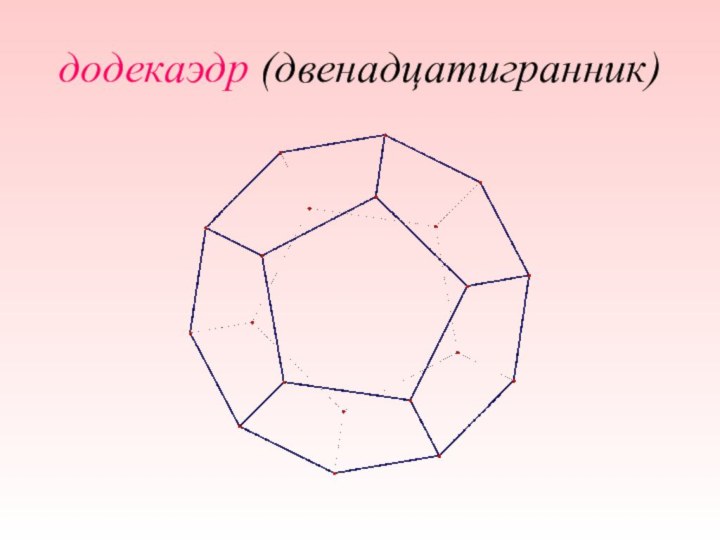















Слайд 8 Свойства этих многогранников изучали ученые и священники, их
модели можно было увидеть в работах архитекторов и ювелиров,
им приписывались различные магические и целебные свойстваСлайд 9 Великий древнегреческий философ Платон, живший в IV –
V вв. до нашей эры, считал, что эти тела
олицетворяют сущность природыСлайд 10 Четыре сущности природы были известны человечеству: огонь, вода,
земля и воздух. По мнению Платона, их атомы имели
вид правильных многогранниковСлайд 13 Платон и его ученики в своих работах большое
внимание уделяли перечисленным многогранникам. Поэтому эти многогранники называют также
платоновыми телами
Слайд 14
Определение правильного многогранника
Многогранник называется правильным, если все его
грани – равные между собой правильные многоугольники, из каждой
вершины выходит одинаковое число ребер и все двугранные углы равныСлайд 15 Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Однако между двумерным и трехмерным случаями есть важное отличие:
существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранниковСлайд 16 Доказательство этого факта известно уже более двух тысяч
лет; этим доказательством и изучением пяти правильных тел завершаются
"Начала" ЕвклидаСлайд 17 Существует лишь пять выпуклых правильных многогранников - тетраэдр,
октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с
квадратными гранями и додекаэдр с пятиугольными гранями
Слайд 21
Двойственность правильных многогранников
Гексаэдр (куб) и октаэдр образуют двойственную
пару многогранников. Число граней одного многогранника равно числу вершин
другого и наоборот.Слайд 22 Возьмем любой куб и рассмотрим многогранник с вершинами
в центрах его граней. Как нетрудно убедиться, получим октаэдр
Слайд 27
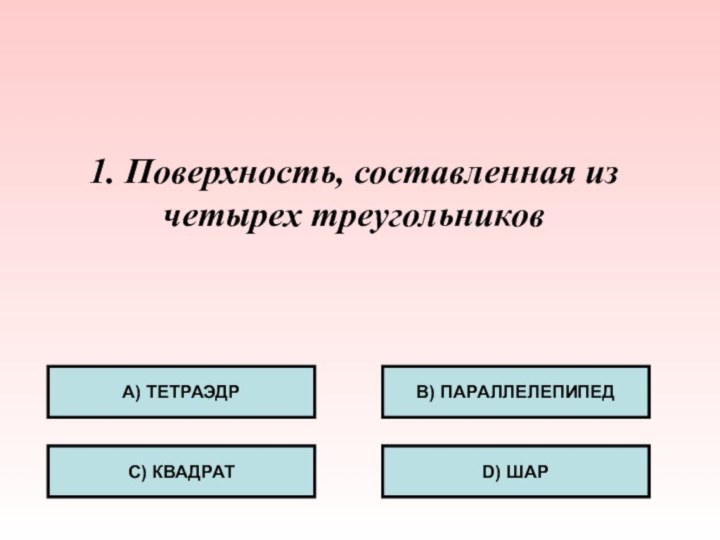
1. Поверхность, составленная из четырех треугольников
А) ТЕТРАЭДР
С) КВАДРАТ
B)
ПАРАЛЛЕЛЕПИПЕД
D) ШАР
Слайд 28 2. Поверхность, составленная из многоугольников и ограничива- ющая
некоторое геометрическое тело
А) МНОГОУГОЛЬНИК
С) ТРЕУГОЛЬНИК
B) МНОГОГРАННИК
D) КВАДРАТ
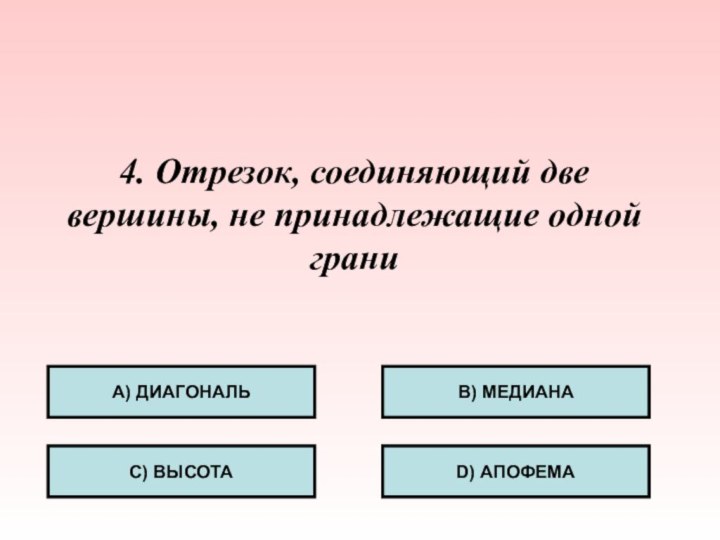
Слайд 30 4. Отрезок, соединяющий две вершины, не принадлежащие одной
грани
А) ДИАГОНАЛЬ
С) ВЫСОТА
B) МЕДИАНА
D) АПОФЕМА
Слайд 31 5. Высота боковой грани правильной пирамиды, проведенная из
ее вершины
А) ДИАГОНАЛЬ
С) КАТЕТ
B) АПОФЕМА
D) ГИПОТЕНУЗА
Слайд 32 5. Высота боковой грани правильной пирамиды, проведенная из
ее вершины
А) ДИАГОНАЛЬ
С) КАТЕТ
B) АПОФЕМА
D) ГИПОТЕНУЗА
Слайд 33 6. Этот правильный многогранник составлен из 8-ми равносторонних
треугольников
А) КВАДРАТ
С) ДОДЕКАЭДР
B) ТЕТРАЭДР
D) ОКТАЭДР
Слайд 36
9. Многоугольник, подобный пчелиным сотам
А) 8-МИ УГОЛЬНИК
С) 4-Х
УГОЛЬНИК
B) 6-ТИ УГОЛЬНИК
D) ТРЕУГОЛЬНИК
Слайд 38
По горизонтали:
1. Количество сходящихся ребер у октаэдра. 2.
Грань додекаэдра.
3. Боковая грань усеченной пирамиды.
4. Правильный
многогранник. По вертикали: 2. Граница многогранника.
5. Правильная треугольная пирамида.
6. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
1
2
2
3
4
6
5
ч
е
т
ы
р
е
п
я
т
и
у
г
о
л
ь
н
и
к
т
р
а
п
е
ц
и
я
о
о
к
т
а
э
д
р
о
в
е
х
н
с
т
ь
т
т
р
э
д
р
в
с
т
а
Кроссворд