Презентация на тему Определение и признак перпендикулярности плоскостей

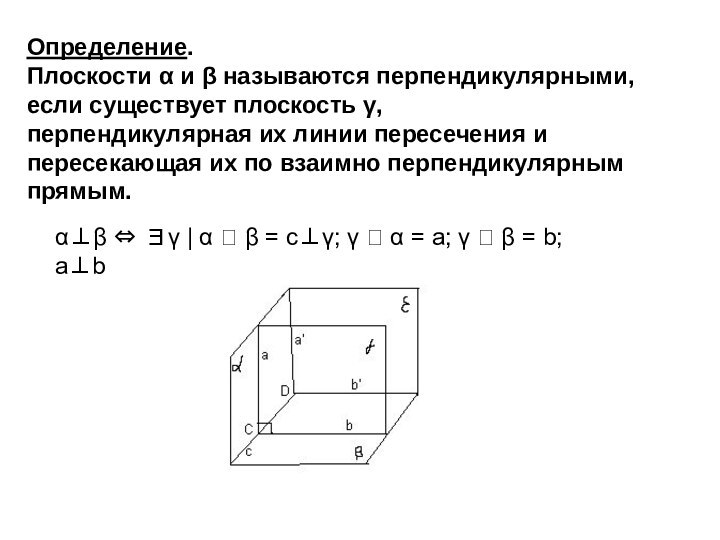
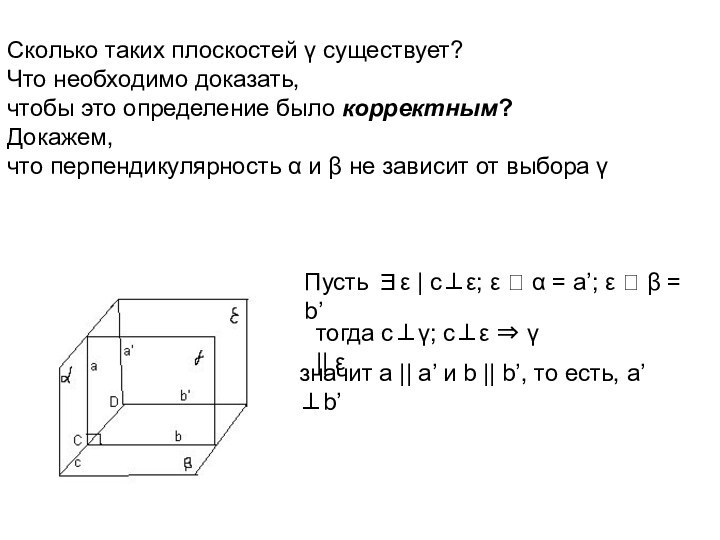
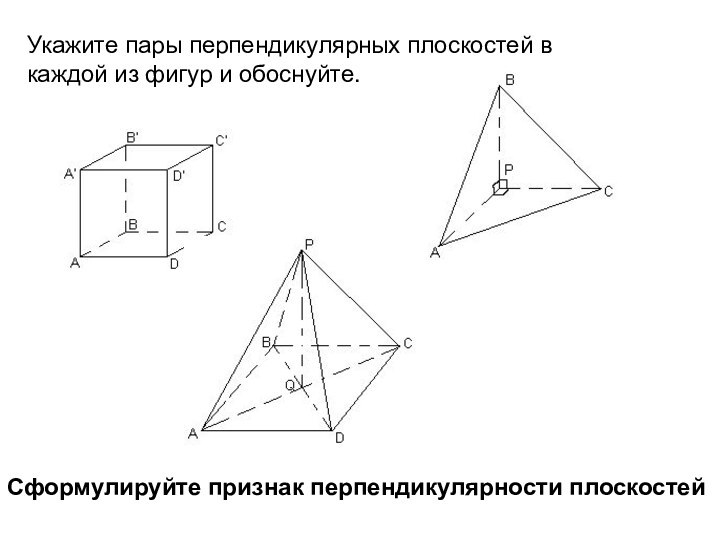
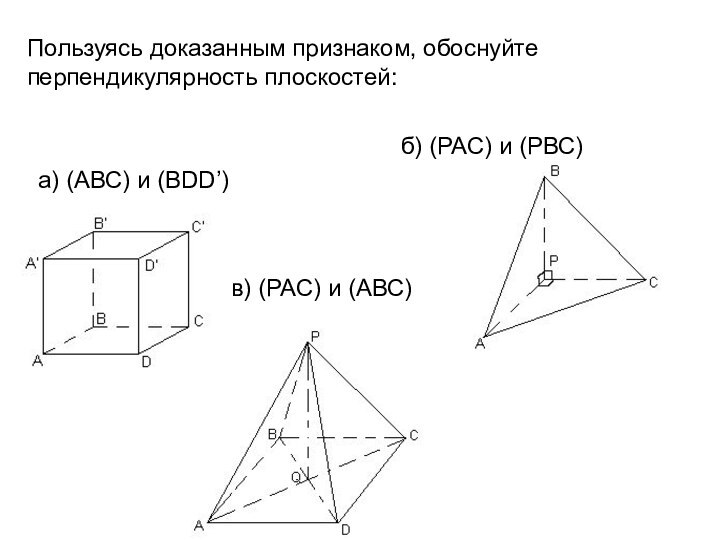
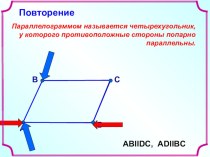
параллельную данной прямой
и проходящую через
а) заданную точку;
б)

Пусть а || b, а || α, b имеет с плоскостью α общую точку.
Докажите, что прямая b лежит в плоскости α

существует плоскость γ,
перпендикулярная их линии пересечения и
пересекающая

α⊥β ⇔ ∃γ | α  β = c⊥γ; γ  α = a; γ  β = b; a⊥b

чтобы это определение было корректным?
Докажем,
что перпендикулярность α

Пусть ∃ε | c⊥ε; ε  α = a’; ε  β = b’

тогда c⊥γ; c⊥ε ⇒ γ || ε

значит a || a’ и b || b’, то есть, a’⊥b’

и обоснуйте.
Сформулируйте признак перпендикулярности плоскостей

то эти плоскости перпендикулярны
Доказательство.
Пусть а  β =

Дано: а⊥β; а⊂α. Доказать: α⊥β.