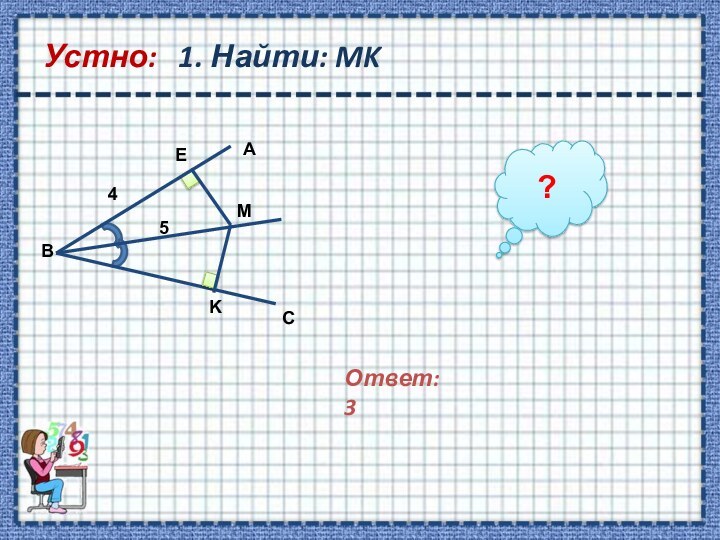
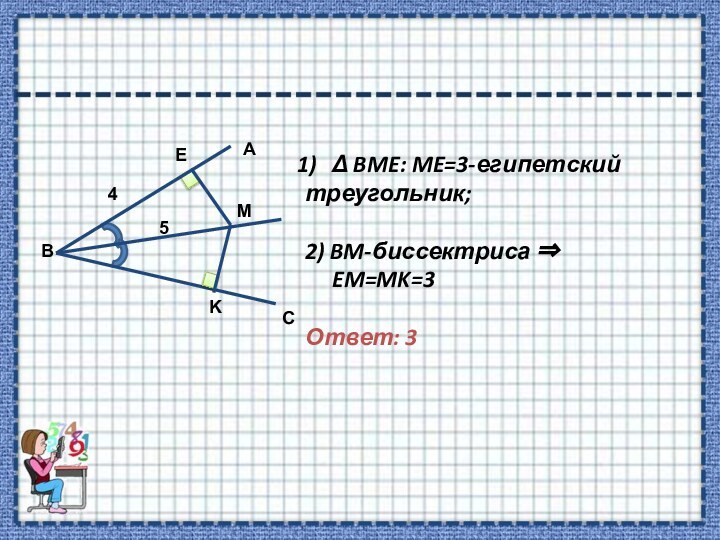
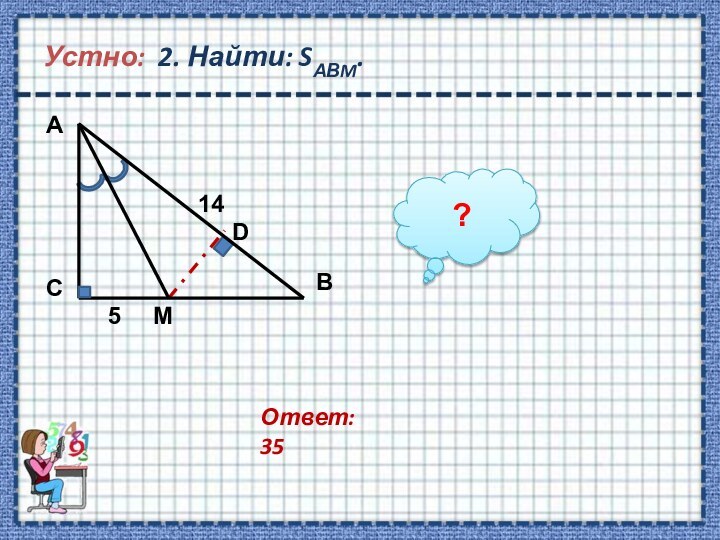
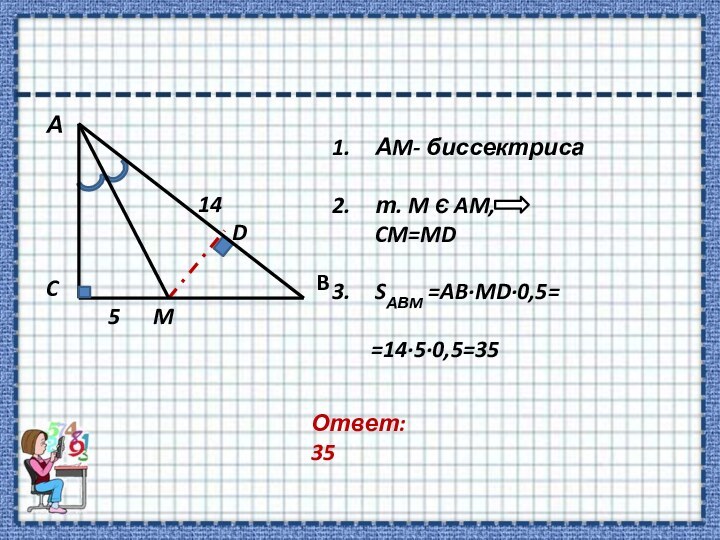
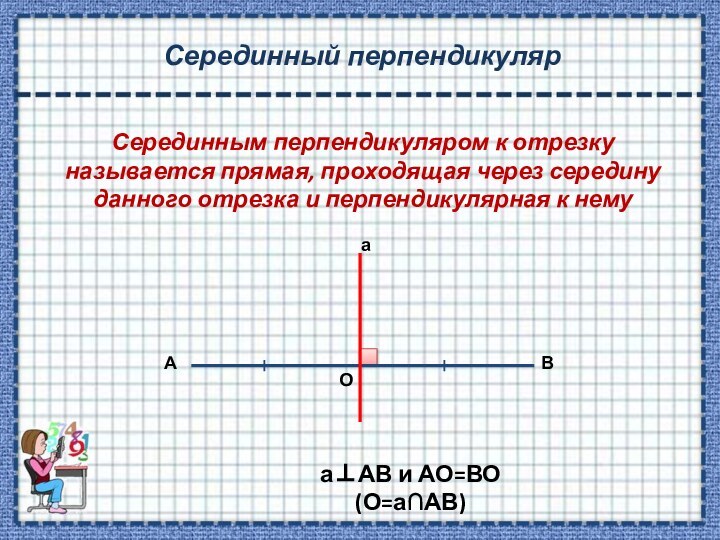
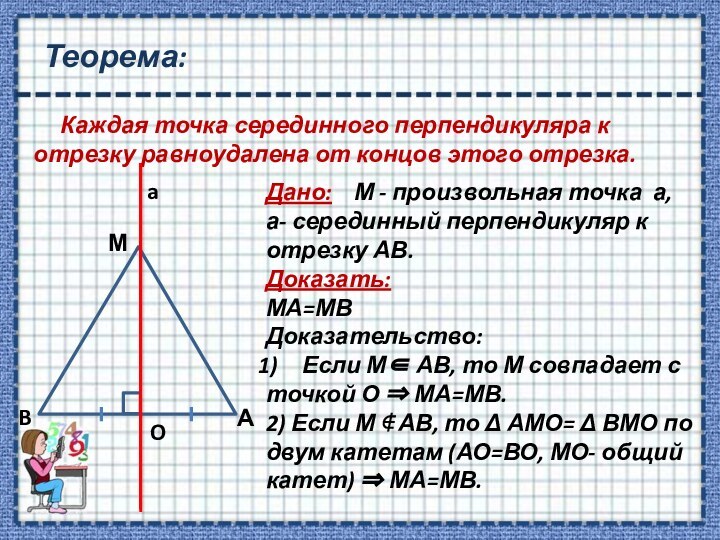
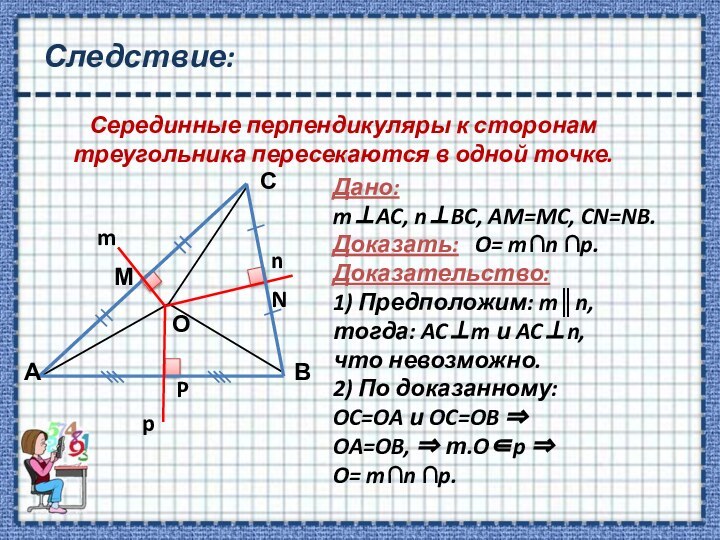
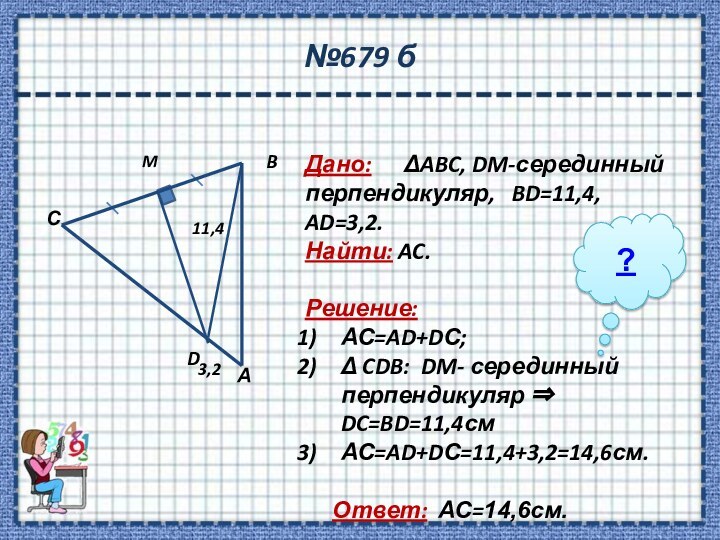
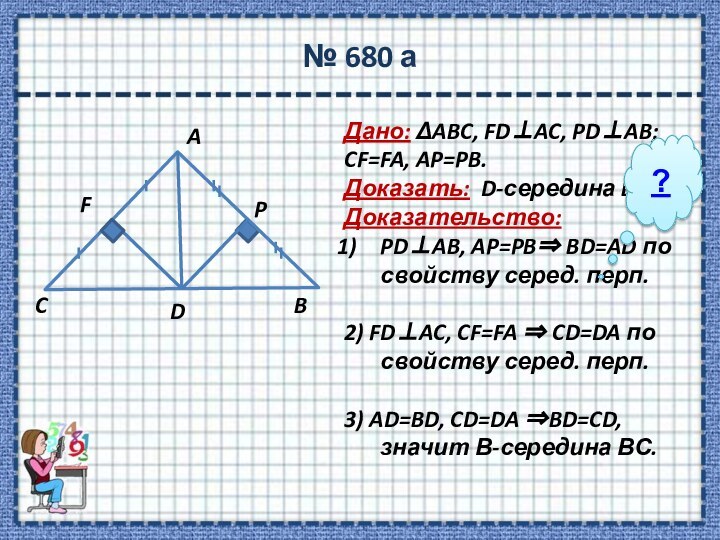
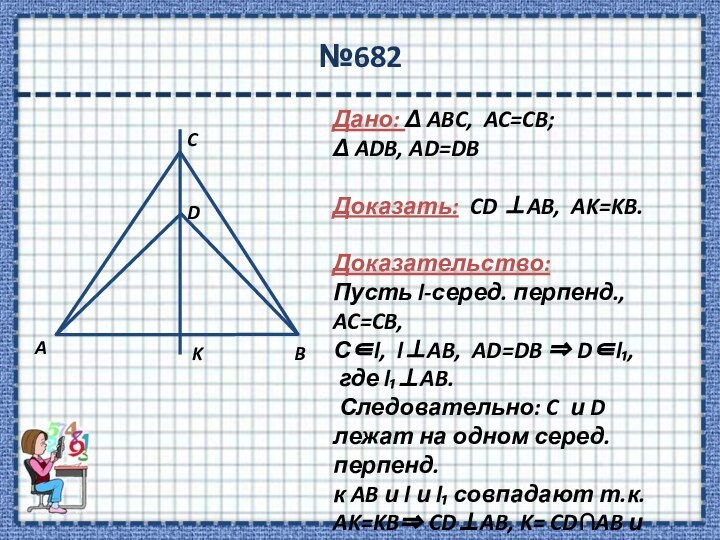
перпендикуляре
Цели:
ввести понятие серединного перпендикуляра к отрезку;
рассмотреть теорему о
серединном перпендикуляре и следствие из него;Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.