- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основные фигуры в пространстве
Содержание
- 2. ТочкаAПрописные латинские буквы A, B, C, D, E, K, …
- 3. ПрямаяaСтрочные латинские буквы a, b, c, d, e, k, …
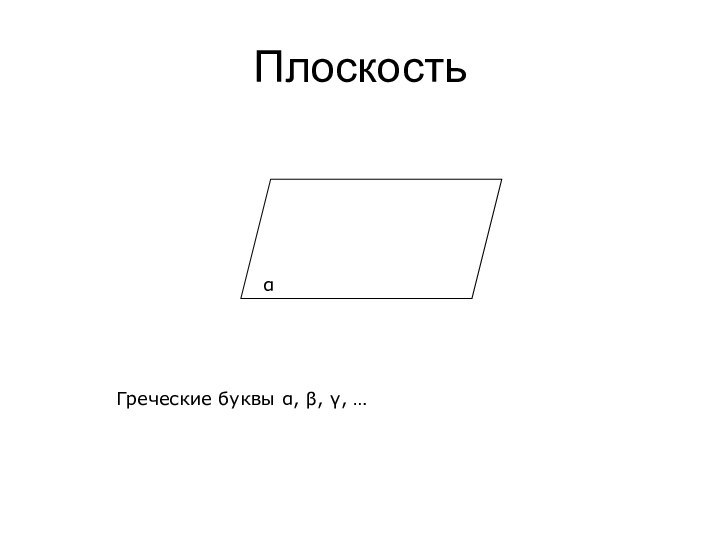
- 4. ПлоскостьαГреческие буквы α, β, γ, …
- 5. Взаимное расположение точек, прямых, плоскостей в пространстве.
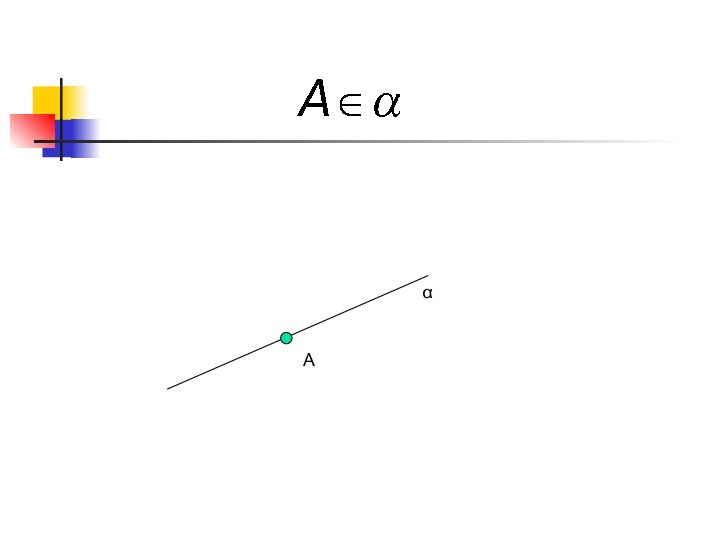
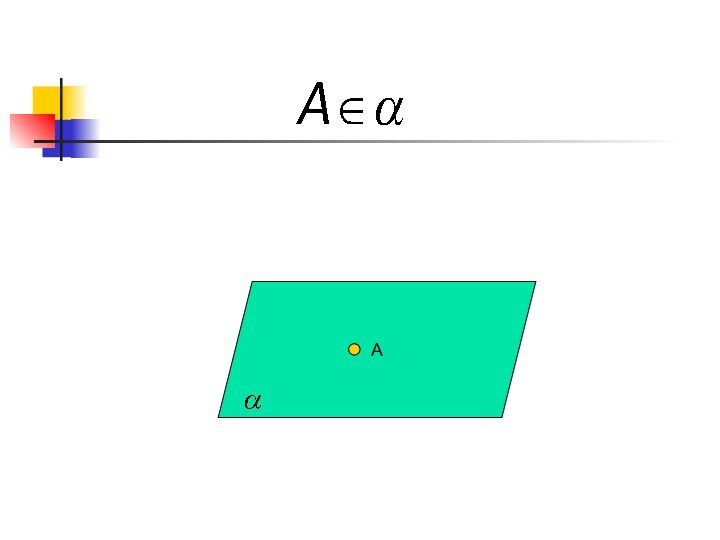
- 6. Aα
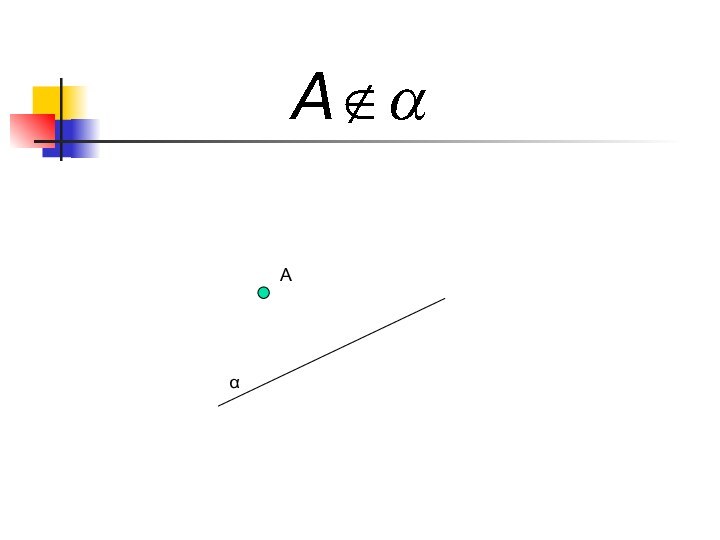
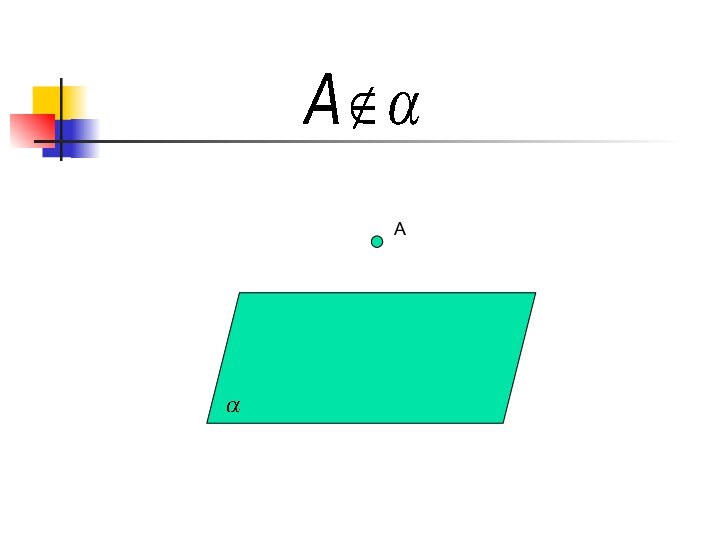
- 7. αA
- 8. A
- 9. A
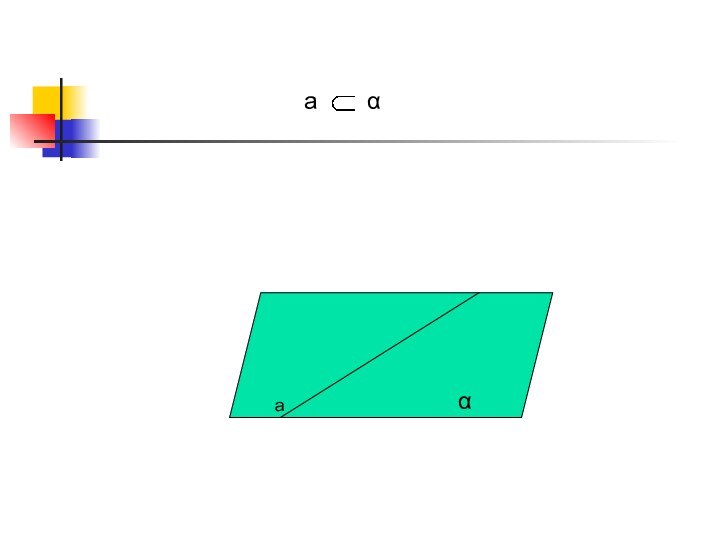
- 10. aαaα
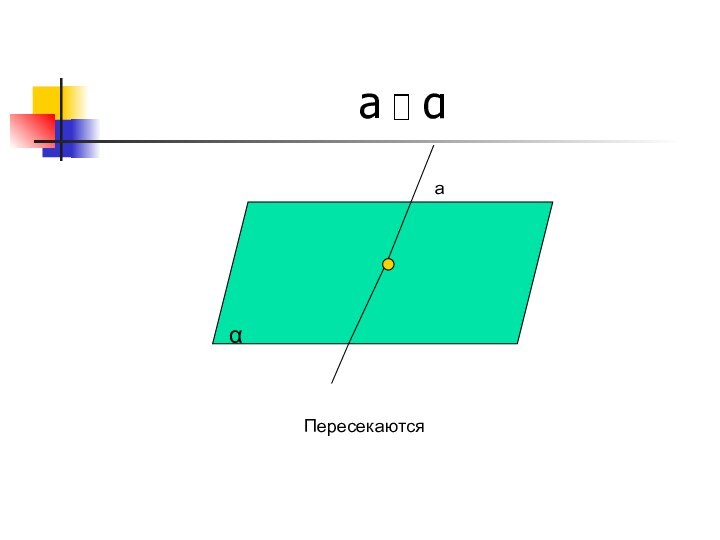
- 11. a αaПересекаютсяα
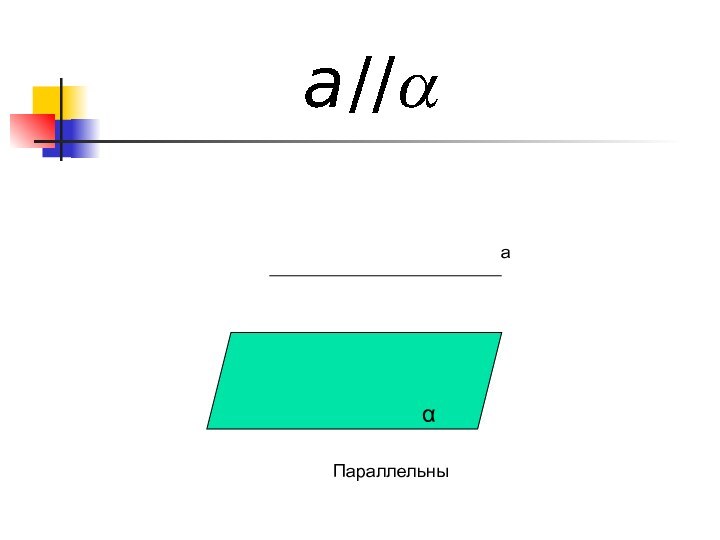
- 12. aПараллельныα
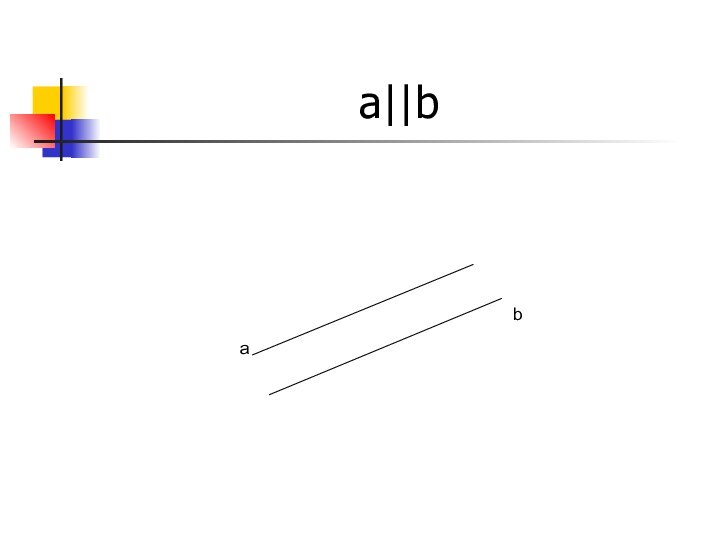
- 13. a||bab
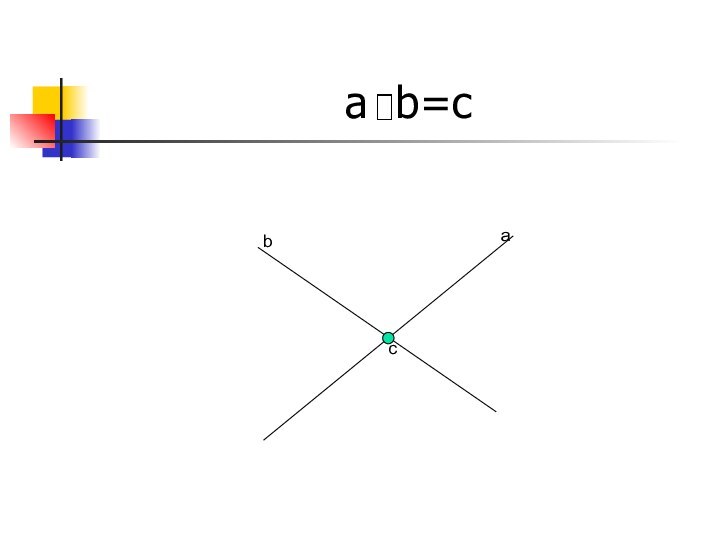
- 14. a b=cabc
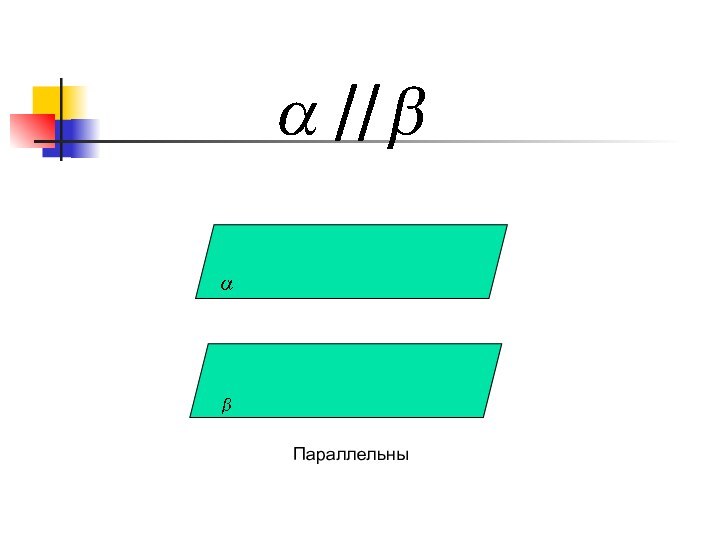
- 15. Параллельны
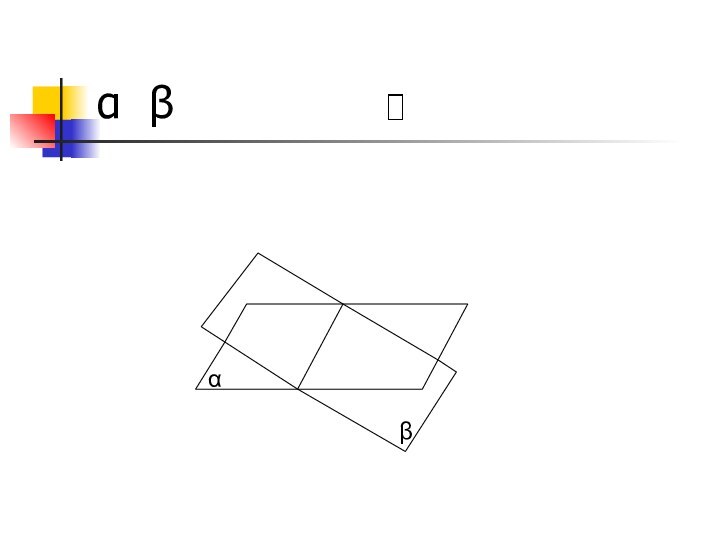
- 16. α β αβ
- 17. Аксиомы стереометрии
- 18. ABCαЧерез любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
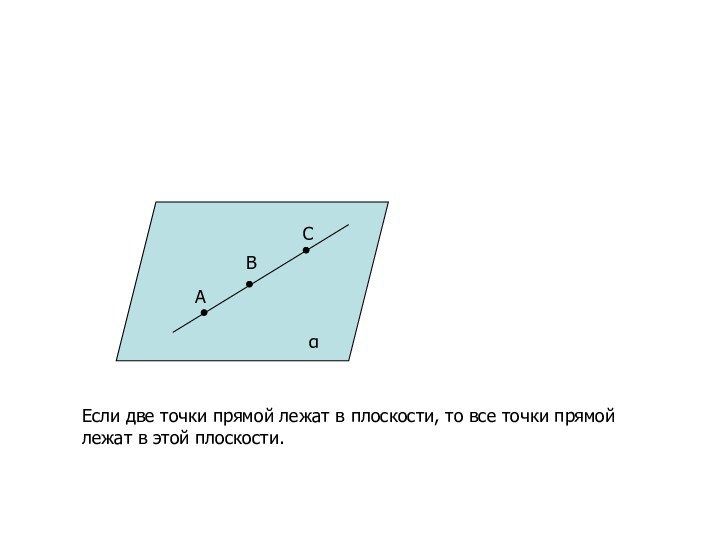
- 19. ABCαЕсли две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
- 21. Следствия из аксиом стереометрии. Теорема 1.Через прямую
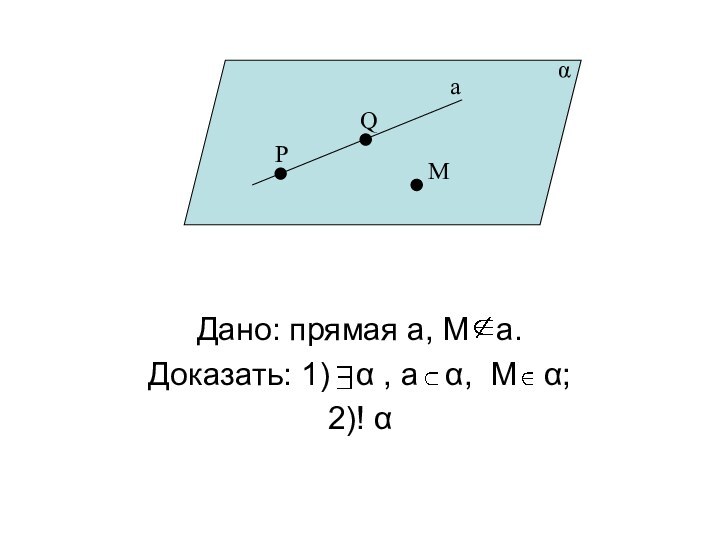
- 22. Дано: прямая а, М a.Доказать: 1)
- 23. Доказательство.Возьмем точки Р a, Q
- 24. Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
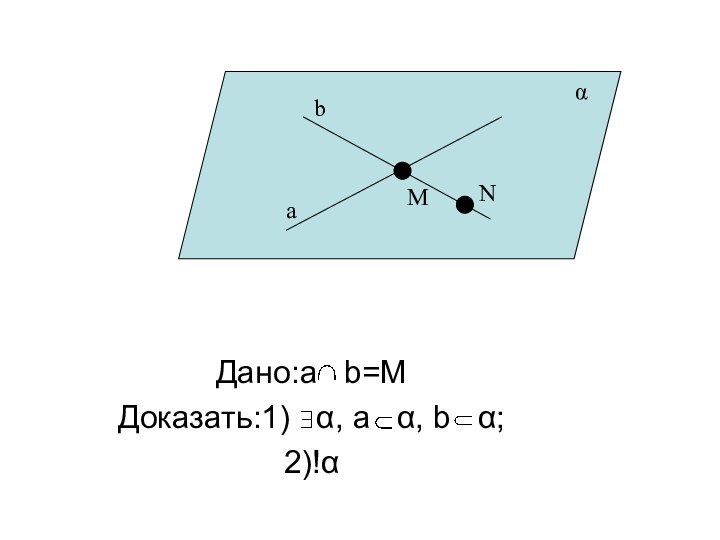
- 25. Дано:a b=MДоказать:1) α, а α, b α;2)!αabMNα
- 26. ДоказательствоВозьмем точку N b. По Т1 α,
- 27. Способы задания плоскости в пространстве
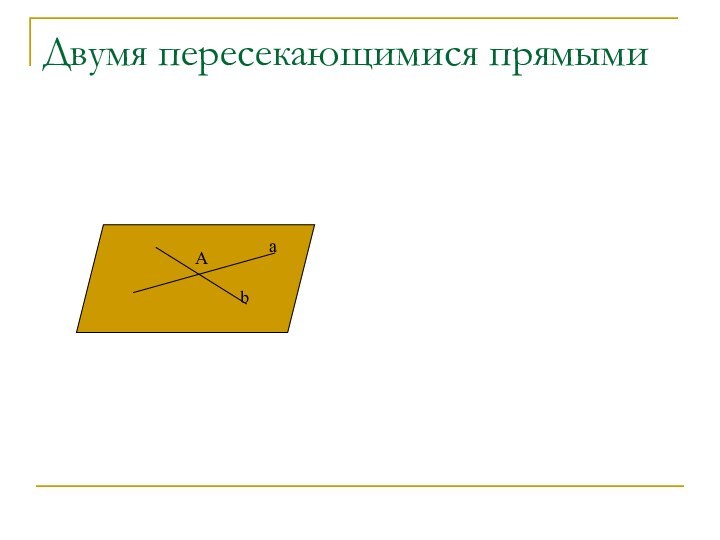
- 28. Двумя пересекающимися прямымиAab
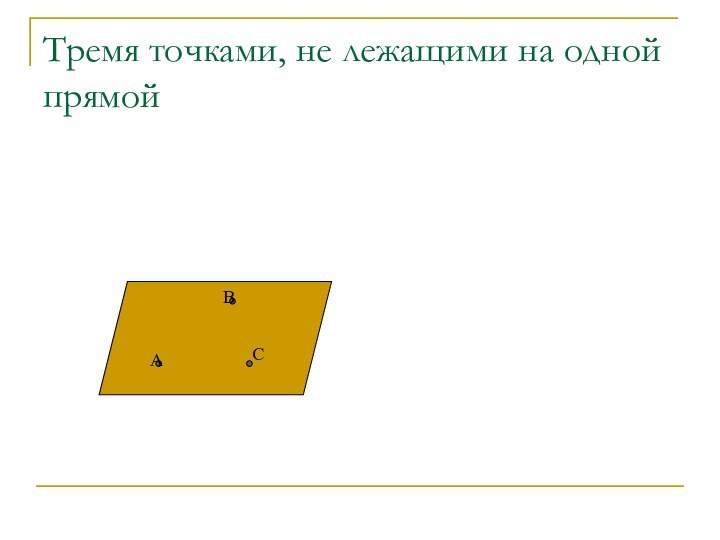
- 29. Тремя точками, не лежащими на одной прямойABC
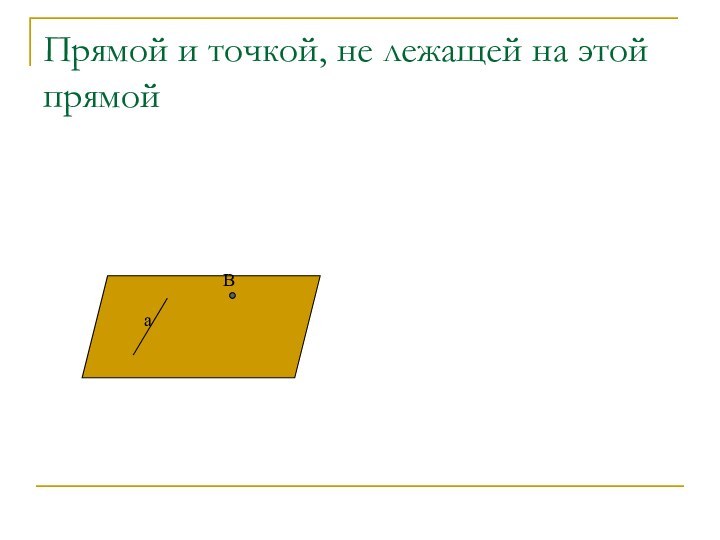
- 30. Прямой и точкой, не лежащей на этой прямойBa
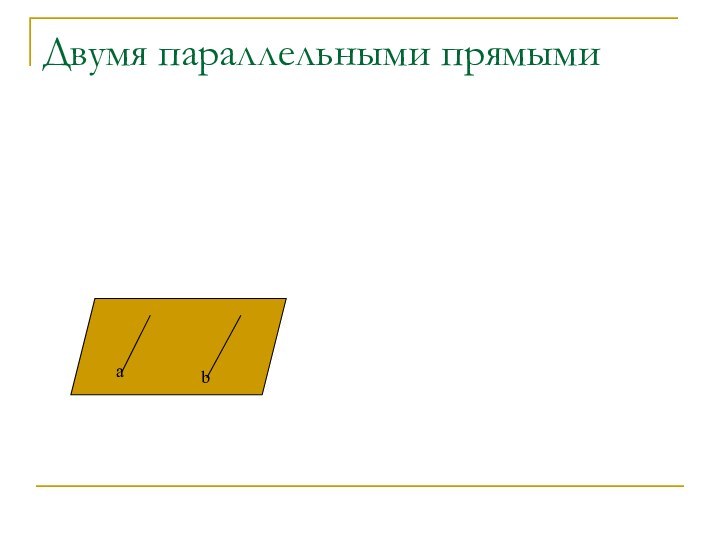
- 31. Двумя параллельными прямымиab
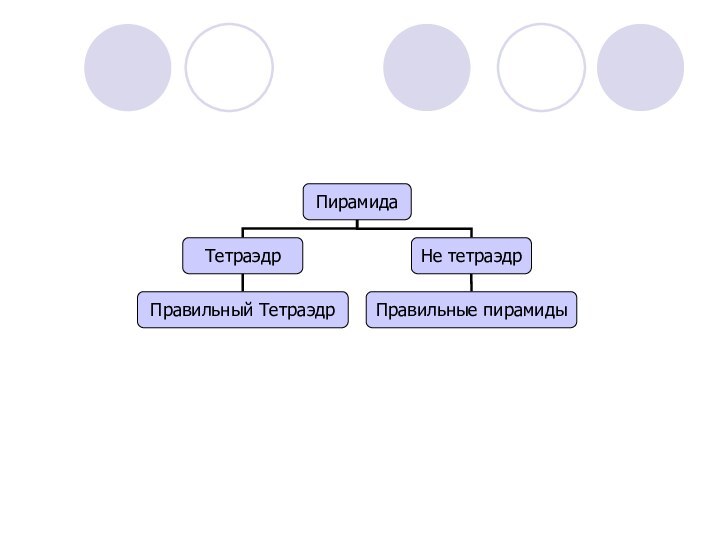
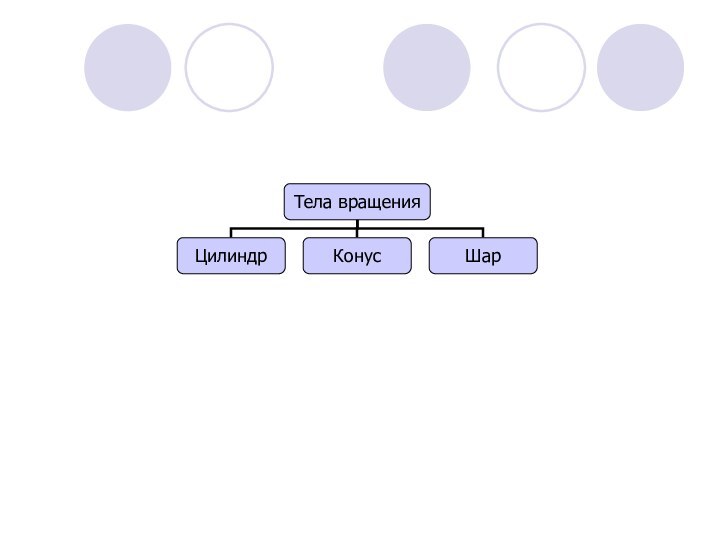
- 32. Многогранники. Тела вращения.
- 36. Скачать презентацию
- 37. Похожие презентации
ТочкаAПрописные латинские буквы A, B, C, D, E, K, …













Слайд 18
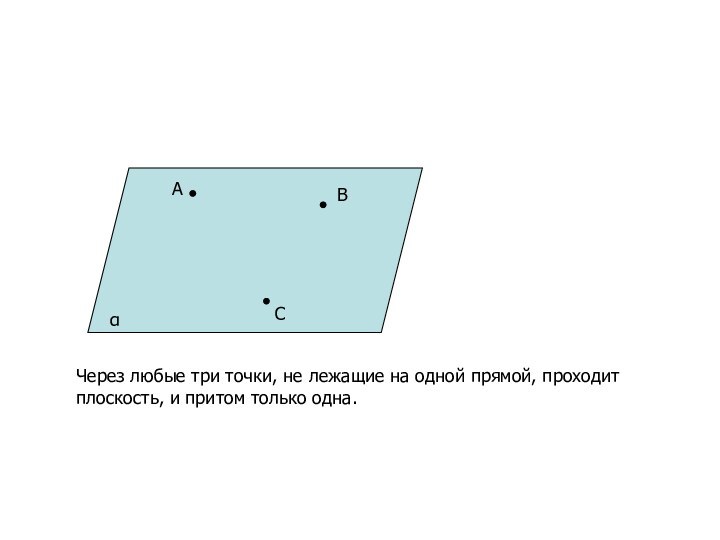
A
B
C
α
Через любые три точки, не лежащие на одной
прямой, проходит
плоскость, и притом только одна.
Слайд 20
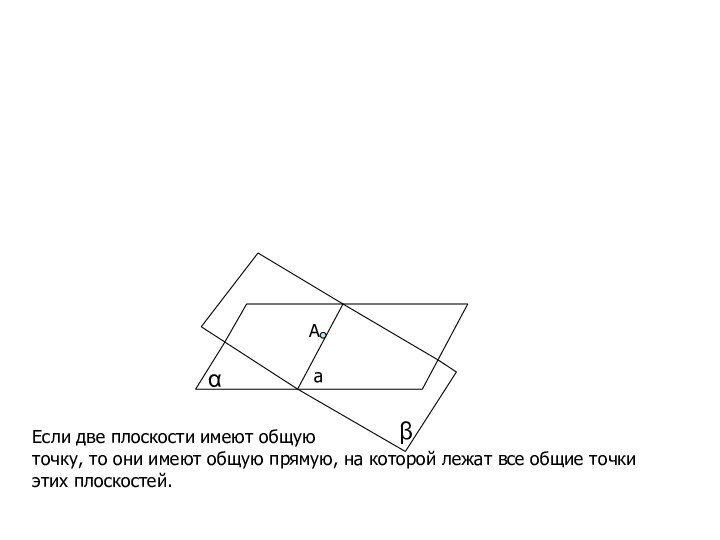
α
β
Если две плоскости имеют общую
точку, то они
имеют общую прямую, на которой лежат все общие точкиэтих плоскостей.
a
A
Слайд 21
Следствия из аксиом стереометрии.
Теорема 1.Через прямую и
не лежащую на ней точку проходит плоскость, и притом
только одна.
Слайд 23
Доказательство.
Возьмем точки Р a, Q a.По
А1 α, Р α,Q α, М α.
Так как Р α и Q α, то по А2 а α.Любая плоскость, проходящая через прямую а и точку М, проходит через точки М, P, Q. Следовательно, она совпадает с α, так как по А1 через точки M, P,Q проходит только одна плоскость.
Слайд 26
Доказательство
Возьмем точку N b. По Т1 α, а
α,N α. Так как N b,M b и N
α, М α,то по А2 b α. Итак, a α и b α.Любая плоскость, проходящая через a и b, проходит через N. Следовательно, она совпадает с α, так как по T1 через N и a проходит только одна плоскость.