Слайд 2
Актуальность темы:
- задача, исследуемая в данной
работе, как проблема, встречается в жизни, она
имеет практический интерес;
- сопутствующие теоретические наработки необходимы при изучении школьного курса математики, а так же для получения дальнейшего математического образования
Цели и задачи исследования:
- развитие склонности к познанию и исследования окружающего мира, умений проводить исследования, проходя последовательно все этапы;
- развитие творческих способностей при решении проблемных задач, умений анализировать и умений увидеть в проблеме удивительное и развитие способностей их разрешить;
- научиться доказывать гипотезы.
Слайд 3
Методы и материалы:
-мотивация исследовательской деятельности;
-постановка проблемы;
-сбор фактического материала;
-систематизация
и анализ полученного материала;
-выдвижение и проверка гипотез;
-доказательство или опровержение
гипотез.
Время ведения исследований: с 1.10.12г. по 8.02.13г
Характеристика личного вклада в решение избранной проблемы:
-проведены опыты по выявлению сравнительной характеристики вместимостей ёмкостей, выдвинуты гипотезы;
-установлены соответствующие зависимости между величинами;
-проведены исследования, доказательства и получены выводы.
Слайд 4
«Ни одно человеческое исследование не может быть
называться
истинной наукой, если оно не прошло
через математическое
доказательство».
Леонардо да Винчи
Великий французский архитектор Корбюзье как-то воскликнул: «Всё вокруг геометрия!». Сегодня уже в 21 столетии мы можем повторить это восклицание с ещё большим изумлением. В самом деле, посмотрите вокруг - всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики. Воистину, современная цивилизация - это Цивилизация Геометрии.
Слайд 5
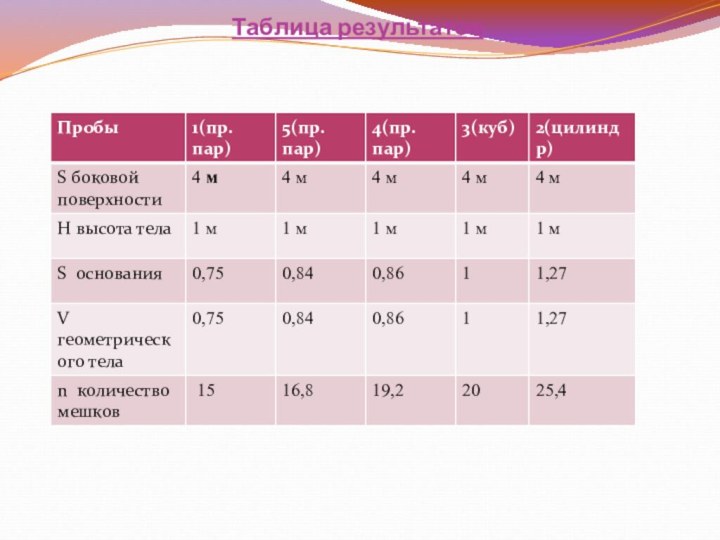
Геометрия возникла на основе практической деятельности людей.

В домашнем хозяйстве встречаемся с задачей – парадоксом.
Суть в том, что если высыпать зерно в ёмкость в форме прямоугольного параллелепипеда, то войдёт меньше зерна, чем в ёмкость цилиндрической формы. Полученное наблюдение в любом математике вызывает неподдельный интерес, поэтому будем её математически исследовать, «увидим» более общие проблемы, нежели та, которая отражена в условии задачи.
Задача:
Куплено 4 листа жести, длина и ширина каждой соответственно составляют 1м и 2м. Из них изготовлены ёмкости для зерна, потратив на каждую ёмкость по два листа данного размера: одна ёмкость в форме прямоугольного параллелепипеда (стороны основания 1.5м и 0,5м соответственно), а другая - цилиндрической формы, при этом на днища ёмкостей материал не расходуется. Высоты ёмкостей одинаковы и равны 1м. И не было предела удивлению, когда в ёмкость цилиндрической формы вошло 25,4 мешка зерна, а в ёмкость в форме прямоугольного параллелепипеда только 15 мешков. Почему такое возможно?
Слайд 6
При решении задачи рассматривались следующие проблемы:
1. Установить
зависимость между площадями оснований прямоугольного параллелепипеда и цилиндра и
их объёмами.
2. Как изменится вместимость ёмкости, если заменить ёмкость в форме прямоугольного параллелепипеда на ёмкость в форме куба.
3. За счёт чего получается такая разница в количестве высыпанных мешков?
4. Выявить самый оптимальный вариант решения задачи : при наименьшем расходе материала, соответственно - экономии денежных средств, изготовить ёмкость максимальной вместимости.
Слайд 8
Гипотезы, полученные в ходе исследования:
Гипотеза 1. За счёт
увеличения площади основания геометрического тела увеличивается и количество высыпаемых
зёрен в соответствующую ёмкость.
Гипотеза 2. Из всех тел в форме прямоугольного параллелепипеда наибольший объём имеет прямоугольный параллелепипед с размерами 1м* 1 м* 1 м, то есть -куб.
Гипотеза 3. Во сколько раз увеличивается площадь основания геометрического тела при неизменной высоте, во столько раз увеличивается его объём.
Слайд 9
Результаты исследования:
При изготовлении в быту ёмкостей из
металлических изделий им необходимо придавать цилиндрическую форму, чем форму
прямоугольного параллелепипеда. Это позволит нам изготовить ёмкость наибольшего объёма при экономии материала и денежных средств. Если ёмкость цилиндрической формы занимает больше места и вызывает неудобства в размещении по своей форме, то наиболее выгодным вариантом является куб.
Слайд 10
В перспективе:
Если рассмотреть геометрические тела, которые по своей
форме применимы на практике, то из них наибольший объём
при постоянстве площадей поверхностей имеет шар( рассматривается в приложении).
В жизни встречаем множество тел цилиндрической круглой формы. Люди давно научились строить не только дома – «коробки», но и круглой формы. Может, они имеют некоторые преимущества? Проведём исследование не только по вместимости, но и по энергоэкономичностью и теплоэффективности, что влияет на экологию окружающей среды.
Слайд 11
Сооружение круглых домов связывают с кельтами.
Круглые
дома в доисторическом селении Хирокития на Кипре (реконструкция)
Вигвам индейцев
Слайд 12
Первый круглый дом

Американский инженер и архитектор Ричард Фуллер (1895 - 1983).
Он первый создал математический алгоритм для расчета купола круглого дома. Он получил и патент на конструкцию купола на круглый дом.
Такой круглый дом обладает:
Малой массой при большом внутреннем пространстве дома.
Купол круглого дома устойчив к большим нагрузкам, причем, чем больше купол, тем прочнее конструкция круглого дома.
Круглый дом требует стандартных элементов для сборки купола, благодаря чему весь комплект круглого дома можно изготовить заранее на производстве.
Круглый дом при сборке не требует крана: строители могут передвигаться по ячейкам сетчатого купола.
Купол круглого дома обладают идеальной аэродинамической формой, благодаря чему круглые дома можно возводить в ураганных районах.
Круглый дом энергоэффективнее дома коробки: площадь наружных поверхностей круглого дома на 36% меньше. Использование отражающих материалов изнутри купола позволяют фокусировать инфракрасное тепловое излучение в центре дома.
Слайд 18
Круглые дома и фасады домов в Чебоксарах
Слайд 19
Круглые купольные дома будущего.
Вид внутри.
Слайд 21
Купольный дом— сферическое архитектурное сооружение, собранное из
металлических или деревянных балок, благодаря которой сооружение приобретает хорошие
несущие качества. По сути это совокупность треугольников, соединенных особым образом. Геометрическая симметрия порождает сочетание прочности и компактности. Форма купола получается благодаря особому соединению балок — в каждом узле сходятся три ребра, которые образуют правильный многогранник, вписанный в сферу.
Слайд 22
Основные отличия круглого дома
1.Простота и комфорт, компактность и
уют, рациональное использование пространства и практичность.
2.Нетрадиционные формы зданий позволяют
с пользой задействовать каждый квадратный метр жилья.
3.Сфера наилучшая форма для дома при ветровых и снеговых нагрузках.
4.Сфера имеет наибольший объем при наименьшей площади поверхности.
5.Минимальны материалоемкость, трудоемкость и время создания сферы.
6. Так как сфера изготавливается бесшовной, минимизируются теплопотери, отопительная система минимальная.
7. Все необходимое для изготовления сферы базируется на 2-3 машинах.
8.Не нужен ремонт кровли – крыши, ибо она не течёт.
9. Вопрос вентиляции – герметически закрывающееся отверстие вверху сферы.
10.В случае каких-либо природных катаклизмов сфера будет устойчивей
"прямоугольника"
Слайд 23
Несколько доводов в пользу
круглого дома:
Использование полезной площади
на 100%!
Полусфера — наиболее оптимальная форма для эффективного использования
полезной площади. Если полусферу переформовать в параллелепипед, то обнаружится, что потеряно от 40-60% пространства интерьера! При возведении круглого дома у вас уходит меньше материалов.
В круглом доме просто нет внешних углов, - которые являются местом особого промерзания из-за недостаточной конвекции — застое воздушных масс в углах , снижаются энергозатраты на отопление такого дома.
Не боится сквозняков, что влияет на тепловой баланс не только внутри здания, но и окружающей среды в природе.
Круглый дом можно вертеть на планируемой территории как заблагорассудится, не думая о параллельности... симметричности — он же — КРУГЛЫЙ!
Слайд 24
Выводы:
Круглый дом очень экономичен в эксплуатации. Благодаря аэродинамическим

свойствам купола уменьшается сопротивление ветру, нет зон низкого и
высокого давления, не отмечено выветривание тепла и сквозняки.
Нами на местности построек круглых домов не обнаружено????? Церковь в Чурашево???????
Почему же у нас не строят таких круглых домов? Именно это и заинтересовало нас, при выборе такой теме проекта. Мы выделили несколько причин, почему стоится так мало круглых домов:
1.Психологические причины - мы (люди) привыкли жить в квадратных и прямоугольных домах. У нас - соответствующая мебель, бытовая техника. Многим из нас "круглый" дом представляется смешным, но и напротив – для многих и многих купольный дом - красив. Прельщает большой внутренний объем купола .
2.Информационные причины - очевидны: из-за недостатка информации вот так просто взять и построить купольный дом не получится. Геодезический купол имеет простую, но специфическую геометрию, нюансам которой в строительных институтах и институтах архитектуры не учат.
Слайд 25
Итоги:
Итак, цилиндрическая форма дома становится все более востребованной,
и не исключено, что круглые дома станут «модными» по
всей России. Ведь основные преимущества круглых зданий, такие, как прочность и «экономия» площади под застройку, актуальны везде. Так что, может, идея не настолько уж и курьезна.
Разработка нашего проекта заинтересовала нас тем, что строительство круглых домов вывело бы наше строительство на новый уровень развития.
Наш проект будет интересен тем, кто думает связать свою жизнь со строительной специальностью, например, это архитектор, дизайнер, строитель и др.
Слайд 26
Ещё раз о телах
цилиндрической и
круглой формы
Скворечники
круглой формы лучше охраняют птиц от сквозняков.
Замена квадратных абажуров
на круглые экономят электроэнергию.
Купола православных церквей и мечетей тоже имеют круглую форму ( можно продолжить изучение).
Но… металлическая труба (профиль) имеет достоинства квадратного и прямоугольного сечения как строительный материал по сравнению круглыми:
- транспортировка, простота в работе, удобство их
обработки и соединения стыковочных швов,
- уменьшает общий вес конструкции, при этом обеспечив необходимый запас прочности.
В примере с профилем преимущества в использовании даёт не внутренний объём трубы, а в основном форма.