- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Золотое сечение в математике
Содержание
- 2. Принципы «золотого сечения» используются в математике,
- 3. Золотое сечение - деление отрезка на две
- 4. История золотого сечения В математике принцип «золотого
- 5. Если упростить задачу Эвклида, то отрезок линии
- 6. Золотое сечение тесно связано с числами Фибоначчи.
- 7. Рассмотрим взаимосвязь «золотого сечения с числами Фибоначчи:Числа,
- 8. Если какой-либо член последовательности Фибоначчи разделить на
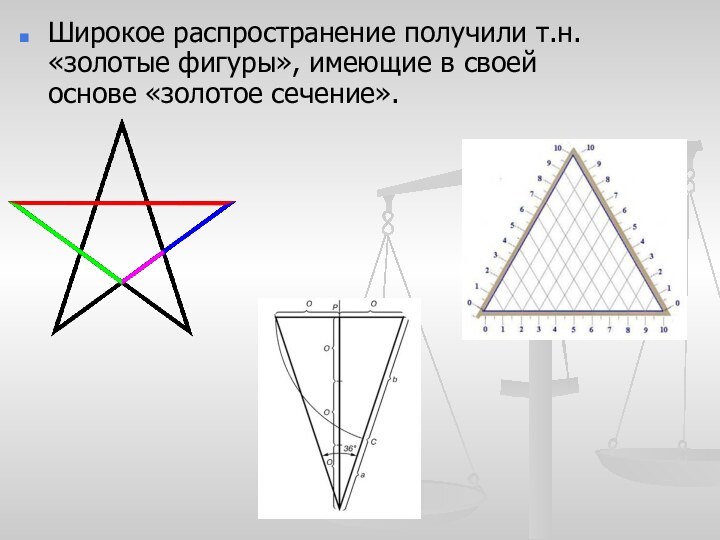
- 9. Широкое распространение получили т.н. «золотые фигуры», имеющие в своей основе «золотое сечение».
- 10. Последовательно отсекая от «золотых прямоугольников» квадраты до
- 11. Интерес человека к природе привёл
- 12. Рассматривая расположение листьев на общем стебле многих
- 13. Природа повторяет свои находки, как в малом,
- 14. Знакомство с принципами «золотого сечения», помогает видеть
- 15. Скачать презентацию
- 16. Похожие презентации
Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе архитектурных пропорций многих замечательных произведений мирового зодчества.














Слайд 3 Золотое сечение - деление отрезка на две части
таким образом, что большая его часть является средней пропорциональной
между всем отрезком и меньшей его частью.
Слайд 4
История золотого сечения
В математике принцип «золотого сечения»
впервые был сформулирован в «Началах» Эвклида, самом известном математическом
сочинении античной науки, написанном в III веке до н.э. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.Слайд 5 Если упростить задачу Эвклида, то отрезок линии АВ
будет считаться разделенным точкой С (которая ближе к точке
В) в «золотой пропорции», если отношение большей части а к меньшей b равно отношению всего отрезка с или (а+b) к большей части а, т.е. а : b = c : a. Результатом решения этой задачи является иррациональное число, приблизительно равняющееся 1,618, которое и называют золотым сечением, золотым числом или золотой пропорцией.Слайд 6 Золотое сечение тесно связано с числами Фибоначчи. Числа
0.618 и 0.382 являются коэффициентами последовательности Фибоначчи. На этой
пропорции базируются основные геометрические фигуры.
Слайд 7
Рассмотрим взаимосвязь «золотого сечения с числами Фибоначчи:
Числа, образующие
последовательность 1, 1, 2, 3, 5, 8, 13, 21,
34, 55, 89, 144, 233,... называются «числами Фибоначчи», а сама последовательность - последовательностью Фибоначчи. Суть последовательности Фибоначчи в том, что начиная с 1, 1 следующее число получается сложением двух предыдущих.Слайд 8 Если какой-либо член последовательности Фибоначчи разделить на предшествующий
ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального
значения 1.61803398875... и через раз то превосходящая, то не достигающая его.Слайд 9 Широкое распространение получили т.н. «золотые фигуры», имеющие в
своей основе «золотое сечение».
Слайд 10 Последовательно отсекая от «золотых прямоугольников» квадраты до бесконечности,
каждый раз соединяя противоположные точки четвертью окружности, можно получить
довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали. В настоящее время «спираль Архимеда» широко используется в технике.В гидротехнике по «золотой спирали» изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.
Слайд 11 Интерес человека к природе привёл к
открытию её физических и математических закономерностей. Красота природных форм
рождается во взаимодействии двух физических сил - тяготении и инерции. Золотая пропорция - это математический символ этого взаимодействия, поскольку выражает основные моменты живого роста: стремительный взлёт юных побегов сменяется замедленным ростом «по инерции» до момента цветения.Слайд 12 Рассматривая расположение листьев на общем стебле многих растений,
можно заметить, что между каждыми двумя парами листьев третья
расположена в месте «золотого сечения».«Золотую спираль» также можно заметить в созданиях природы. Например, расположение семечек в корзине подсолнечника. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнечника закручено 13 спиралей, в другую - 21. Отношение 13: 21 - отношение Фибоначчи.
Слайд 13 Природа повторяет свои находки, как в малом, так
и в большом. По золотым спиралям закручиваются многие галактики,
в частности и галактика Солнечной системы.Слайд 14 Знакомство с принципами «золотого сечения», помогает видеть гармонию
и целесообразность окружающих нас творений природы и человека. Можно
сделать выводы:во-первых, золотое сечение - это один из основных основополагающих принципов природы;
во-вторых, человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе.





























