Презентация на тему Скалярное произведение

аналогичные свойствам произведения чисел:

1.

2.

3.








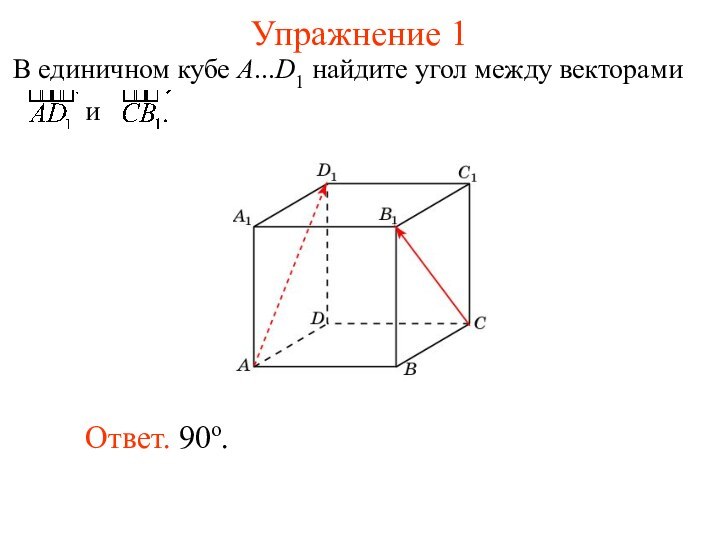
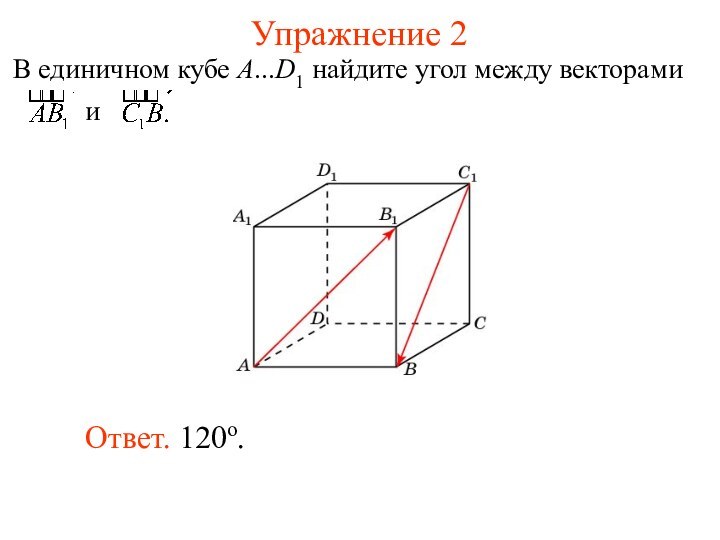
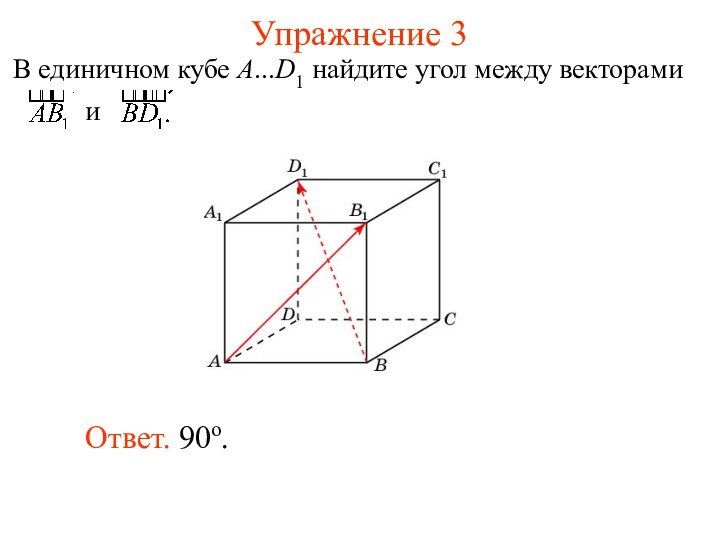
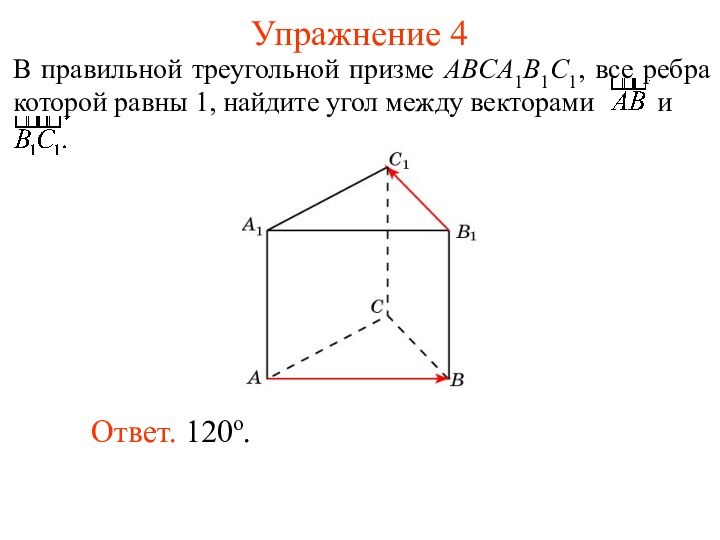
Используя формулу

Теорема. Скалярное произведение векторов , выражается формулой

A...D1 найдите угол между векторами
и

в) 90о;
г) 120о;

д) 150о.

Найдите скалярное произведение векторов:
а)

Ответ: а) 0;

б) 25;

в) 25;

г) 89;

д) 100.

2, 3) и (2, -1, 0).

Ответ: –4.

угол между ними: а) острый; б) тупой?
Ответ: а) Плюс;

б) минус.

векторов равно нулю?
Ответ: Если они перпендикулярны.

3, -1) и (1, -2, 4);

б)

б) ϕ = 45о.

Ответ: z = -2.

AB, AD, DC правильного тетраэдра с ребром 4. Найдите

Ответ: а) 2;

б) -2;

в) -2;

г) 1;

д) -1;

е) 0.

вектор:
а)
б)
в)
г) (0, 3, 4).
в) 180о, 90о,