1.2. Свойства движения
1.3.
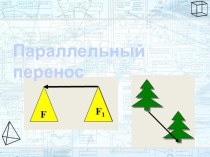
Параллельный перенос1.4. Центральная симметрия
1.5. Осевая симметрия
1.6. Поворот
ГЛАВА 2. ГОМОТЕТИЯ
2.1. Гомотетия
2.2. Свойства гомотетии
2.3. Гомотетичность окружностей
2.4. Композиция гомотетий
2.5. Поворотная гомотетия
ГЛАВА 3. Разные задачи из Всероссийских олимпиад школьников



![ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ГОМОТЕТИИ В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ ОЛИМПИАДНОГО УРОВНЯ Следствие 1.1.[6] При движении прямые переходят в прямые, полупрямые – в полупрямые,](/img/tmb/6/533002/4d2635f3ff569f17c061cbffc9b08d1a-720x.jpg)
![ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ГОМОТЕТИИ В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ ОЛИМПИАДНОГО УРОВНЯ Определение 1.4.[1] Паралелльный перенос или трансляция – частный случай движения, при котором](/img/tmb/6/533002/b630481d7f2a2ca27c187aec41ed233b-720x.jpg)
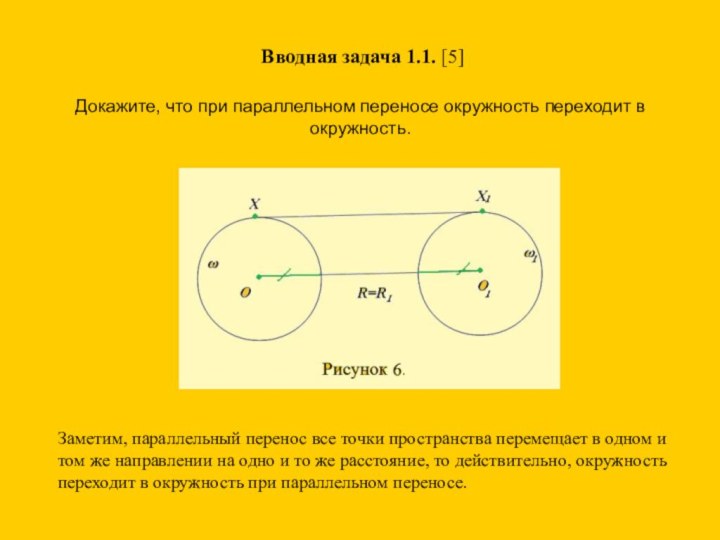

![ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ГОМОТЕТИИ В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ ОЛИМПИАДНОГО УРОВНЯ Определение 1.[1 ] Гомотетией называют преобразование плоскости, которое каждую точку X отображает](/img/tmb/6/533002/9919da2846514017bd5f705879fc88f7-720x.jpg)
![ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ГОМОТЕТИИ В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ ОЛИМПИАДНОГО УРОВНЯ Определение 2. [1] Две фигуры называются гомотетичными, если одна из них переходит](/img/tmb/6/533002/e64bf2fb284b18195056188aab372c67-720x.jpg)
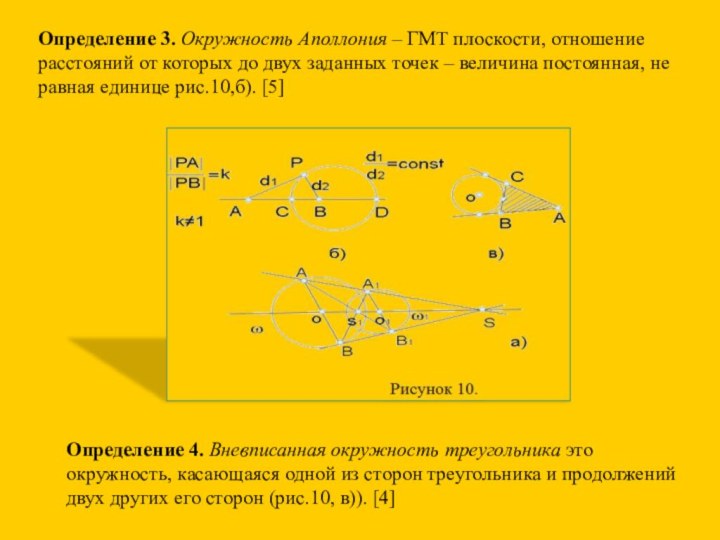
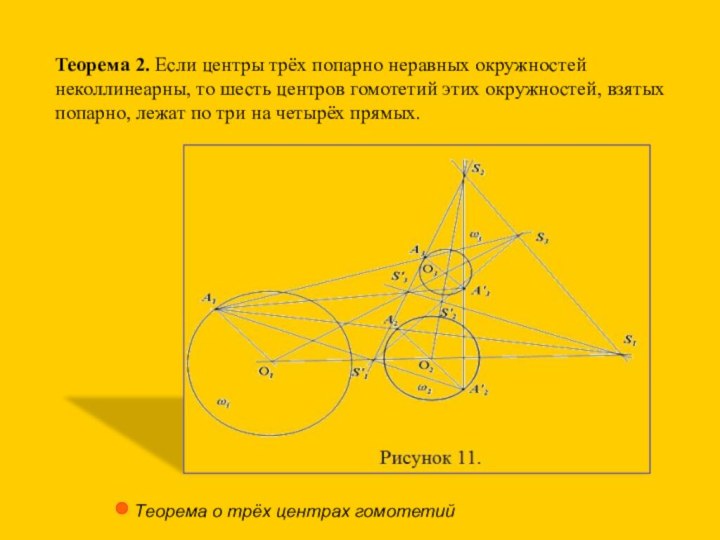
![ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ГОМОТЕТИИ В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ ОЛИМПИАДНОГО УРОВНЯ задача №871 из сборника «Всероссийские олимпиады школьников по математике 1993-2009: заключительные этапы»[1]Дан](/img/tmb/6/533002/80babd87f6167f77a05b9b9799922ad8-720x.jpg)