Презентация на тему Четырехугольники

Многоугольник

Выпуклый

Невыпуклый
Многоугольник называется
выпуклым, если он лежит
по одну сторону от каждой
прямой, проходящей через
две его соседние вершины

Трапеция


четырёхугольник, у

которого

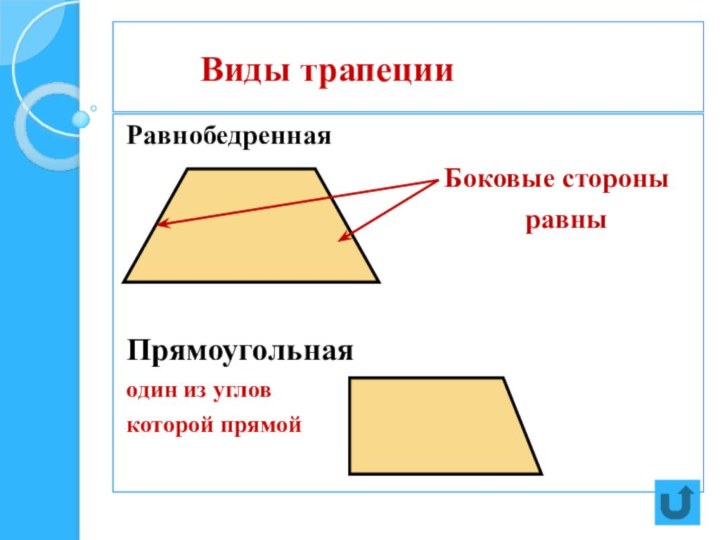
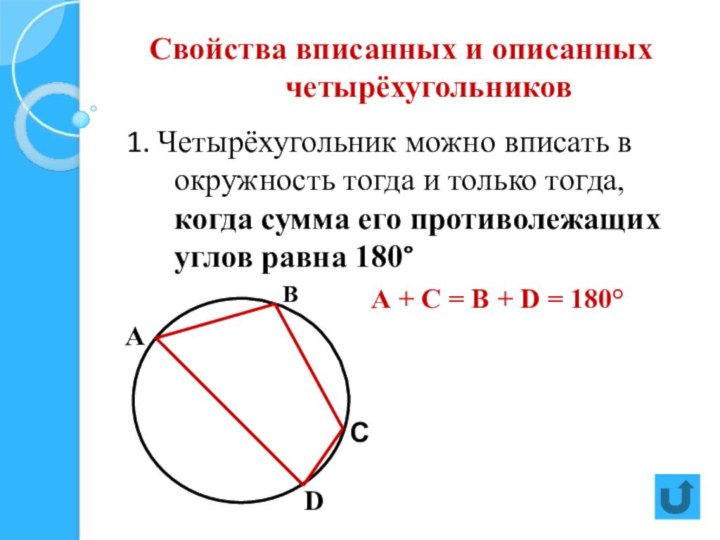
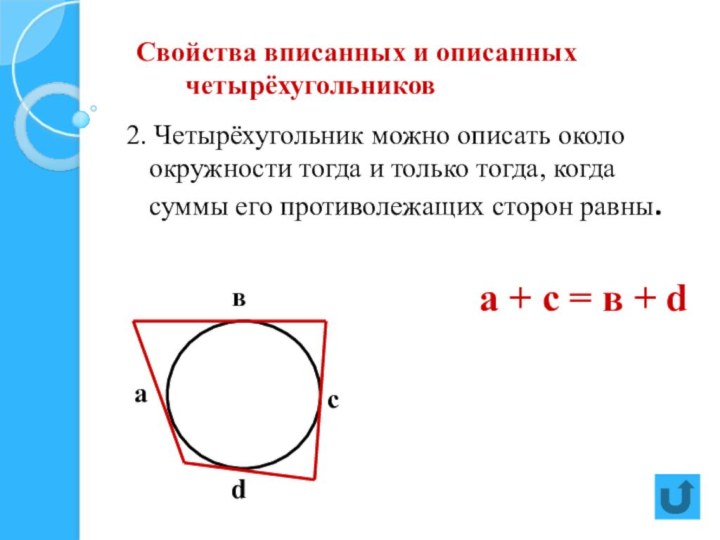
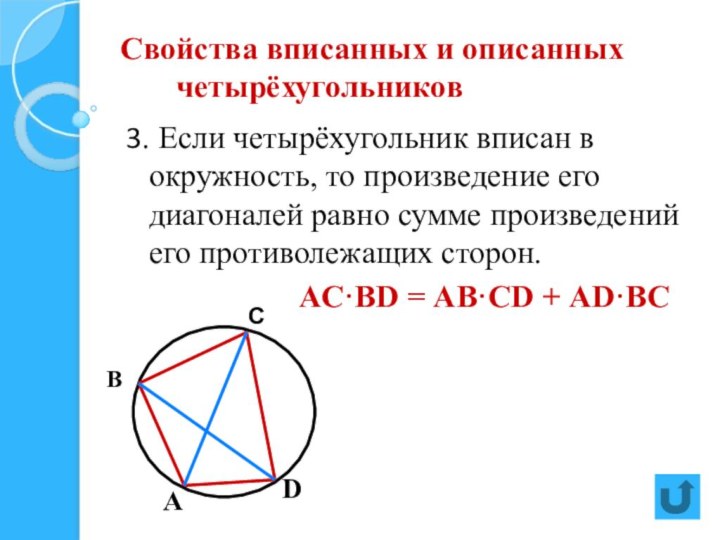
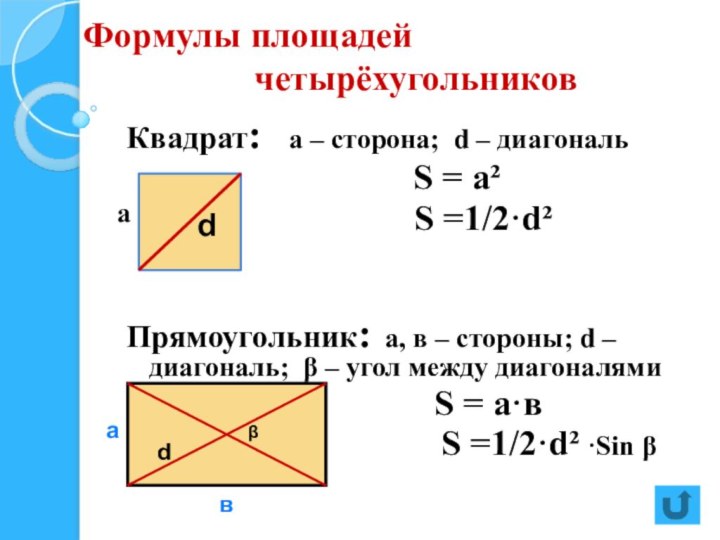
две стороны параллельны, а две другие стороны не параллельны

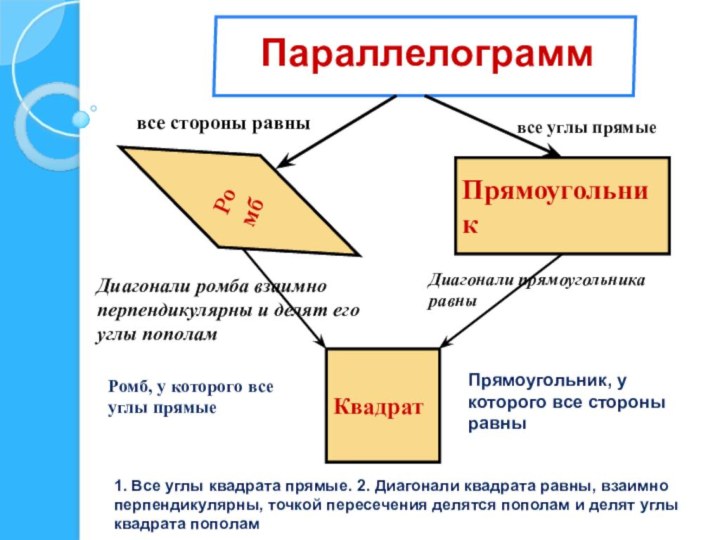
противоположные стороны попарно параллельны

противоположные стороны и противоположные углы равны.

В

А
2. Диагонали параллелограмма точкой пересечения делятся пополам.


3.Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180.


С А
4. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

Свойства параллелограмма

стороны равны
все углы прямые
Диагонали прямоугольника равны
Диагонали ромба

взаимно перпендикулярны и делят его углы пополам

Прямоугольник, у которого все стороны равны

Ромб, у которого все углы прямые

1. Все углы квадрата прямые. 2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам

стороны параллельны, а две другие стороны не параллельны.
Основания трапеции

– её параллельные стороны.
Боковые стороны трапеции – непараллельные, противолежащие стороны трапеции
Высота трапеции – это отрезок перпендикуляра от любой точки одного основания до её другого основания(или его продолжения)
Средняя линия трапеции – отрезок соединяющий середины боковых сторон трапеции.

Боковые стороны
равны


Прямоугольная
один из углов
которой прямой

и равна их полусумме.



2. У равнобокой трапеции углы при

основании (верхнем и нижнем) равны.

АD и ВС, точка Е- точка пересечения её диагоналей.

Тогда S∆АВЕ = S∆DСЕ
Данное свойство верно для любых трапеций.

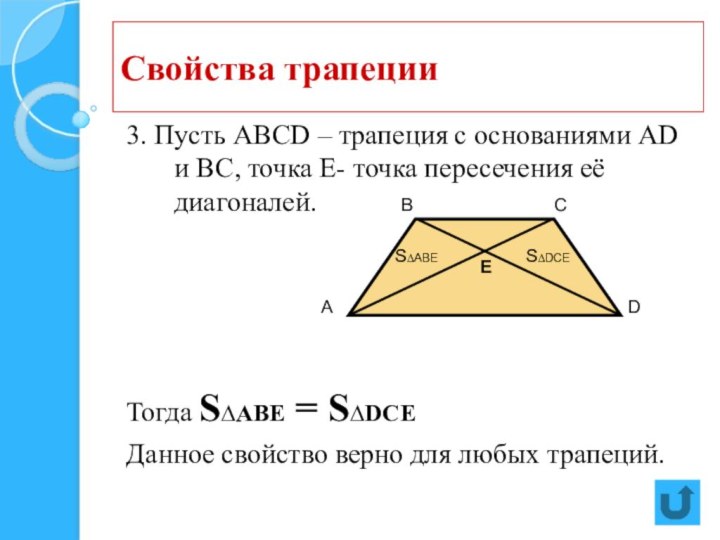
А

В

С

D

Е

S∆АВЕ

S∆DСЕ

четырёхугольников
1. Четырёхугольник можно вписать в окружность тогда и только

тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°

А

В

С

D

четырёхугольников
2. Четырёхугольник можно описать около окружности тогда и только

тогда, когда суммы его противолежащих сторон равны.

а + с = в + d

а

с

d

в

четырёхугольников
3. Если четырёхугольник вписан в окружность, то произведение его

диагоналей равно сумме произведений его противолежащих сторон.
АС·ВD = АВ·СD + АD·ВС

А

В

С

D

четырёхугольников
Квадрат: а – сторона;

d – диагональ
S = a²
S =1/2·d²


Прямоугольник: а, в – стороны; d – диагональ; β – угол между диагоналями
S = a·в
S =1/2·d² ·Sin β

а

d

а

в

β

d

α – угол между сторонами;

– диагонали;
β – угол между диагоналями;
- высоты, проведенные к сторонам а и b соответственно
S = a*
S = a·b·Sinα

S =

а

в

α

ha

hв

сторонами;

– диагонали;
h – высота
S = a·h

S = a²·Sinα

а

d1

d2

h

угол между сторонами;

– диагонали;
β – угол между диагоналями; h – высота;
m – средняя линия

S = m*h =

S =

в

а

h

m

– диагонали; β – угол

между диагоналями

d1

d2

β

S =