Презентация на тему по математике на тему Многогранники. Тела вращения

- угольников, лежащих в параллельных плоскостях и совмещаемых параллельным

Применение формы призмы в дизайне МР3

Треугольная призма

Четырёхугольная призма

основанию.
АВСD и A1B1C1D1- основания призмы
А A1; ВB1; СC1; DD1-боковые

А1D-диагональ призмы

А1В-диагональ боковой грани

Н=АА1=ВВ1=… высота прямой призмы равна боковому ребру

АА1 (АВСD); ВВ1 (АВСD)…

AA1B1B; BB1C1C; CC1D1D; DD1A1A – боковые грани (прямоугольники).

плоскостям основания
НО - высота призмы

BCDEFHGIKJ
Шестиугольная призма ABCDEFGIJKLH
Параллелепипед – призма, в основании которой лежит

Кубом называется прямоугольный параллелепипед, у которого все рёбра равны.

трёх его измерений: d 2 = a 2+b 2+c

Прямоугольный параллелепипед – прямой параллелепипед, основанием которого является прямоугольник.

Измерения прямоугольного параллелепипеда - это длины трёх рёбер, выходящих из одной вершины. HG = a HE = b HC = c DG = d – диагональ параллелепипеда

поверхность
Объём
Sполн = Sбок +2 Sосн
Sполн = Sбок + 2

V=Sосн∙ Н Sосн - площадь основания призмы, Н - высота.

- угольника (основания), точки, не лежащей в плоскости основания

Пирамиды в окружающем мире:

Египетские пирамиды

Пирамиды Майя

высота пирамиды, SO (ABC)
SK - высота

V=

S

O

A

B

C

Грань ASC перпендикулярна плоскости основания, SО- высота пирамиды и высота боковой грани ASC.

S

A

C

B

Грани ASC и ВSС перпендикулярны плоскости основания. АS-их общее боковое ребро. АS-высота пирамиды и боковых граней АSС и АSВ

правильным n-угольником, а основание высоты пирамиды совпадает с центром

Осью правильной пирамиды называется прямая, содержащая высоту пирамиды.

Апофемой правильной пирамиды называется высота боковой грани.

А

S

отрезок SО - высота,
прямая SО - ось,
SK – апофема.

пересечения медиан (высот и биссектрис), центр описанной и вписанной

Четырёхугольная

S

C

D

О

В

А

АВСD – квадрат;
О – точка пересечения диагоналей, центр описанной и вписанной окружностей.

Шестиугольная

ABCDEF - правильный шестиугольник; О - точка пересечения диагоналей AD, BE и FC (центр описанной и вписанной окружностей).

КОНУСА, ЦИЛИНДРА .
Архимед

не лежащих в одной плоскости и совмещающихся параллельным переносом,

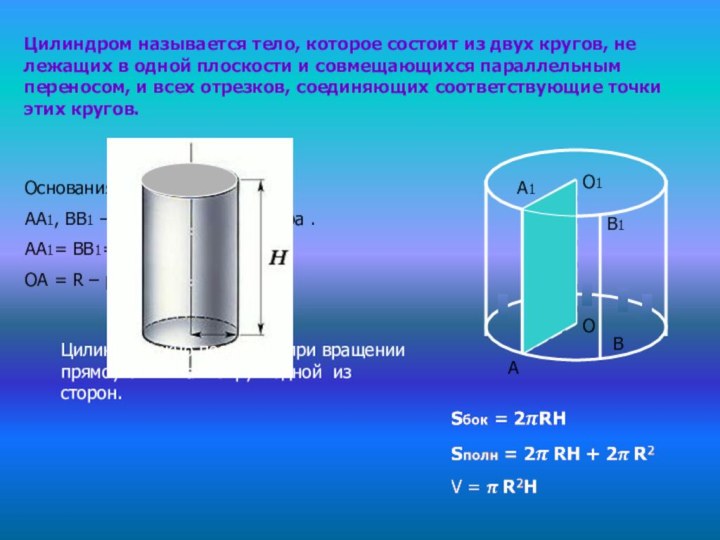
Основания – равные круги.
АА1, ВВ1 – образующие цилиндра .
АА1= ВВ1= ОО 1= Н – высота.
OA = R – радиус.

Цилиндр можно получить при вращении прямоугольника вокруг одной из сторон.

оси.
MNKL- прямоугольник.
KN-хорда, MN=H
Сечение плоскостью,
параллельной основаниям.
Сечение - круг,
равн ый основаниям.

лежащей в плоскости этого круга, и всех отрезков, соединяющих

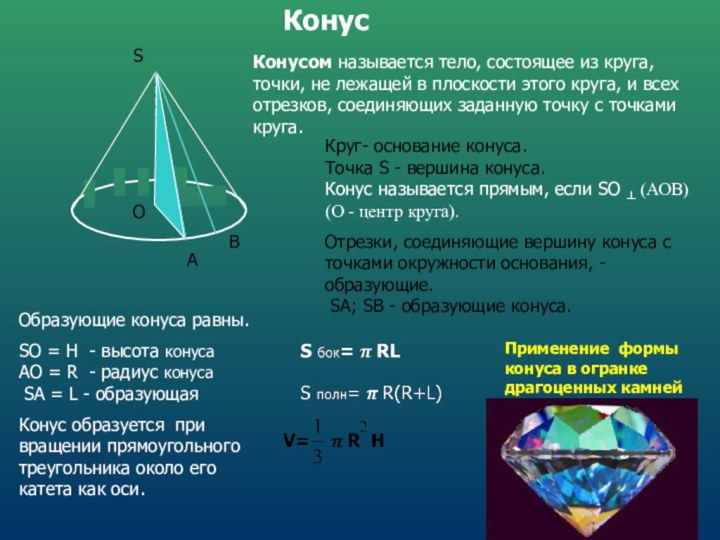
Круг- основание конуса.
Точка S - вершина конуса. Конус называется прямым, если SО ┴ (АОВ) (О - центр круга).
Отрезки, соединяющие вершину конуса с точками окружности основания, - образующие. SА; SВ - образующие конуса.

Образующие конуса равны.
SO = Н - высота конуса АО = R - радиус конуса SА = L - образующая
Конус образуется при вращении прямоугольного треугольника около его катета как оси.

Применение формы конуса в огранке драгоценных камней

заданной точки О на расстоянии, не большем данного расстояния

При вращении полукруга около его диаметра получаем ШАР.

Сфера является поверхностью шара.

О - центр шара,
ОА = R - радиус шара,
точки Р, М - полюса шара,
Прямая РМ - ось шара.

(Объём шара)

Цилиндр
Призма