- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тетраэдр и Параллелепипед
Содержание
- 2. Содержание:1)Титульный лист2)Определение тетраэдра и его свойства3)Построение тетраэдра4)Формула объема тетраэдра5)Определение параллелепипеда его свойства и типы6)Построение параллелепипеда
- 3. Многогранник составлен из четырех
- 4. Рассмотрим произвольный треугольник АВС и точку D,не
- 5. Объем тетраэдра, формула. Объем тетраэдра — равен
- 6. Определение:Параллелепипедшестигранник, противоположные грани которого попарно параллельны. П.
- 7. Параллелепипед симметричен относительно середины его диагонали. Любой
- 8. Рассмотрим два равных параллелограмма ABCD и A1B1C1D1
- 9. АDBCA1D1C1B1Параллелограммы, из которых составлен параллелепипед называют гранями.Их
- 10. Скачать презентацию
- 11. Похожие презентации







Слайд 2
Содержание:
1)Титульный лист
2)Определение тетраэдра и его свойства
3)Построение тетраэдра
4)Формула объема
тетраэдра
Слайд 3 Многогранник составлен из четырех равносторонних
треугольников. Каждая его вершина является вершиной трех треугольников. Сумма
плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.Определение:
Свойства
Тетраэдр.
1)Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
2)Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
3)Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
4)Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
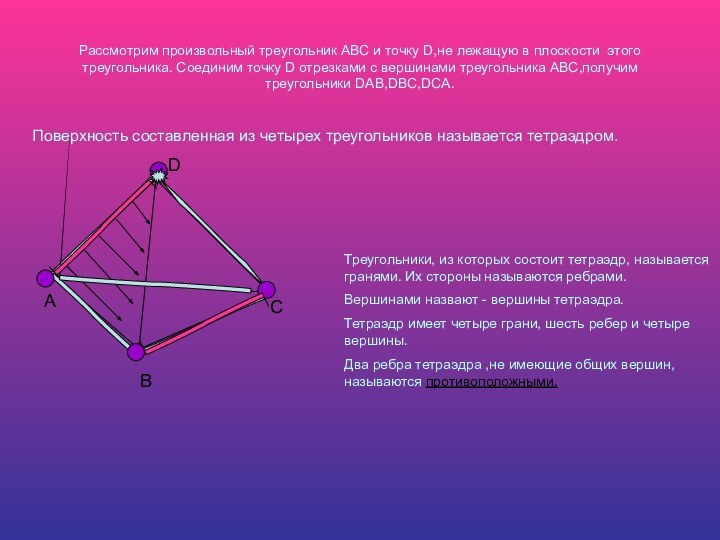
Слайд 4 Рассмотрим произвольный треугольник АВС и точку D,не лежащую
в плоскости этого треугольника. Соединим точку D отрезками с
вершинами треугольника ABC,получим треугольники DAB,DBC,DCA.Поверхность составленная из четырех треугольников называется тетраэдром.
Треугольники, из которых состоит тетраэдр, называется гранями. Их стороны называются ребрами.
Вершинами назвают - вершины тетраэдра.
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины.
Два ребра тетраэдра ,не имеющие общих вершин, называются противоположными.
А
B
C
D
Слайд 5
Объем тетраэдра, формула.
Объем тетраэдра — равен дроби в
числителе которой корень квадратный из двух в знаменателе двенадцать,
помноженной на куб длины ребра тетраэдраV= √2/12*a3
Вывод формулы объема тетраэдра.
Объем тетраэдраОбъем тетраэдра расчитывается по классической формуле объема пирамидыОбъем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставить высоту тетраэдраОбъем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
Слайд 6
Определение:
Параллелепипед
шестигранник, противоположные грани которого попарно параллельны. П. имеет
8 вершин, 12 рёбер; его грани представляют собой попарно
равные параллелограммы. П. называется прямым, если его боковые ребра перпендикулярны к плоскости основания (в этом случае 4 боковые грани— прямоугольники); прямоугольным, если этот П. прямой и основанием служит прямоугольник (следовательно, 6 граней — прямоугольники); П., все грани которого квадраты, называется кубом. Объём П. равен произведению площади его основания на высоту .Типы параллелепипеда:
Прямоугольный параллелепипедПрямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники;
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники;
КубКуб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
Слайд 7
Параллелепипед симметричен относительно середины его диагонали.
Любой отрезок
с концами, принадлежащими поверхности параллелепипеда и проходящий через середину
его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.Противолежащие грани параллелепипеда параллельны и равны.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы
Прямой параллелепипед
Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
Объем V=Sо*h
Свойства
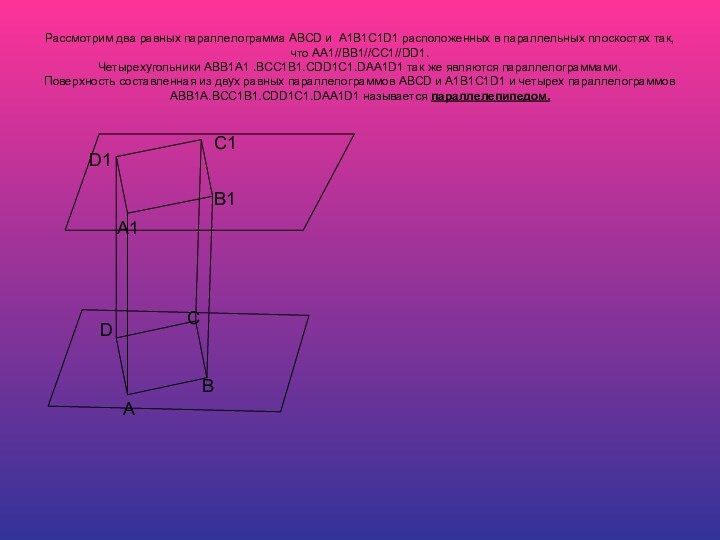
Слайд 8 Рассмотрим два равных параллелограмма ABCD и A1B1C1D1 расположенных
в параллельных плоскостях так, что AA1//BB1//CC1//DD1. Четырехугольники ABB1A1 .BCC1B1.CDD1C1.DAA1D1 так
же являются параллелограммами. Поверхность составленная из двух равных параллелограммов ABСD и A1B1C1D1 и четырех параллелограммов ABB1A.BCC1B1.CDD1C1.DAA1D1 называется параллелепипедом.D1
D
A
B
C
B1
C1
A1
Слайд 9
А
D
B
C
A1
D1
C1
B1
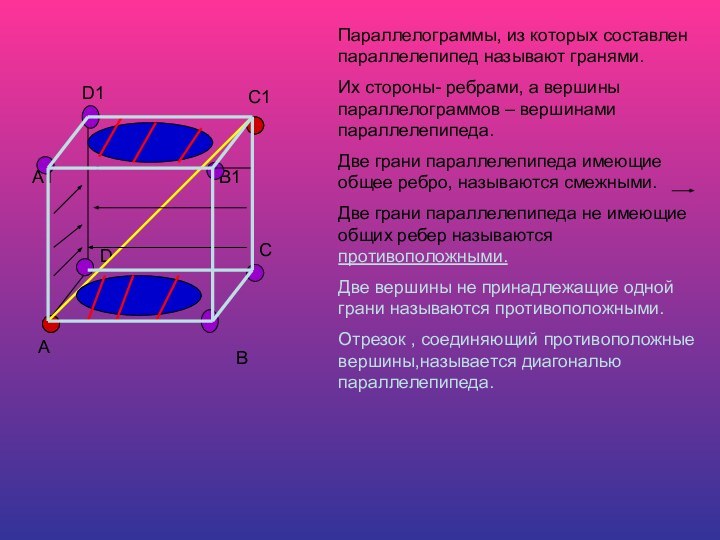
Параллелограммы, из которых составлен параллелепипед называют гранями.
Их стороны-
ребрами, а вершины параллелограммов – вершинами параллелепипеда.
Две грани
параллелепипеда имеющие общее ребро, называются смежными. Две грани параллелепипеда не имеющие общих ребер называются противоположными.
Две вершины не принадлежащие одной грани называются противоположными.
Отрезок , соединяющий противоположные вершины,называется диагональю параллелепипеда.