- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к интегрированному уроку по химии и математики на тему Решение задач на сплавы и смеси
Содержание
- 2. Тема урока: «Решение задач на растворы и сплавы»
- 3. Взаимосвязь между математикой и химией
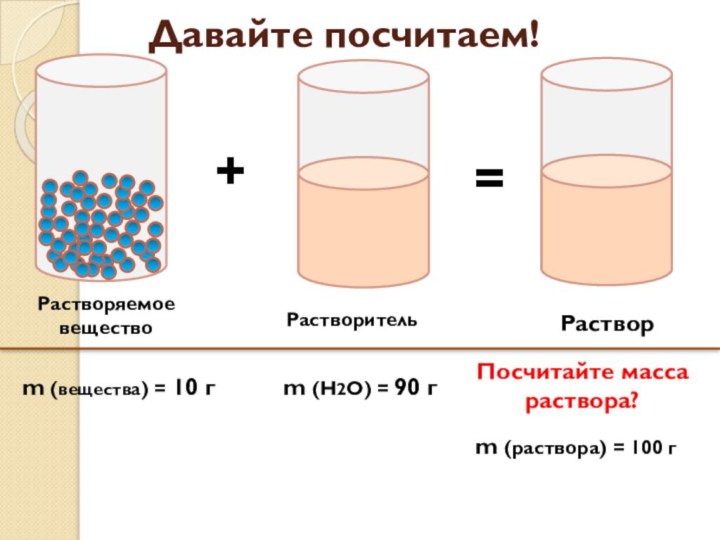
- 4. Из чего состоит раствор?Растворяемое веществоРастворитель+=РастворКак узнать какую часть или процент в растворе занимает вещество и растворитель?
- 5. Давайте посчитаем!m (раствора) = 100 г Посчитайте масса раствора?
- 6. Произведём расчёт в процентахω (вещества) = 10%
- 7. Решим задачу:Определить массу сахара, содержащегося в 300
- 8. Решение задачи:m (в-ва)= ω (в-ва) * m
- 9. Терминология: процентное содержание вещества; концентрация вещества; массовая доля вещества. Всё это синонимы!!!Необходимая формула:
- 10. Способы решения задач на сплавы и растворы:алгебраический;арифметический;
- 11. Решим задачи разными способами на растворы:1 способ: метод «стаканчиков»2 способ: метод «креста»
- 12. Решим задачу 2 способами:Задача №1: «Имеется 30
- 13. Решим задачу методом «стаканчиков»Имеется 30 кг 26%
- 14. Решение:7,8 + 0,5х = (30+х)· 0,47,8 +
- 15. Решим задачу методом «креста» Имеется 30 кг
- 16. Решим задачи разными способами на сплавы:1 способ: метод «стаканчиков»2 способ: метод «креста»
- 17. Решим задачу 2 способами:Задача №2. Имеется два
- 18. Решим задачу методом «стаканчиков»
- 19. Задача 2. Имеется два сплава меди и
- 20. Задача 2. Имеется два сплава меди и
- 21. Задача 2. Имеется два сплава меди и
- 22. Задача 2. Имеется два сплава меди и
- 23. Задача 2. Имеется два сплава меди и
- 24. Задача 2. Имеется два сплава меди и
- 25. Задача 2. Имеется два сплава меди и
- 26. Задача 2. Имеется два сплава меди и
- 27. Решим задачу методом «креста»
- 28. Решение:72%80%75%35х г800-х гЗадача 2. Имеется два сплава
- 29. Решите самостоятельно задачи:Задача1. В сосуд, содержащий 7 литров
- 30. Решим задачу методом «стаканчиков» +=7л14% 7л0%14лХ %Тогда
- 31. Решите самостоятельно задачи:Задача 2. Даны два
- 32. Решим задачу методом «стаканчиков» +=300г20% 200г4%500 гХ %Тогда 300*20 +200*40 = 500*х, то х =28%Ответ: 28
- 33. Решите самостоятельно задачи:Задача 3. Смешали 4 литра
- 34. Задача 4. Первый сплав содержит 10% меди,
- 35. ЗаключениеМы рассмотрели несколько различных методов решения задач
- 36. Скачать презентацию
- 37. Похожие презентации
Тема урока: «Решение задач на растворы и сплавы»



































Слайд 4
Из чего состоит раствор?
Растворяемое вещество
Растворитель
+
=
Раствор
Как узнать какую часть
или процент в растворе занимает вещество и растворитель?
Слайд 6
Произведём расчёт в процентах
ω (вещества) = 10%
ω
(H2O) = 90%
Всего раствора 100%
ω (в-ва) –
массовая доля вещества в раствореm (в-ва) – масса растворенного вещества в растворе
m (р-ра) – масса раствора
Слайд 7
Решим задачу:
Определить массу сахара, содержащегося в 300 г
15%-ного раствора.
х г 300 гω (в-ва) = 15%
растворитель
растворенное вещество
раствор
Слайд 8
Решение задачи:
m (в-ва)= ω (в-ва) * m (р-ра)
100%
m (в-ва)=15% * 300 г = 45 г
100%
Ответ: 45 г сахара содержится в 300 г 15%-ного раствора.
Слайд 9
Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества.
Всё это синонимы!!!
Необходимая формула:
Слайд 10
Способы решения задач на сплавы и растворы:
алгебраический;
арифметический;
графический;
способ расчета по формуле;
при помощи универсальной таблицы;
метод
«креста» (конверт Пирсона);метод «рыбки» (старинный метод);
метод «стаканчиков»;
при помощи прямоугольников и др.
Слайд 11
Решим задачи разными способами на растворы:
1 способ: метод
«стаканчиков»
2 способ: метод «креста»
Слайд 12
Решим задачу 2 способами:
Задача №1: «Имеется 30 кг
26% го раствора соли. Требуется получить 40% раствор соли.
Сколько кг 50% раствора соли нужно добавить?»
Слайд 13
Решим задачу методом «стаканчиков»
Имеется 30 кг 26% го
раствора соли. Требуется получить 40% раствор соли. Сколько кг
50% раствора соли нужно добавить?1 р-р 2 р-р 3 р-р
30· 26% х · 50% (30+х)· 40%
100% 100% 100%
7,8 + 0,5х = (30+х)· 0,4
26%
30 кг
50%
40%
Х кг
(30+х) кг
Слайд 14
Решение:
7,8 + 0,5х = (30+х)· 0,4
7,8 + 0,5х
= 12 + 0,4х
0,5х-0,4х=12-7,8
0,1х=4,2
х=4,2/0,1
х=42
Ответ: 42 кг 50% раствора соли
нужно добавить.
Слайд 15
Решим задачу методом «креста»
Имеется 30 кг 26% го
раствора соли. Требуется получить 40% раствор соли. Сколько кг
50% раствора соли нужно добавить?26% 10 30 кг
40
50% 14 х кг
10 = 30
14 Х
10х=420
Х=42
Ответ: 42 кг 50% раствора соли нужно добавить.
Слайд 16
Решим задачи разными способами на сплавы:
1 способ: метод
«стаканчиков»
2 способ: метод «креста»
Слайд 17
Решим задачу 2 способами:
Задача №2. Имеется два сплава
меди и олова. Один сплав содержит 72% меди, а
другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 19 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 20 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 21 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 22 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 23 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 24 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 25 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Слайд 26 Задача 2. Имеется два сплава меди и олова.
Один сплав содержит 72% меди, а другой 80% меди.
Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?Решение:
1)
Ответ:500 г, 300 г.
Слайд 28
Решение:
72%
80%
75%
3
5
х г
800-х г
Задача 2. Имеется два сплава меди
и олова. Один сплав содержит 72% меди, а другой
80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?1) 5 = х
3 800-х 2) 800-500=300 г
3х=5(800-х) Ответ: масса меди 500 г, масса олова 300 г.
3х=4000-5х
3х+5х=4000
8х=4000
х=4000/8
х=500
Слайд 29
Решите самостоятельно задачи:
Задача1.
В сосуд, содержащий 7 литров 14
процентного
водного раствора
некоторого вещества, добавили 7 литров
воды. Сколько процентов составляет
концентрация получившегося
раствора?
Слайд 30
Решим задачу методом «стаканчиков»
+
=
7л
14%
7л
0%
14л
Х %
Тогда 7л*14%
+7л*0% = 14л*х
, то х =
,х = 7
Ответ: 7
Слайд 31
Решите самостоятельно задачи:
Задача 2.
Даны два куска с
различным содержанием олова. Первый, массой 300г, содержит 20% олова.
Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?
Слайд 32
Решим задачу методом «стаканчиков»
+
=
300г
20%
200г
4%
500 г
Х %
Тогда
300*20 +200*40 = 500*х
, то х =
28%
Ответ: 28
Слайд 33
Решите самостоятельно задачи:
Задача 3. Смешали 4 литра 15-процентного
водного раствора некоторого вещества с 6 литрами 25-процентного водного
раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?Решение:
Ответ: 21%.
15%
25%
х%
(25–х)%
(х–15)%
4 л
6 л
Слайд 34 Задача 4. Первый сплав содержит 10% меди, второй
— 40% меди. Масса второго сплава больше массы первого
на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.Решение:
(кг) — 1-й сплав;
(кг) — 2-й сплав;
(кг) — 3-й сплав.
10%
40%
30%
10%
20%
х кг
(х+3) кг
1)
2)
3)
Ответ: 9 кг.
Решите самостоятельно задачи:
Слайд 35
Заключение
Мы рассмотрели несколько различных методов решения задач на
растворы и сплавы в математике.
При этом практически было
доказано, что прийти к верному ответу задачи можно, используя любой из рассмотренных выше способов решения. Каждый из рассмотренных методов опирается на знание понятий «массовая доля вещества в растворе», «концентрация вещества» и «процентное содержание вещества в растворе».
Определили, что знания по химии помогают решать задачи из ОГЭ по математике.