Слайд 2
Математика и
живопись
« В чистой
математике
живет всегда художник :
архитектор и даже поэт ».
Принсгейм А.
Слайд 3
Математика – царица всех наук, символ мудрости. Красота
математики среди наук недосягаема, а красота является одним из
связующих звеньев науки и искусства. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.
Слайд 4
Цель работы
Исследование связи математики и живописи, привлечение
учащихся к математике, к ее свойствам и законам.
Задачи
Для достижения
заданной цели необходимо решить следующие задачи :
1) Изучить методическую, научно-популярную и тематическую литературу.
2) Используя литературу выбрать наиболее интересных и увлекательных примеров связи математики и живописи..
Слайд 5
Актуальность темы : настоящий математик должен быть настолько
же творческим человеком, как художник или музыкант;
необходимо увлечь и
заинтересовать необычностью ситуации, жизненно- практической ценностью, неочевидностью ответа на поставленный вопрос.
Краткое содержание :
В работе на примерах показана связь математики с живописью.
Слайд 7
Существуют ли объективные законы прекрасного?
Нельзя отрицать заглавную роль
симметрии в природе, которая обязана своим существованием вечному закону
природы - закону тяготения.
В основе основ музыки и архитектуры- гамме и пропорции – лежит математика, в частности ряд золотого сечения.
В изобразительном искусстве используется общая теория перспективы.
Слайд 8
Золотое сечение
- (золотая пропорция, деление в крайнем и
среднем отношении) — деление непрерывной величины на две части в
таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
«И, поистине, живопись – это наука и законная дочь природы, ибо она порождена природой…»
Леонардо да Винчи
Слайд 9
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание
исследователей, которые обнаружили, что композиция рисунка основана на золотых
треугольниках, являющихся частями правильного звездчатого пятиугольника.
Слайд 11
Золотые пропорции нередко обнаруживаются в выдающихся памятниках средневековья
и нового времени, таких как, например, Собор парижской богоматери
(ранняя французская готика 1163-1345) и Тадж-Махал (индийская архитектура 1630- 1652).
Слайд 12
“Симметрия, как бы широко или узко мы не
понимали это слово, есть идея, с помощью которой человек
пытался объяснить и создать порядок, красоту и совершенство"
Герман Вейль
Слайд 13
Геометрия орнаментов, бордюров, паркетов.
Слайд 14
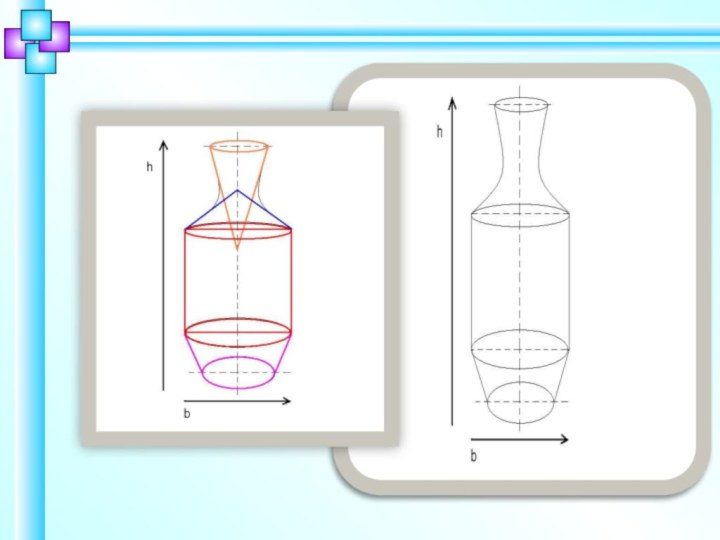
Связь математики и изобразительного искусства при конструктивном построении
натюрморта.
Натюрморт (фр. nature morte — букв. «мертвая природа») — изображение
неодушевлённых предметов в изобразительном искусстве, в отличие от портретной, жанровой, исторической и пейзажной тематики.
Слайд 16
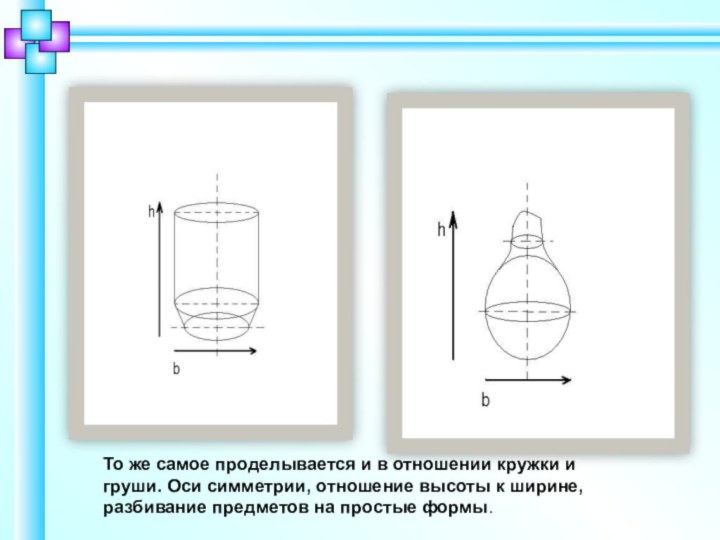
То же самое проделывается и в отношении кружки
и груши. Оси симметрии, отношение высоты к ширине, разбивание
предметов на простые формы.
Слайд 17
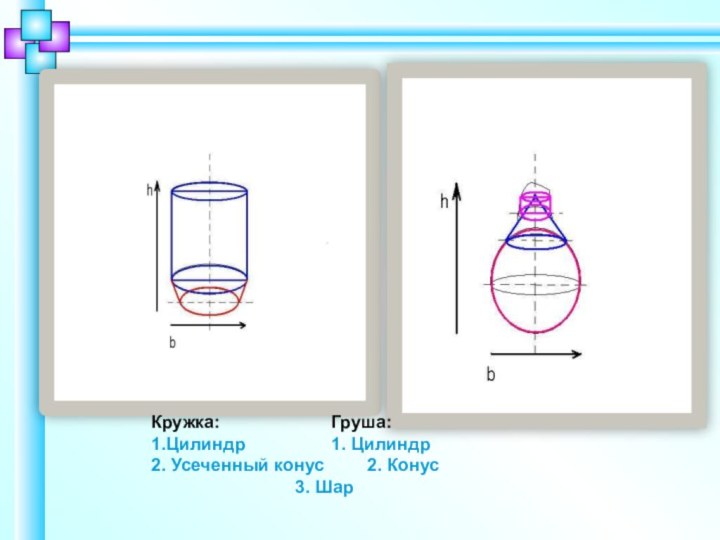
Кружка: Груша:
1.Цилиндр 1. Цилиндр
2. Усеченный конус 2. Конус
3. Шар
Слайд 18
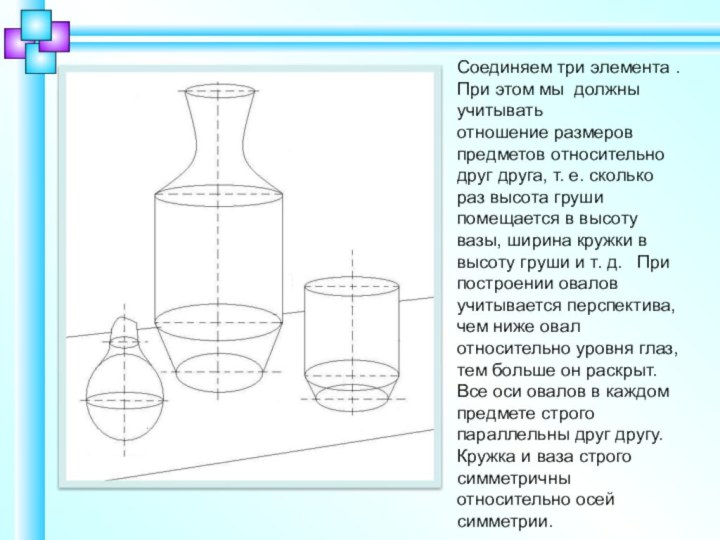
Соединяем три элемента . При этом мы должны
учитывать
отношение размеров предметов относительно друг друга, т. е. сколько
раз высота груши помещается в высоту вазы, ширина кружки в высоту груши и т. д. При построении овалов учитывается перспектива, чем ниже овал относительно уровня глаз, тем больше он раскрыт. Все оси овалов в каждом предмете строго параллельны друг другу. Кружка и ваза строго симметричны относительно осей симметрии.
Слайд 20
Использование идеи прямоугольных
координат в живописи.
Способ рисования с
натуры через стекло с нанесённой на него квадратной сеткой.
Гравюра
Дюрера.
Слайд 21
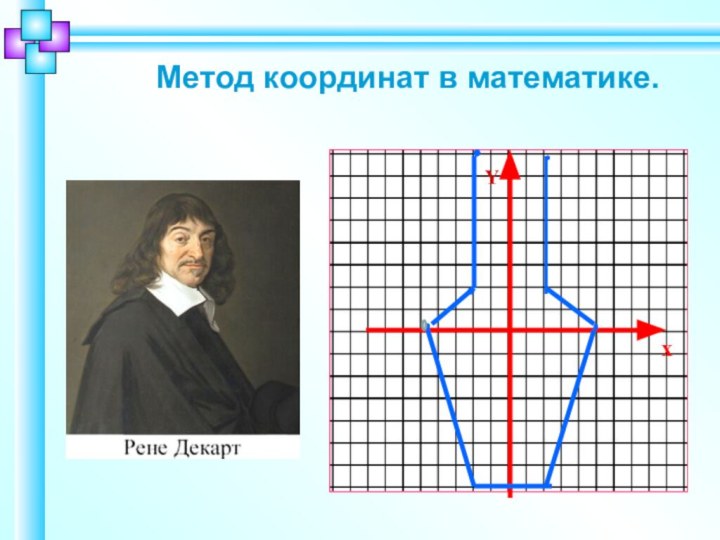
Метод координат в математике.
х
Y
Слайд 22
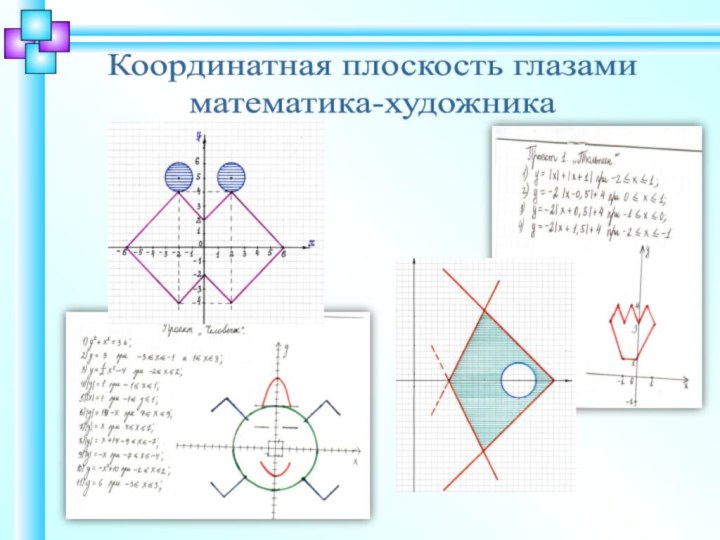
Координатная плоскость глазами
математика-художника
Слайд 23
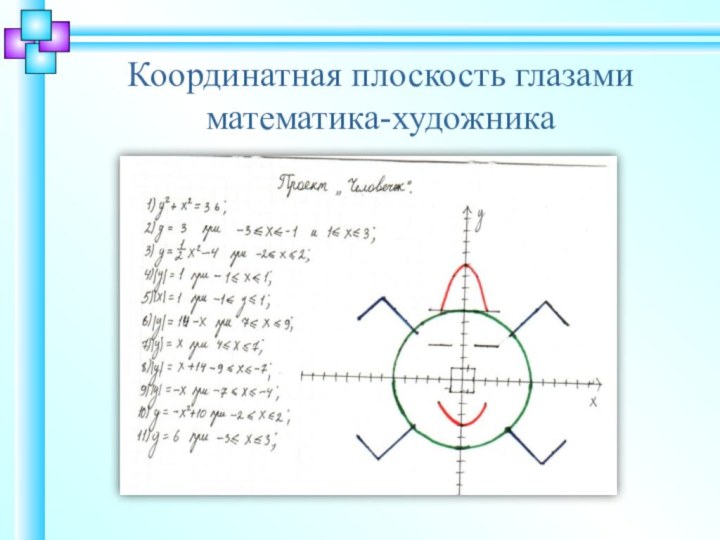
Координатная плоскость глазами
математика-художника
Слайд 24
Заключение:
Примеры взаимопроникновения математики в живопись и наоборот
можно приводить бесконечно…И чем дальше этим занимаешься, тем увлекательнее
становится такая работа. Но даже приведенных примеров, я думаю, достаточно для того, чтобы согласиться со словами Бертрана Рассела:
«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Слайд 25
«Потребность красоты и творчества, воплощающего ее, - неразлучна
с человеком, и без нее человек, быть может,
не захотел бы жить на свете».
Ф. М. Достоевский
Слайд 26
Над проектом работали:
Абрамов Александр
Абдуллаев Артур
Кубанова Ангелина
Новожилов Евгений Пестов Антон
Руководитель проекта
Абдуллаева Е.С.