четность, нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать функцию в бесконечности,
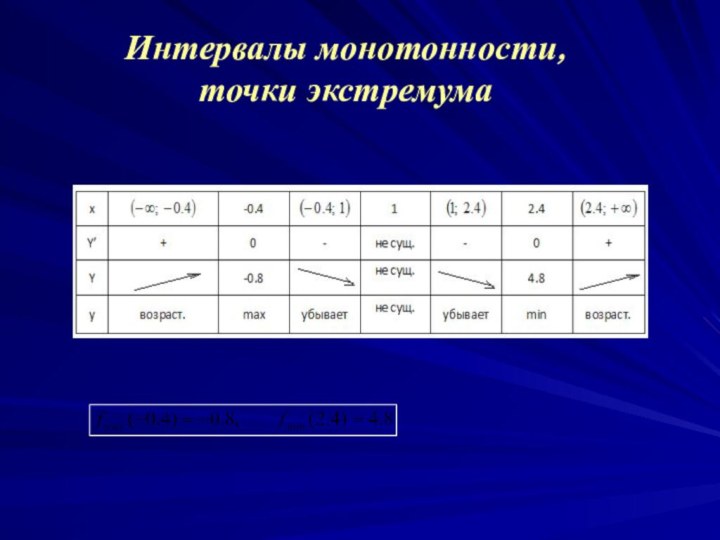
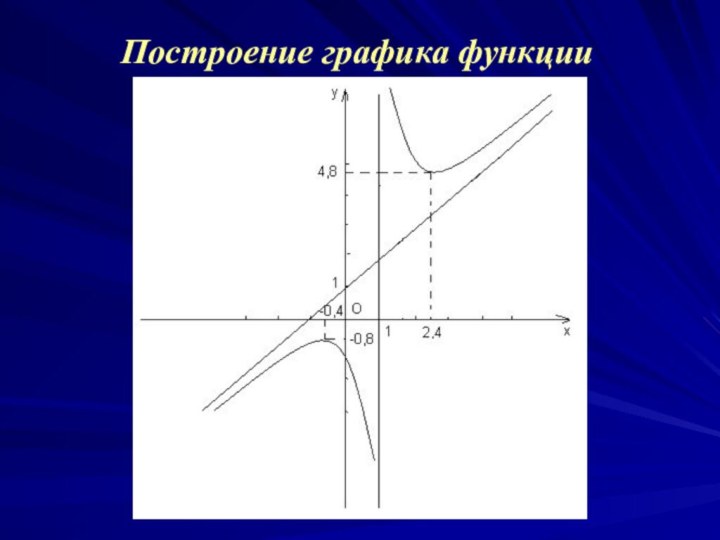
найти наклонные асимптоты.5. Найти интервалы монотонности, точки экстремума.
6. Найти интервалы выпуклости, точки перегиба.
7. Найти точки пересечения с осями координат (по возможности).
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ