Презентация на тему Divide et impera. Metodei şi aplicaţii

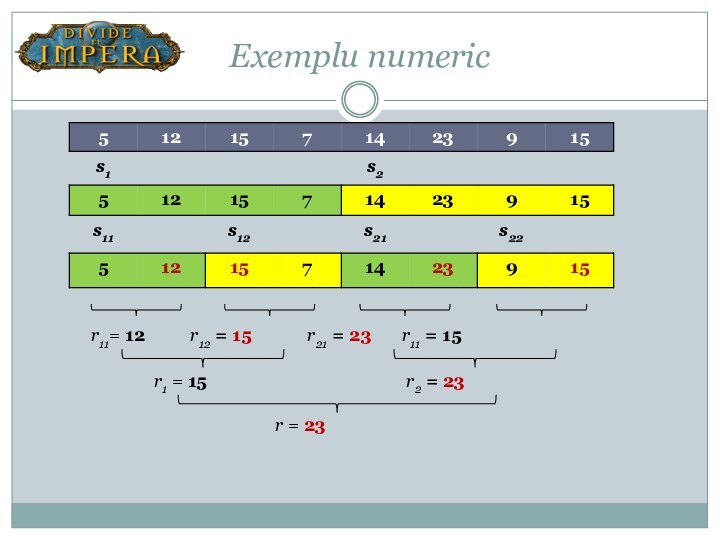
problemei de rezolvat în două sau mai multe probleme

similare celei iniţiale, dar de dimensiune mai mică şi apoi combinarea soluţiilor pentru a creea o soluţie a problemei iniţiale.
Procedeul se reia pentru fiecare din subproblemele obţinute până când (în urma descompunerilor repetate) se ajunge la probleme ce admit rezolvare imediată.
OBS: Deoarece problemele rezultate sunt similare celei iniţiale, metoda se poate exprima recursiv, dar admite şi varianta iterativă.

acelaşi tip, dar de dimensiune mai mică;
Impera: Se rezolvă

fiecare dintre subprobleme – direct dacă acestea sunt simple – sau continuă cu divide prin reducerea acestora la alte subprobleme, recursiv;
Impera: Se combină soluţiile subproblemelor, pentru obţinerea soluţiei problemei iniţiale.
Obs: Procesul de descompunere în subprobleme se opreşte când acestea permit o rezolvare directă. Această metodă se aplică în general, pentru prelucrarea vectorilor dar şi a altor tipuri de date.

şir de n numere întregi, folosind metoda Divide et

Impera.
Rezolvare:
Dacă şirul are un singur element, acesta va fi elementul maxim. Pentru un subşir oarecare de cel mult 2 elemente vom avea următoarele etape:
Împărţim şirul iniţial x [ p . . q ] în două subşiruri x [ p . . m] şi x [ m+1 . . q], unde m este mijlocul şirului: m=[(p+q)/2]. Cele două subşiruri pot fi împărţite la rândul lor în alte două şiruri până se ajunge la un subşir de dimensiune 1. Notăm cu x [p . . q] subşirul format din toate elementele şirului dintre x[p] şi x[q].
Se determină recursiv elementul maxim pentru cele două subşiruri (a şi b).
Se combină cele două maxime obţinute pentru aflarea maximului din şirul iniţial.

r21 = 23 r11 = 15

r1 = 15 r2 = 23

r = 23

i,n:integer;

function maxim ( p , q : integer

) : integer;
var m, a, b : integer;
begin
if p < q then begin
m := ( p + q ) div 2;
a := maxim ( p , m );
b := maxim ( m + 1 , q ) ;
if a > b then maxim := a
else maxim := b;
end
else maxim := x [ p ];
end;

to n do
begin
write(‘x[‘,

i ,’]=‘);
readln ( x[i] );
end;
writeln (‘ maximul=‘, maxim ( 1, n ));
readln;
end.

: array [ 1 . . 50 ] of

integer ; i : integer;

function s ( a , b : byte ): longint;
begin
if a > b then s := 0
else if a=b then s := v [ a ]
else s := s ( a , ( a + b ) div 2 ) + s ( ( a + b ) div 2 + 1 , b );
end;

begin
for i := 1 to 20 do v [ i ] := i;
writeln ( s ( 5 , 9 ) );
readln;
end. a) 29 b) 35 c) 45 d) 14

= 10 ?

var n : integer;

function s ( a

, b : integer ) : longint ;
var m : byte;
begin
if a <= b then
begin
m := ( a + b ) div 2;
s := m + s ( a , m-1 ) + s ( m+1 , b );
end
else s := 0;
end;
begin readln(n);
writeln ( s ( 1 , n ) );
end. a) 29 b) 35 c) 41 d) 45