Слайд 2
Аполлоний Пергский (Ἀπολλώνιος ὁ Περγαῖος, Перге, 262 до
н. э. — 190 до н. э.) — древнегреческий математик, один
из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э.
Аполлоний прославился в первую очередь
монографией «Конические сечения» (8 книг),
в которой дал содержательную общую теорию
эллипса, параболы и гиперболы.
Именно Аполлоний предложил общепринятые
названия этих кривых; до него их называли просто
«сечениями конуса». Он ввёл и другие математические
термины, латинские аналоги которых навсегда вошли
в науку, в частности: асимптота, абсцисса, ордината, аппликата
«Парабола» означает приложение или притча.
Долгое время так называли линию среза конуса, пока не появилась квадратичная функция.
Слайд 3
Подумаем, как можно получить массу
информации о коэффициентах
квадратного
трехчлена у =ах2 + bх + с, рассматривая
его
график — параболу.
Сначала напомним хорошо известные факты.
1) Знак коэффициента а (при х2)
показывает направление ветвей
параболы:
а > 0 — ветви вверх;
а < 0 — ветви вниз.
Модуль коэффициента а отвечает за
«крутизну» параболы:
чем больше |a|, тем «круче» парабола.
Слайд 4
2) Коэффициент b (вместе с а) определяет
абсциссу
вершины параболы:
В частности, при а =
1 абсцисса вершины квадратного
трехчлена у = х2 + bх +с равна
При b > 0
вершина расположена
левее оси Оу,
при b < 0 — правее,
при b = 0 — на оси Оу
Слайд 5
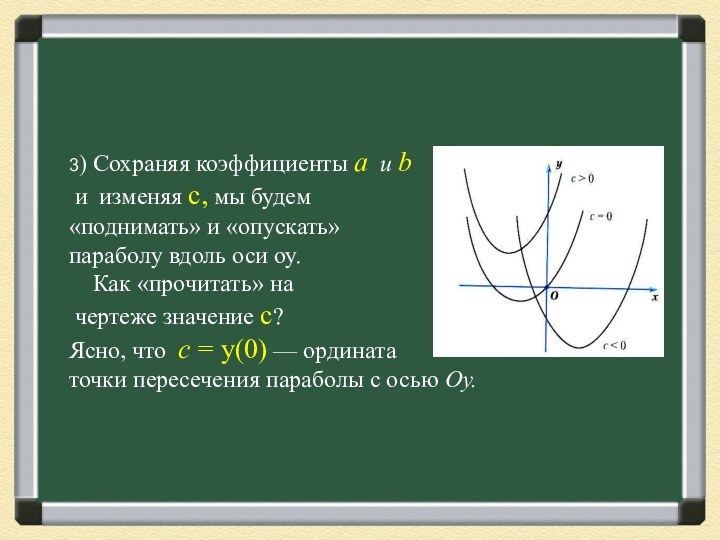
3) Сохраняя коэффициенты a и b
и изменяя
с, мы будем
«поднимать» и «опускать»
параболу вдоль оси
оу.
Как «прочитать» на
чертеже значение с?
Ясно, что с = у(0) — ордината
точки пересечения параболы с осью Оу.
Слайд 6
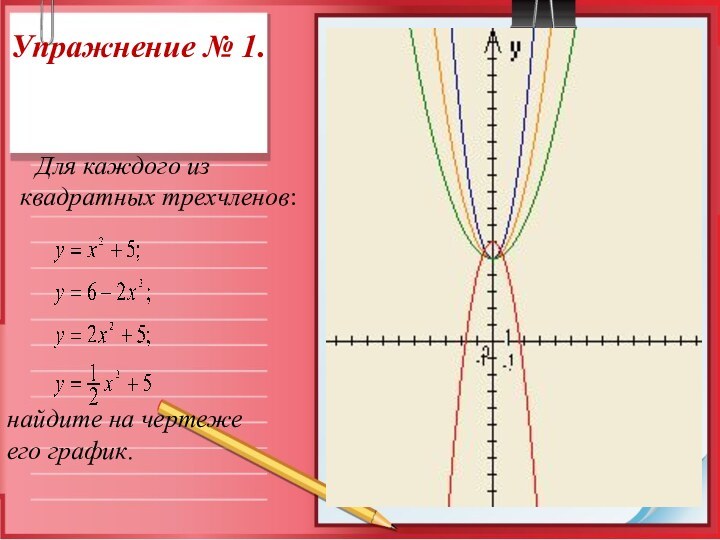
Упражнение № 1.
Для каждого из
квадратных трехчленов:
найдите на чертеже
его график.
Слайд 7
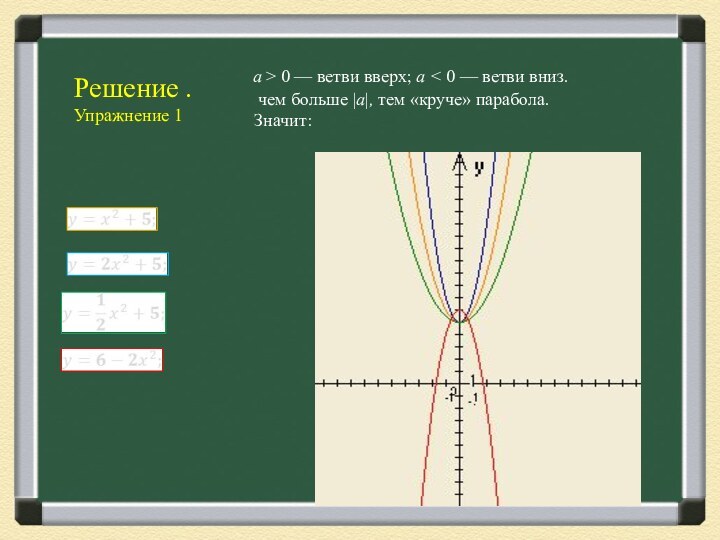
а > 0 — ветви вверх; а
< 0 — ветви вниз.
чем больше |a|, тем
«круче» парабола.
Значит:
Решение .
Упражнение 1
Слайд 8
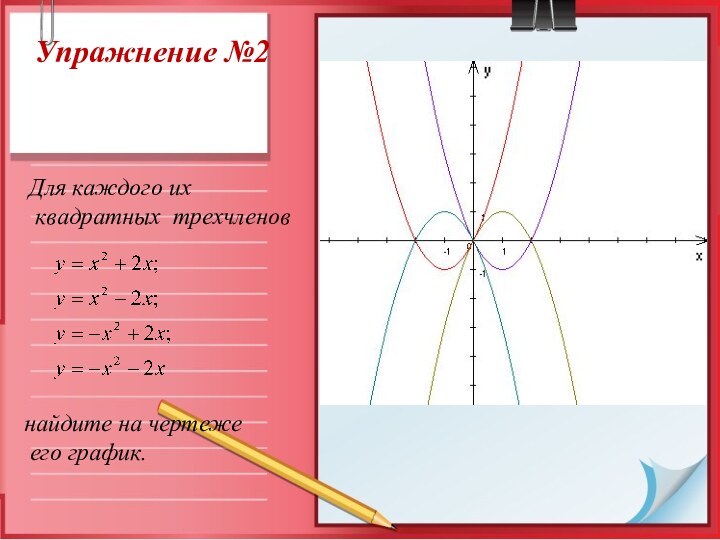
Упражнение №2
Для каждого их
квадратных трехчленов
найдите
на чертеже
его график.
Слайд 9
Решение .
Упражнение 2
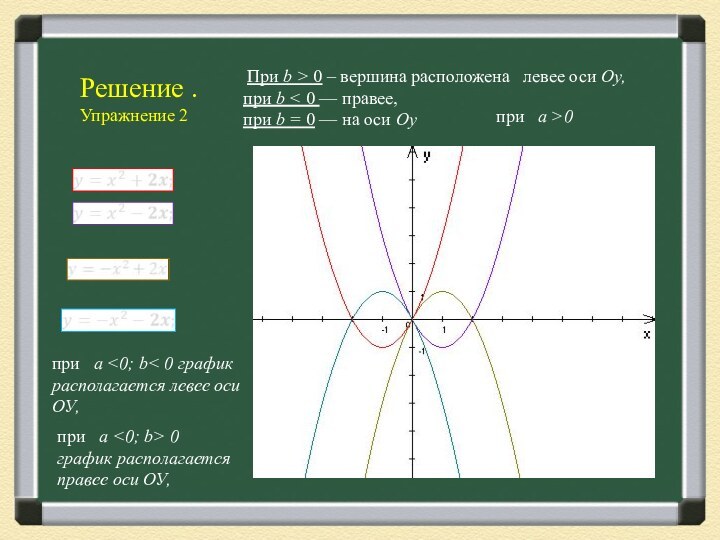
При b > 0 –
вершина расположена левее оси Оу,
при b < 0
— правее,
при b = 0 — на оси Оу
при a >0
при a <0; b< 0 график располагается левее оси ОУ,
при a <0; b> 0 график располагается правее оси ОУ,
Слайд 10
А теперь, когда мы вспомнили как влияют
коэффициенты на построение графика параболы выполним следующие упражнения:
Слайд 11
Упражнение №3
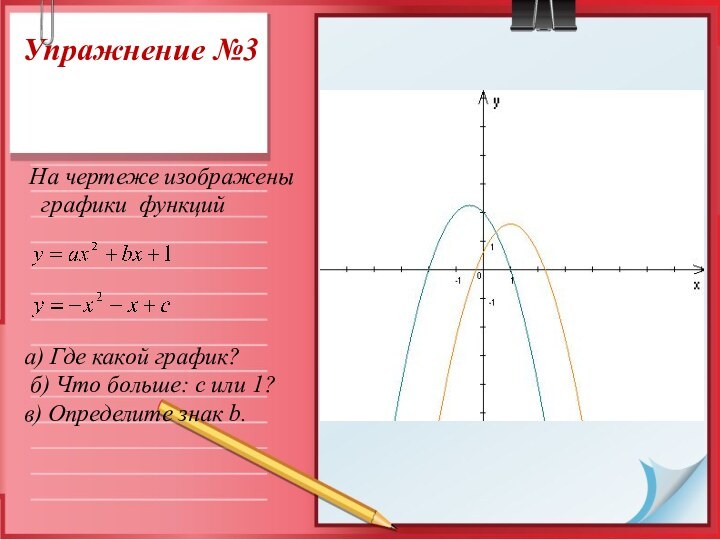
На чертеже изображены
графики функций
а) Где
какой график?
б) Что больше: с или 1?
в) Определите
знак b.
Слайд 12
Решение .
Упражнение 3
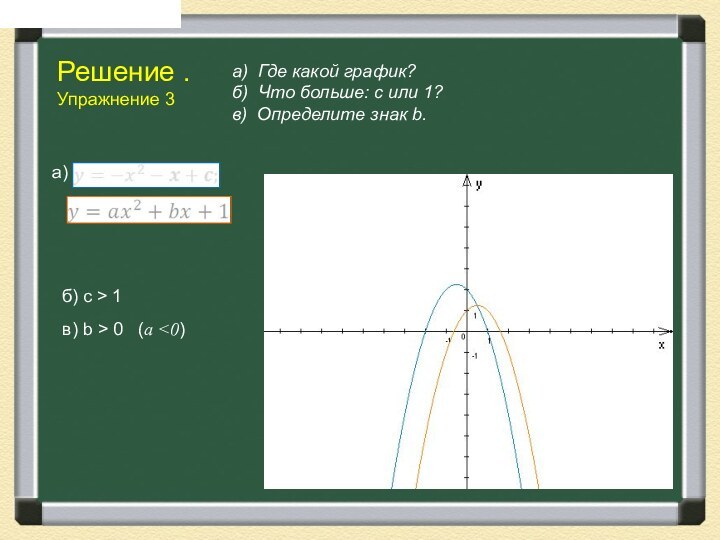
а) Где какой график?
б) Что больше:
с или 1?
в) Определите знак b.
б) с >
1
а)
в) b > 0 (a <0)
Слайд 13
Упражнение №4
На чертеже изображены
графики функций
причем ось оу
, идущая, как
всегда, «снизу вверх»
перпендикулярно оси ох,
стерта.
а) Какая функция имеет
график 1 , а какая -2?
б) Определите знаки c и d .
в) Определите знак b.
Слайд 14
Решение .
Упражнение 4
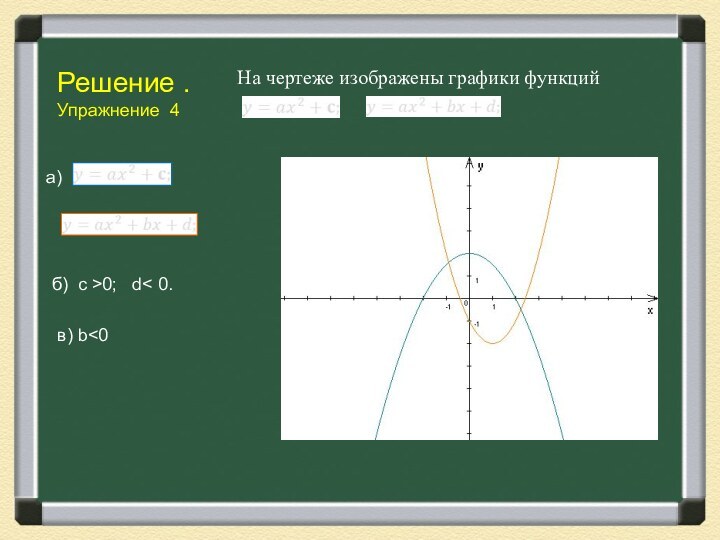
На чертеже изображены графики функций
Слайд 15
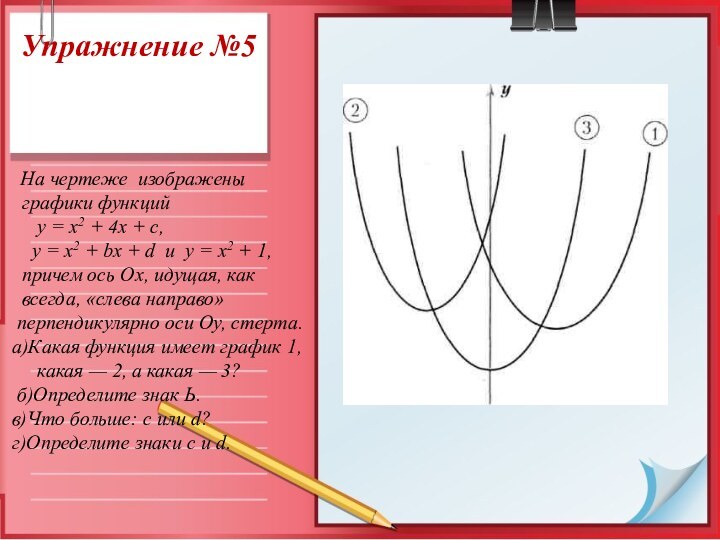
Упражнение №5
На чертеже изображены
графики функций
у = х2 +
4х + с,
у = х2 + bx + d и у = х2 + 1,
причем ось Ох, идущая, как
всегда, «слева направо»
перпендикулярно оси Оу, стерта.
а)Какая функция имеет график 1,
какая — 2, а какая — 3?
б)Определите знак Ь.
в)Что больше: с или d?
г)Определите знаки с и d.
Слайд 16
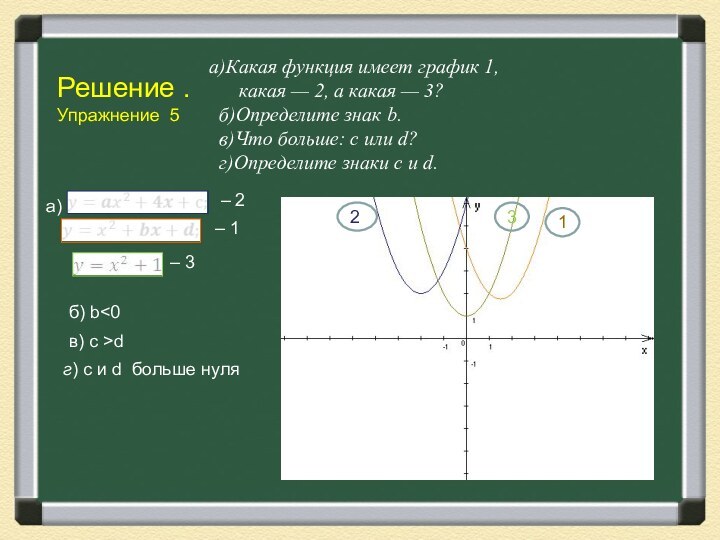
Решение .
Упражнение 5
а)Какая функция имеет график 1,
какая — 2, а какая —
3?
б)Определите знак b.
в)Что больше: с или d?
г)Определите знаки с и d.
а)
– 2
– 3
– 1
б) b<0
в) с >d
г) c и d больше нуля
1
2
3
Слайд 17
Упражнение №6.
На чертеже изображены графики
функций у = ах2
+ х + с и
у = –х2 + bх + 2,
причем оси Оу и Ох,
расположенные стандартным
образом (параллельно краям
листа, Ох — горизонтально
«слева направо»,
Оу — вертикально («снизу
вверх»), стерты.
а) Определите знак b.
б) Определите знак с.
в) Докажите, что
Слайд 18
Решение .
Упражнение 6
а) Определите знак b
б) Определите знак
с.
в) Докажите, что
у =
aх2 + х + с
у = –х2 + b х + 2
1) Ветви параболы у = aх2 + х + с
направлены вверх, значит а>0 ,
знак абсциссы вершины
параболы минус. Тогда , у
параболы у = –х2 + b х + 2
абсцисса тем более
отрицательна. Значит b<0.
2) Ось оу проходит правее
вершины параболы у = aх2 + х + с
значит c<0.
3) Абсцисса вершины параболы
равна ,
у = –х2 + b х + 2
Слайд 19
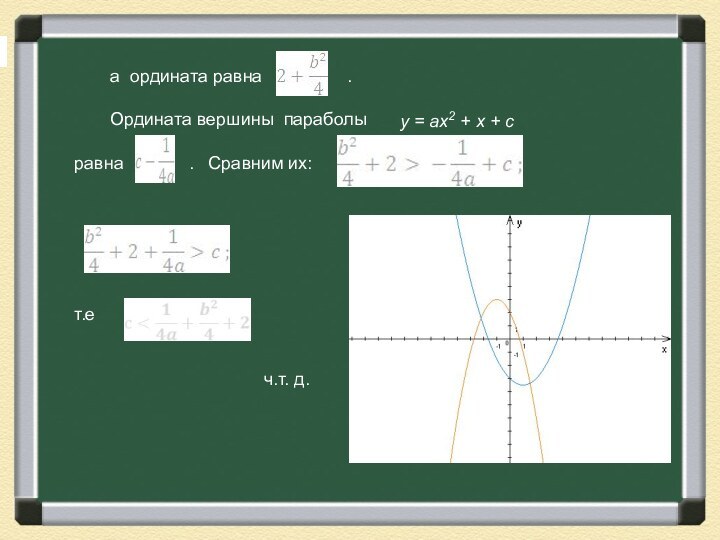
а ордината равна
.
Ордината вершины параболы
равна
. Сравним их:
т.е
ч.т. д.
у = aх2 + х + с
Слайд 20
Решение упражнений основывается на тех фактах, которые мы
знаем о коэффициентах квадратного трехчлена.
Свойства параболы чрезвычайно богаты и
разнообразны, используя их решите следующую задачу.
Слайд 21
Задача.
Известно, что парабола, являющаяся графиком
квадратного трехчлена у = ах2 +
10х + с, не имеет точек в третьей четверти. Какое из следующих утверждений может быть неверным?
(A) а>0
(B) Вершина параболы лежит во второй четверти.
(C) с ≥ 0
(D) c > 0,1
(Е) 1ОО – 4 ас ≤ 0.
Слайд 22
Решение.
Поскольку парабола не имеет точек в
III четверти, то не может быть отрицательным.
Итак, ,следовательно, абсцисса вершины
х0 < 0. То есть вершина не может лежать ни в I, ни в IV четвертях. В III четверти ее нет по условию, значит, она лежит во II четверти.
Итак, парабола обязана иметь такой вид, как показано на рисунке,
поэтому условия А, В и С обязательно выполняются.
Неравенство в Е означает, что дискриминант
неположителен, то есть у квадратного трехчлена
не более одного корня, — это условие тоже
обязательно выполняется. Условие с > 0,1 ни из чего не следует.
Действительно, оно может быть нарушено, например, для параболы
у = х2 + 10х + 0,01, удовлетворяющей условиям задачи.
Ответ: (D).
Слайд 23
Самые близкие родственники параболы – это
окружность, гипербола
и эллипс.
У этого термина существуют и другие значения.
(литература)
Пара́бола «сравнение, сопоставление, подобие, приближение»:
Небольшой рассказ иносказательного характера, имеющий поучительный смысл и особую форму повествования, которое движется как бы по кривой (параболе): начатый с отвлечённых предметов, рассказ постепенно приближается к главной теме, а затем вновь возвращается .