Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Графическое решение задач линейного программирования

Содержание

Задача линейного программирования с двумя неизвестными может быть решена графическиЗамечание:К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2
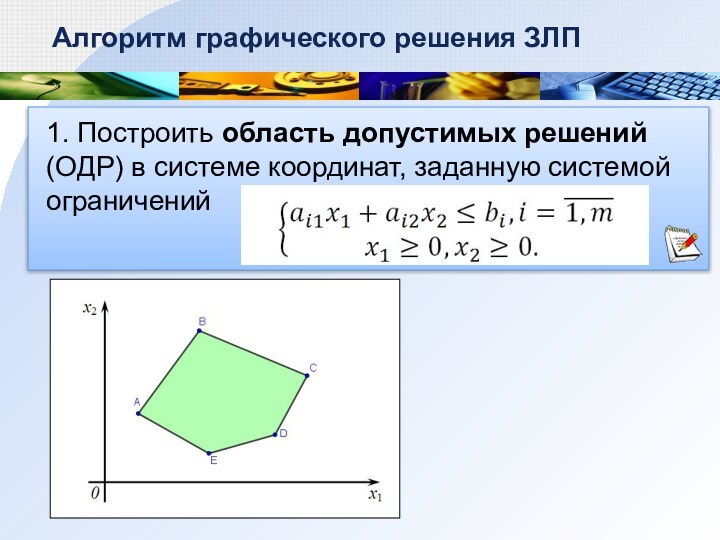
Графическое решение задач линейного программирования Задача линейного программирования с двумя неизвестными может быть решена графическиЗамечание:К такой форме Пусть задача линейного программирования задана в виде: 1. Построить область допустимых решений (ОДР) в системе координат, заданную системой ограничений 2. Построить градиент целевой функции F = с1х1+с2х2 (вектор нормали 3. Построить опорную прямую, перпендикулярную вектору нормали – линию уровня целевой функции 4. Перемещая опорную прямую в направлении вектора нормали, определить «точку входа» и 5. Определить координаты оптимальной точки (точки входа или точки выхода) и найти Минимальное значение целевая функция достигает в точке В: Fmin = F(B) Максимальное Минимальное значение целевая функция достигает в точке E: Fmin = F(E) Максимальное Решить графически ЗЛП Решить графически ЗЛП1. Построим область допустимых решений, заданную системой неравенств (см. 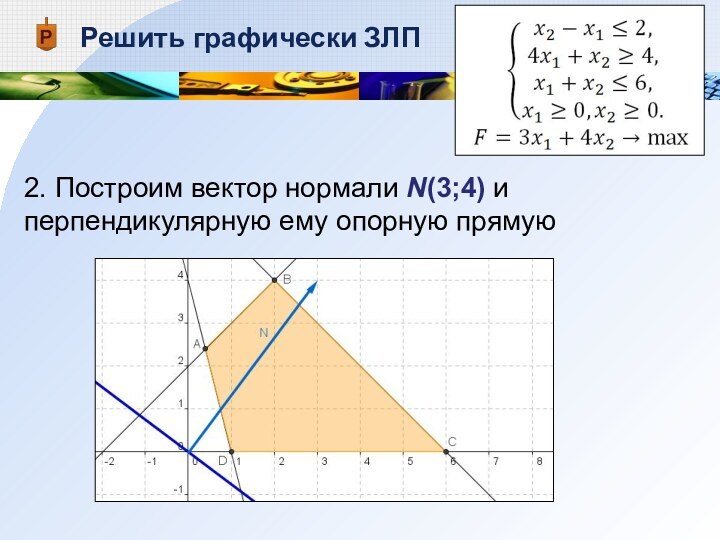презентацию Геометрический смысл линейного неравенства) Решить графически ЗЛП2. Построим вектор нормали N(3;4) и перпендикулярную ему опорную прямую Решить графически ЗЛП3. Перемещаем опорную прямую в направлении вектора нормали и определяем Решить графически ЗЛП4. Найдем координаты точки В, как точки пересечения прямых (1) и (3) Решить графически ЗЛП4. Найдем координаты точки В, как точки пересечения прямых (1) и (3): Решить графически ЗЛП5. Найдем значение целевой функции в точке В Решить графически ЗЛПОтвет: ЛитератураКремер Н.Ш., Путко Б.А. Исследование операций в экономике. - М.: ЮНИТИ, 2003.
Слайды презентации

Слайд 2 Задача линейного программирования с двумя неизвестными может быть

Задача линейного программирования с двумя неизвестными может быть решена графическиЗамечание:К такой

решена графически

Замечание:
К такой форме может быть сведена и каноническая

задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2

Слайд 3
Пусть задача линейного программирования задана в виде:

Пусть задача линейного программирования задана в виде:

Слайд 4
1. Построить область допустимых решений (ОДР) в системе

1. Построить область допустимых решений (ОДР) в системе координат, заданную системой

координат, заданную системой ограничений
Алгоритм графического решения ЗЛП

Слайд 5
2. Построить градиент целевой функции F = с1х1+с2х2

2. Построить градиент целевой функции F = с1х1+с2х2 (вектор нормали к

(вектор нормали к прямой с1х1+с2х2 = F)


Алгоритм графического решения ЗЛП

Слайд 6
3. Построить опорную прямую, перпендикулярную вектору нормали –

3. Построить опорную прямую, перпендикулярную вектору нормали – линию уровня целевой функции Алгоритм графического решения ЗЛП

линию уровня целевой функции
Алгоритм графического решения ЗЛП

Слайд 7
4. Перемещая опорную прямую в направлении вектора нормали,

4. Перемещая опорную прямую в направлении вектора нормали, определить «точку входа»

определить «точку входа» и «точку выхода» (первая встретившаяся опорной

прямой точка из ОДР и последняя встретившаяся опорной прямой точка из ОДР соответственно) В точке входа: F → min В точке выхода: F → max

Алгоритм графического решения ЗЛП

Слайд 8
5. Определить координаты оптимальной точки (точки входа или

5. Определить координаты оптимальной точки (точки входа или точки выхода) и

точки выхода) и найти значение целевой функции в ней
Алгоритм

графического решения ЗЛП

Замечание:
Оптимальная точка является угловой точкой выпуклой области допустимых решений

Слайд 9 Минимальное значение целевая функция достигает в точке В:

Минимальное значение целевая функция достигает в точке В: Fmin = F(B)

Fmin = F(B) Максимальное значение: Fmax = ∞
Частные случаи

Слайд 10 Минимальное значение целевая функция достигает в точке E:

Минимальное значение целевая функция достигает в точке E: Fmin = F(E)

Fmin = F(E) Максимальное значение целевая функция достигает во всех

точках отрезка ВС : Fmin = F(B)= F(C)

Частные случаи

Слайд 11 Решить графически ЗЛП

Решить графически ЗЛП

Слайд 12 Решить графически ЗЛП
1. Построим область допустимых решений, заданную

Решить графически ЗЛП1. Построим область допустимых решений, заданную системой неравенств (см. презентацию Геометрический смысл линейного неравенства)

системой неравенств (см. презентацию Геометрический смысл линейного неравенства)

Слайд 13 Решить графически ЗЛП
2. Построим вектор нормали N(3;4) и

Решить графически ЗЛП2. Построим вектор нормали N(3;4) и перпендикулярную ему опорную прямую

перпендикулярную ему опорную прямую

Слайд 14 Решить графически ЗЛП
3. Перемещаем опорную прямую в направлении

Решить графически ЗЛП3. Перемещаем опорную прямую в направлении вектора нормали и

вектора нормали и определяем «точку выхода»
Файл 04_model_01.ggb
В – точка

выхода


Слайд 15 Решить графически ЗЛП
4. Найдем координаты точки В, как

Решить графически ЗЛП4. Найдем координаты точки В, как точки пересечения прямых (1) и (3)

точки пересечения прямых (1) и (3)

Слайд 16 Решить графически ЗЛП
4. Найдем координаты точки В, как

Решить графически ЗЛП4. Найдем координаты точки В, как точки пересечения прямых (1) и (3):

точки пересечения прямых (1) и (3):

Слайд 17 Решить графически ЗЛП
5. Найдем значение целевой функции в

Решить графически ЗЛП5. Найдем значение целевой функции в точке В

точке В

Слайд 18 Решить графически ЗЛП
Ответ:

Решить графически ЗЛПОтвет:
  • Имя файла: graficheskoe-reshenie-zadach-lineynogo-programmirovaniya.pptx
  • Количество просмотров: 165
  • Количество скачиваний: 0
- Предыдущая Системний червоний вовчак
Следующая - Кутузов и Наполеон

Похожие презентации

Закрепление изученного. Решение задач. презентация к уроку по математике (1 класс) по теме Закрепление изученного. Решение задач. презентация к уроку по математике (1 класс) по теме 158
Внеклассное мероприятие на тему Математический аукцион Внеклассное мероприятие на тему Математический аукцион 120
математика 2 класс презентация урока для интерактивной доски по математике (2 класс) по теме математика 2 класс презентация урока для интерактивной доски по математике (2 класс) по теме 116
НОД по ФЭМП в старшей группе для детей с ТНР презентация к занятию по математике (старшая группа) НОД по ФЭМП в старшей группе для детей с ТНР презентация к занятию по математике (старшая группа) 132
Расчет периметра прямоугольника Расчет периметра прямоугольника 148
m urok47 m urok47 127
Дробь как одна или несколько равных долей Дробь как одна или несколько равных долей 128
Проект по математике Цифра 9 1 класс Проект по математике Цифра 9 1 класс 132
Дидактическая игра Цветочные часы по теме Время + Цветы Дидактическая игра Цветочные часы по теме Время + Цветы 134
Логарифмическая функция Логарифмическая функция 96
Действия с натуральными числами Действия с натуральными числами 115
Конспект занятия с детьми 5-ти лет Царевна Высота. план-конспект занятия по математике (старшая группа) Конспект занятия с детьми 5-ти лет Царевна Высота. план-конспект занятия по математике (старшая группа) 108
Фото-презентация Мой любимый кабинет Фото-презентация Мой любимый кабинет 90
Презентация к уроку. Тема Сложение и вычитание десятичных дробей Презентация к уроку. Тема Сложение и вычитание десятичных дробей 168
Задание В1. Тренажер Задание В1. Тренажер 150
Презентация к уроку математики 6 класс тема: Отношение Презентация к уроку математики 6 класс тема: Отношение 108
Презентация Умножение числа 9 и деление на 9( 2 урок) 2 класс Презентация Умножение числа 9 и деление на 9( 2 урок) 2 класс 165
Статистика и вероятность Статистика и вероятность 97
Кругові діаграми Кругові діаграми 136
trenazhyor slozhenie i vychitanie tryokhznachnykh chisel trenazhyor slozhenie i vychitanie tryokhznachnykh chisel 81
Метод проектов на уроках математики Метод проектов на уроках математики 95
Повторение и закрепление пройденного материала. В гости к Деду Морозу. методическая разработка по математике (2 класс) по теме Повторение и закрепление пройденного материала. В гости к Деду Морозу. методическая разработка по математике (2 класс) по теме 126
Змінні Змінні 182
Симплекс метод Симплекс метод 100
Скалярное произведение векторов Скалярное произведение векторов 129
Презентация : Цвет и форма презентация к уроку по математике (1 класс) Презентация : Цвет и форма презентация к уроку по математике (1 класс) 108
Презентация по математике на тему Числа от 1 до 10 Презентация по математике на тему Числа от 1 до 10 146
правила умножения десятичных дробей правила умножения десятичных дробей 106
Название компонентов и результатов математических действий Название компонентов и результатов математических действий 160
Путешествие к Математическому полюсу. презентация к уроку по математике (4 класс) Путешествие к Математическому полюсу. презентация к уроку по математике (4 класс) 121