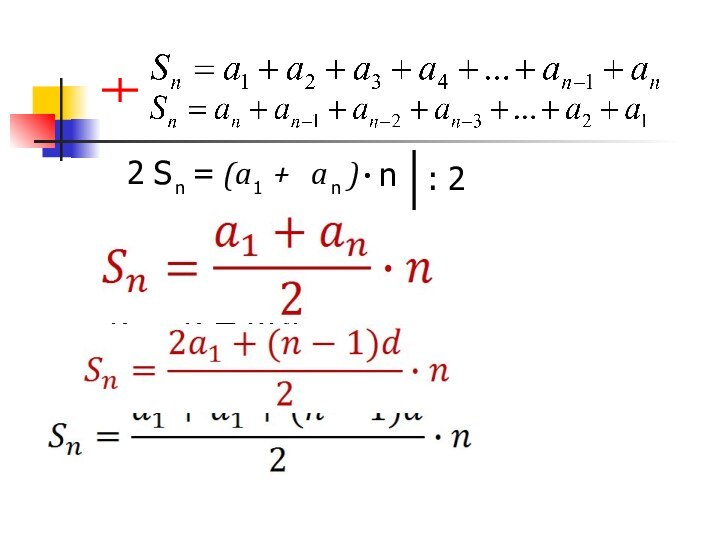Презентация на тему Формула суммы первых n членов арифметической прогрессии

ещё в детстве. По легенде, школьный учитель математики, чтобы

выдающийся немецкий математик, астроном и физик, считается одним из величайших математиков всех времён.
 

«Король математики»

= 5 050

1 + 2 + 3 + 4 + … + 97 + 98 + 99 + 100

Вычислите:

= 101 *

50

1 + 2 +3+…+98+99+100
S=100+99+98+…+ 3 + 2

S=1+2+3+…+98+99+100=5050

1 + 10

2

10

=

5,5;…
Решение
4,
d =
1,5
772,5
Ответ:
772,5

150, которые не делятся на 5.
Задача 19.

Решение

S – искомая сумма;

1; 2; 3; … 150 – арифметическая прогрессия

5; 10; … 150 – арифметическая прогрессия

5;

150;

d =

5;

5n;

5n = 150;

n = 30

= 75 (151 – 31) =

9 000

Ответ:

9 000

чисел, кратных 3,
заключенных в промежутке от

Формула, задающая натуральные числа кратные 3:

Решение

3n

Что об этих числах вы знаете?

: 3

значит, члены последовательности с 34 по 66 удовлетворяют данному
условию.

Последовательность:

102;

105;

108; … ;

198

по определению

арифметическая прогрессия, первый член которой

102;

разность равна

3,

последний член –

198.

Сколько членов в этой прогрессии?

n =

66 – 33 =

33

4950

Ответ:

4 950

больших 50, но меньших
150 и не

Решение

S = 51 +

52 +

53 +

54 +

55 +

56 +

57 +

Исключаем числа:

55;

60;

65; …;

… + 149.

145.

Анализируем

S – искомая сумма,

S =

–

Последовательность чисел: 51; 52; … 149 – арифметическая
прогрессия со знаменателем 1.

900
Последовательность чисел: 55; 60; 65; … ; 145

55,

145,

n =

(n – 1)d

d =

5,

55 + 5(n – 1) = 145

5(n – 1) = 90

n – 1 = 18

n = 19

19

= 1 900

S = 9 900 – 1 900 =

8 000

Ответ: 8 000.